OpenGL ES特效分析 --- 跳动的心

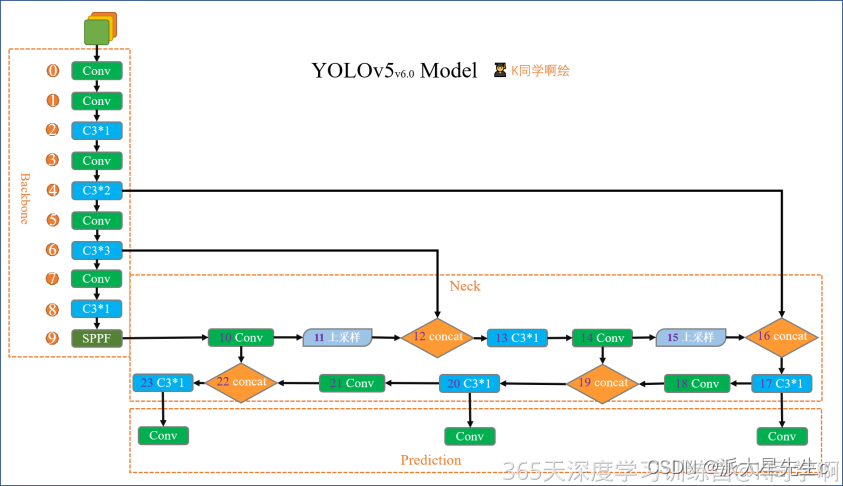
很早之前就见过一个博主发的shader图片，一个跳动的心https://blog.csdn.net/Kennethdroid/article/details/104536532，感觉太好玩了，于是想要分析一下原理，上面的博主也已经做了初步分析，但是对于我这个特效小白来说还是太难，于是就更详细的分析了一遍。
请添加图片描述

把博主对应的代码copy下来，然后一句一句的分析，全部代码如下：

#version 300 es
precision highp float;
layout(location = 0) out vec4 outColor;//输出
uniform float u_time;//时间偏移量
uniform vec2 u_screenSize;//屏幕尺寸
const float PI = 3.141592653;
void main()
{
	// move to center
	vec2 fragCoord = gl_FragCoord.xy;
	vec2 p = (2.0*fragCoord-u_screenSize.xy)/min(u_screenSize.y,u_screenSize.x);
	
	// background color
	vec3 bcol = vec3(1.0,0.8,0.8)*(1.0-0.38*length(p));
	
	// animate
	float tt = u_time;
	float ss = pow(tt,.2)*0.5 + 0.5;
	ss = 1.0 + ss*0.5*sin(tt*6.2831*3.0 + p.y*0.5)*exp(-tt*4.0);
	p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);
	
	// shape
	p.y -= 0.25;
	float a = atan(p.x,p.y) / PI;
	float r = length(p);
	float h = abs(a);
	float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);
	
	// color
	float s = 0.75 + 0.75*p.x;
	s *= 1.0-0.4*r;
	s = 0.3 + 0.7*s;
	s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );
	vec3 hcol = vec3(1.0,0.5*r,0.3)*s;
	
	vec3 col = mix( bcol, hcol, smoothstep( -0.06, 0.06, d-r) );
	
	outColor = vec4(col,1.0);
}

第一步: 分析各个部分代码的功能

第一部分坐标偏移

// move to center
vec2 fragCoord = gl_FragCoord.xy;
vec2 p = (2.0 * fragCoord - u_screenSize.xy) / min(u_screenSize.y,u_screenSize.x);

gl_FragCoord是OpenGL内置的一个变量，表示当前片元相对于窗口所处位置的坐标，只能在Fragment Shader中使用，是vec4类型。详细的介绍请看官网，不过如果是第一次使用的话，不用管这么多的概念，我们这里仅仅是在2D里面使用，可以把gl_FragCoord.xy看成光栅化后的对应实际像素点，大小和glViewport的设置相关。对应的窗口坐标系坐标原点为左下角，左边为X轴正方向，上边为Y轴正方向。
。
上面这段代码是先把这个窗口坐标系经过平移u_screenSize.xy，然后缩放 2 / min(u_screenSize.y,u_screenSize.x)。
坐标p就是gl_FragCoord.xy在新坐标系统的映射。

第二部分背景颜色

// background color
vec3 bcol = vec3(1.0,0.8,0.8)*(1.0-0.38*length(p));

设置整个Shader的背景，这里有风险 1.0-0.38*length(p)可能 < 0，导致颜色绘制不出来，所以应该先判断一下。

第三部分跳动功能

// animate
float tt = u_time;
float ss = pow(tt,.2)*0.5 + 0.5;
ss = 1.0 + ss*0.5*sin(tt*6.2831*3.0 + p.y*0.5)*exp(-tt*4.0);
p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);

根据时间再次变换p的坐标，让心跳起来。

第四部分心形图案

p.y -= 0.25;
float a = atan(p.x,p.y) / PI;
float r = length(p);
float h = abs(a);
float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);

这个部分最关键，绘制心形的图案，其中a，r属于关键信息，h是a的绝对值，d是为了将心扁平化处理进行的进一步操作。

第五部分心形颜色

float s = 0.75 + 0.75*p.x;
s *= 1.0-0.4*r;
s = 0.3 + 0.7*s;
s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );
vec3 hcol = vec3(1.0,0.5*r,0.3)*s;

这里会根据上面计算出来的r 和d，将中间心形的颜色和其余的地方的颜色进行分割，关键函数是OpenGL的内置函数clamp，相当于 min(max(r/d, 0.0), 1.0)。

第六部分合并颜色

vec3 col = mix( bcol, hcol, smoothstep( -0.06, 0.06, d-r) );

将背景色和心的颜色合并，关键函数smoothstep，d-r在[-0.06, 0.06]之间平滑过度，具体效果可以参考https://zhuanlan.zhihu.com/p/157758600。

第二步：拆分核心功能和次要功能，分析核心功能

可以看出，这个shader通过拆分成六部分，生成了最终的颜色，其中有很多优化的地方，但是最核心的只有两个部分，心形图案和心形颜色，所以我们主要分析这两个部分，此外为了正常显示，我们也需要把坐标从左下角移动到屏幕中心，所以也保留第一部分，整体变更为

void main()
{
// move to center
// 第一部分，移动坐标
vec2 fragCoord = gl_FragCoord.xy;
vec2 p = (2.0*fragCoord-u_screenSize.xy)/min(u_screenSize.y,u_screenSize.x);

// shape
// 第四部分，确定心形
p.y -= 0.25;
float a = atan(p.x,p.y) / PI;
float r = length(p);
float h = abs(a);
//float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);
float d = h;//先去掉扁平化处理，先理解整体实现在搞细节

// color
// 第五部分，心形颜色
float s = 0.75 + 0.75; //颜色部分也去掉花里胡哨
//float s = 0.75 + 0.75*p.x;
//s *= 1.0-0.4*r; //颜色部分也去掉花里胡哨
//s = 0.3 + 0.7*s; //颜色部分也去掉花里胡哨
s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );
vec3 hcol = vec3(1.0,0.5*r,0.3)*s;

outColor = vec4(hcol,1.0);
}

效果如下：
请添加图片描述
下面详细分析一下怎么产生的这种效果

vec2 fragCoord = gl_FragCoord.xy;
vec2 p = (2.0*fragCoord-u_screenSize.xy)/min(u_screenSize.y,u_screenSize.x);

// shape
float a = atan(p.x,p.y) / PI;
float r = length(p);
float h = abs(a);
float d = h;

// color
float s = 0.75 + 0.75; //颜色部分也去掉花里胡哨
s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );
vec3 hcol = vec3(1.0,0.5*r,0.3)*s;

先看颜色部分，代码如下，看似花里胡哨，其实总体而言可以理解为
基础颜色 * clamp(r/d, 0.0, 1.0)

float s = 0.75 + 0.75; //颜色部分也去掉花里胡哨
s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0), 0.1 );
vec3 hcol = vec3(1.0,0.5*r,0.3)*s;

所以其中最关键的clamp(r/d, 0.0, 1.0)。
r和d的具体数学公式

float a = atan(p.x,p.y) / PI;
float r = length(p);
float h = abs(a);
float d = h;

整体结合一下，将clamp(r/d, 0.0, 1.0)转换为数学坐标系，整个公式可以表示为：
在这里插入图片描述
这里需要注意的一点是这里的arctan和数学上的arctan不是很一致，一般来说数学上的arctan会返回[−π/2,π/2]，但是这里的是返回 [−π,π]，详情请参考https://registry.khronos.org/OpenGL-Refpages/es3.0/html/atan.xhtml，它会根据(x, y) (其实这里是(y, x))点所在的坐标系，得到具体的角度。于是乎，用desmos模拟一下，得到如下图：
在这里插入图片描述
哎呀妈呀，和实际输出的一样，真的是个心形。
至于为什么有两个，是因为我们用的arctan并不会输出到[−π,π]，而是[−π/2,π/2]，所以为了模拟，有主动加了一个π，然后它里面应该还有一个限制条件，比如实际返回在[−π/2,π/2]之间的时候，y应该大于0，这些我没有在desmos上设置(因为不会~)，所以导致desmos上是两个，但是绘制的时候肯定是一个。
这样就解释了如何渲染出一个心形…完美。

然后再在看看颜色：

float s = 0.75 + 0.75; //颜色部分也去掉花里胡哨
s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0), 0.1 );
vec3 hcol = vec3(1.0,0.5*r,0.3)*s;

可以发现，它实际是使用pow( 1.0-clamp(r/d, 0.0, 1.0), 0.1 )来利用clamp的结果的，我们用desmos看一下x的0.1次方的图案，它在靠近0的时候，会有一个突变，所以转换到pow( 1.0-clamp(r/d, 0.0, 1.0), 0.1 )中，在clamp快等于1的时候，会发生一个突变，这样就很好的分隔了心形颜色和心形之外的颜色。
在这里插入图片描述
核心的功能就全部分析完了。

第三步：优化效果添加功能

对比一下预期，我们想要心的上面更巧，下部分更尖，让心更好看，下面蓝线就是我们想要的大概效果。
请添加图片描述
然后看他shape部分的具体实现，如下。对比上面的核心实现，修改了d的实现，变得更加扁平化。

float a = atan(p.x,p.y) / PI;
float r = length(p);
float h = abs(a);
float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);

为了详细了解这个变化，我们继续用desmos看一下变化：
在这里插入图片描述
可以看到，对比单纯的x线，扁平化的线最开始会更大，之后会更小，这样就可以让a（角度）最开始弧度变的更大，到结尾处变得更尖，这块不知道作者是怎么想出来的公式，也不清楚如何用数学公式表达，有知道同学欢迎评论区交流。
请添加图片描述
然后添加背景颜色,就是上面的第二部分和第六部分

//背景颜色
vec3 bcol = vec3(1.0,0.8,0.8)*(1.0-0.38*length(p));

······
//合并颜色
vec3 col = mix( bcol, hcol, smoothstep( -0.06, 0.06, d-r) );

背景颜色距离中心越远，越像黑色。
合并的时候，用smoothstep对画面效果实现从0 到1 的平滑过度，这样在心与背景交界处，就会有一层蒙版似得东西，让边界不在分明。

动画效果就不分析了，相当于改坐标。

整体分析下来，只能说牛逼，编程的尽头果然是数学，完全不知道这是怎么想出来的。