栈和队列：理解与使用

news2024/10/7 7:25:41

目录

栈

顺序栈结构

链式栈结构

中缀表达式和后缀表达式

顺序栈四则运算

链式栈四则运算

队列

顺序队列结构

链式队列结构

总结

栈和队列是计算机科学中常见的数据结构，它们都是一种线性数据结构，可以对元素进行快速的插入、删除和查找操作。栈和队列都可以用于各种不同的应用场景，不过它们的使用方式和特点有所不同。

栈

首先，让我们来了解一下栈的概念。栈是一种具有“后进先出”（Last In First Out，LIFO）特性的数据结构，如图：

 

只有栈顶元素是可以访问的。新加入的元素会直接放在栈顶，而每次需要访问栈元素时，都会从栈顶开始弹出元素。栈常用于实现函数调用、表达式求值、括号匹配等场景。通常使用 push() 方法将一个元素压入栈中，使用 pop() 方法将栈顶元素弹出。

栈结构包括两类：顺序栈结构和链式栈结构。

顺序栈结构

顺序栈结构使用一组地址连续的内存单元依次保存栈中的数据。在程序中，可以定义一个指定大小的结构数组作为栈，定义一个变量top保存栈顶序号，初始为-1表示空栈。顺序栈的定义和常见操作及代码如下：

#include <stdio.h>
#include <stdlib.h>

typedef struct {
    char *data;
    int top;
    int maxSize;
} Stack;

// 初始化栈
void initStack(Stack *stack, int maxSize) {
    stack->data = (char *)malloc(sizeof(char) * maxSize);
    stack->top = -1;
    stack->maxSize = maxSize;
}

// 判断栈是否为空
int isEmpty(Stack *stack) {
    return stack->top == -1;
}

// 判断栈是否已满
int isFull(Stack *stack) {
    return stack->top == stack->maxSize;
}

// 入栈
void push(Stack *stack, char element) {
    if (isFull(stack)) {
        printf("栈已满，无法入栈！\n");
        return;
    }
    stack->data[++stack->top] = element;
}

// 出栈
char pop(Stack *stack) {
    if (isEmpty(stack)) {
        printf("栈已空，无法出栈！\n");
        return 0;
    }
    return stack->data[stack->top--];
}

// 读取栈顶元素
char peek(Stack *stack) {
    if (isEmpty(stack)) {
        printf("栈已空，无法读取栈顶元素！\n");
        return 0;
    }
    return stack->data[stack->top];
}

// 清空栈
void clear(Stack *stack) {
    stack->top = -1;
}

// 销毁栈
void destroy(Stack *stack) {
    free(stack->data);
    stack->data = NULL;
    stack->top = -1;
    stack->maxSize = 0;
}

链式栈结构

链式栈结构使用链表保存栈元素值，链表头部为栈顶，链表尾部为栈底。链式栈的定义和常见操作及代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define DATA_SIZE 10

// 链式栈结点结构
typedef struct Node {
    char data[DATA_SIZE];
    struct Node *next;
} Node, *LinkedStack;

// 初始化栈
void initStack(LinkedStack *top) {
    *top = NULL;
}

// 判断栈是否为空
int isEmpty(LinkedStack *top) {
    return *top == NULL;
}

// 入栈
void push(LinkedStack *top, char *data) {
    //printf("push: %s ", data);
    Node *node = (Node *)malloc(sizeof(Node));
    strcpy(node->data, data);
    node->next = *top;
    *top = node;
}

// 出栈
void pop(LinkedStack *top, char *data) {
    if (isEmpty(top)) {
        printf("栈已空，无法出栈！\n");
        return;
    }
    Node *node = *top;
    *top = node->next;
    strcpy(data, node->data);
    //printf("pop: %s ", data);
    free(node);
}

// 读取栈顶元素
char* peek(LinkedStack *top) {
    if (isEmpty(top)) {
        printf("栈已空，无法读取栈顶元素！\n");
        return NULL;
    }
    return (*top)->data;
}

// 清空栈
void clear(LinkedStack *top) {
    while (!isEmpty(top)) {
        Node *node = *top;
        *top = node->next;
        free(node);
    }
}

// 销毁栈
void destroy(LinkedStack *top) {
    clear(top);
}

// 打印栈
void print(LinkedStack *top) {
    if (isEmpty(top)) {
        printf("栈已空，无法打印！\n");
        return;
    }
    printf("栈中元素：");
    Node *node = *top;
    while (node != NULL) {
        printf("%s ", node->data);
        node = node->next;
    }
    printf("\n");
}

中缀表达式和后缀表达式

前提提到栈可以用于实现表达式求值，在展示这个案例前，我们先了解一下表达式求值的应用过程。我们平时使用的表达式如“2*(5-1)”是中缀表达式，使用括号来明确运算符的优先级和结合性。后缀表达式（也称为逆波兰表达式），是一种将运算符放置在操作数之后的表示方法，将前面的中缀表达式转换为后缀表达式就是“251-*”。将中缀表达式转换为后缀表达式，可以使表达式更容易计算，而不需要考虑括号和运算符优先级。将中缀表达式 "2*(5-1)" 转换为后缀表达式的过程如下：

  1.  从左到右遍历中缀表达式 "2*(5-1)"；
  2. 遇到操作数 2，将其添加到后缀表达式列表中；
  3. 遇到运算符 *，将其入栈；
  4. 遇到左括号 (，将其入栈；
  5. 遇到操作数 5，将其添加到后缀表达式列表中；
  6. 遇到运算符 -，与栈顶运算符 * 比较，栈顶优先级较低，将 - 入栈（如果栈顶运算符优先级高，则弹出并添加到后缀表达式列表中）。
  7. 遇到操作数 1，将其添加到后缀表达式列表中；
  8. 遇到右括号 )，将栈顶的运算符 - * 依次弹出并添加到后缀表达式列表中，直到遇到左括号 ( 时停止，左括号丢弃；
  9. 中缀表达式遍历完成后，如果栈中还有剩余运算符，则将栈中剩余的运算符依次弹出并添加到后缀表达式列表中。

处理后缀表达式求值的过程则相对简单，因为不需要考虑括号和运算符优先级：

  1. 从左到右遍历后缀表达式中的每个元素；
  2. 如果遇到操作数，将其压入栈中；
  3. 如果遇到运算符，从栈中弹出 2 个操作数，根据运算符进行计算，并将结果压入栈中；
  4. 重复步骤 2 和步骤 3，直到遍历完整个后缀表达式。
  5. 最后，栈中将只剩下一个元素，即为最终的计算结果。

顺序栈四则运算

以下为使用顺序栈结构进行四则运算的例子：

#define MAX_SIZE 100

// 判断是否为运算符
int isOperator(char c) {
    return c == '+' || c == '-' || c == '*' || c == '/';
}

// 判断运算符优先级
int priority(char c) {
    if (c == '+' || c == '-') {
        return 1;
    } else if (c == '*' || c == '/') {
        return 2;
    }
    return 0;
}

// 中缀表达式转后缀表达式
void infixToPostfix(char *infix, char *postfix) {
    Stack stack;
    initStack(&stack, strlen(infix));
    int i = 0, j = 0;
    while (infix[i] != '\0') {
        // 如果是负数，补0变成0-某数
        if (infix[i] == '-' && (i == 0 || infix[i - 1] == '(')) {
            postfix[j++] = '0';
        }

        if (infix[i] == '(') {
            // 如果是左括号，直接入栈
            push(&stack, infix[i]);
        } else if (infix[i] == ')') {
            // 如果是右括号，弹出栈中的元素放入后缀表达式中，直到遇到左括号
            while (peek(&stack) != '(') {
                postfix[j++] = pop(&stack);
            }
            // 弹出左括号，但不放入后缀表达式中
            pop(&stack);
        } else if (isOperator(infix[i])) {
            // 如果是运算符，弹出栈中优先级大于等于当前运算符的元素放入后缀表达式中
            while (!isEmpty(&stack) && priority(peek(&stack)) >= priority(infix[i])) {
                postfix[j++] = pop(&stack);
            }
            // 当前运算符入栈
            push(&stack, infix[i]);
        } else {
            postfix[j++] = infix[i];
        }
        i++;
    }
    // 将栈中剩余的元素放入后缀表达式中
    while (!isEmpty(&stack)) {
        postfix[j++] = pop(&stack);
    }
    postfix[j] = '\0';
    destroy(&stack);
}

// 计算后缀表达式
int calculate(char *postfix) {
    Stack stack;
    initStack(&stack, strlen(postfix));
    int i = 0;
    while (postfix[i] != '\0') {
        if (isOperator(postfix[i])) {
            // 如果是运算符，弹出栈中的两个元素进行运算，将结果入栈
            int a = pop(&stack) - '0';
            int b = pop(&stack) - '0';
            int result;
            switch (postfix[i]) {
                case '+':
                    result = b + a;
                    break;
                case '-':
                    result = b - a;
                    break;
                case '*':
                    result = b * a;
                    break;
                case '/':
                    result = b / a;
                    break;
            }
            push(&stack, result + '0');
        } else {
            push(&stack, postfix[i]);
        }
        i++;
    }
    int result = pop(&stack) - '0';
    destroy(&stack);
    return result;
}

int main() {
    char infix[MAX_SIZE];
    printf("请输入中缀表达式：");
    scanf("%s", infix);
    printf("中缀表达式：%s\n", infix);
    char postfix[strlen(infix)];
    infixToPostfix(infix, postfix);
    printf("后缀表达式：%s\n", postfix);
    printf("计算结果：%d\n", calculate(postfix));
    return 0;
}

链式栈四则运算

以下为使用链式栈结构进行四则运算的例子：

#include <string.h>
#include "LinkedStack.c"
#define MAX_SIZE 100

// 判断是否为运算符
int isOperator(char *str) {
    if (strlen(str) > 1) {
        return 0;
    }
    char c = str[0];
    return c == '+' || c == '-' || c == '*' || c == '/';
}

// 判断运算符优先级
int priority(char *str) {
    char c = str[0];
    if (c == '+' || c == '-') {
        return 1;
    } else if (c == '*' || c == '/') {
        return 2;
    }
    return 0;
}

// 拼接字符
void append(char *str, char c) {
    int len = strlen(str);
    str[len] = c;
    str[len + 1] = '\0';
}

// 字符拷贝
void set(char *str, char c) {
    str[0] = c;
    str[1] = '\0';
}

// 中缀表达式转后缀表达式
int infixToPostfix(char *infix, char postfix[][DATA_SIZE]) {
    LinkedStack stack;
    initStack(&stack);
    int i = 0, j = 0, isOperand = 0;
    char data[DATA_SIZE], oper[1];
    while (infix[i] != '\0') {
        set(oper, infix[i]); //当前操作符/操作数
        // 如果是负数
        if (infix[i] == '-' && (i == 0 || infix[i - 1] == '(')) {
            set(postfix[j++], '-');
            isOperand = 1;
        } else {
            if (infix[i] == '(') {
                // 如果是左括号，直接入栈
                isOperand = 0;
                set(data, infix[i]);
                push(&stack, data);
            } else if (infix[i] == ')') {
                // 如果是右括号，弹出栈中的元素放入后缀表达式中，直到遇到左括号
                isOperand = 0;
                while (peek(&stack)[0] != '(') {
                    pop(&stack, data);
                    strcpy(postfix[j++], data);
                }
                // 弹出左括号，但不放入后缀表达式中
                pop(&stack, data);
            } else if (isOperator(oper)) {
                // 如果是运算符，弹出栈中优先级大于等于当前运算符的元素放入后缀表达式中
                isOperand = 0;
                while (!isEmpty(&stack) && priority(peek(&stack)) >= priority(&infix[i])) {
                    pop(&stack, data);
                    strcpy(postfix[j++], data);
                }
                // 当前运算符入栈
                set(data, infix[i]);
                push(&stack, data);
            } else {
                if (isOperand) {
                    // 该数字是前面的一部分，拼接到后缀表达式最后一个数字中
                    append(postfix[j - 1], infix[i]);
                } else {
                    // 该数字是一个新的数字，直接放到后缀表达式中
                    set(postfix[j++], infix[i]);
                    isOperand = 1;
                }
            }
        }
        i++;
    }
    // 将栈中剩余的元素放入后缀表达式中
    while (!isEmpty(&stack)) {
        pop(&stack, data);
        strcpy(postfix[j++], data);
    }
    postfix[j][0] = '\0';
    destroy(&stack);
    return j;
}

// 计算后缀表达式
int calculate(char postfix[][DATA_SIZE], int size) {
    LinkedStack stack;
    initStack(&stack);
    char data[DATA_SIZE];
    for (int i = 0; i < size; i++) {
        if (isOperator(postfix[i])) {
            // 如果是运算符，弹出栈中的两个元素进行运算，将结果入栈
            pop(&stack, data);
            int a = atoi(data);
            pop(&stack, data);
            int b = atoi(data);
            int result;
            switch (postfix[i][0]) {
                case '+':
                    result = b + a;
                    break;
                case '-':
                    result = b - a;
                    break;
                case '*':
                    result = b * a;
                    break;
                case '/':
                    result = b / a;
                    break;
            }
            itoa(result, data, 10);
            push(&stack, data);
        } else {
            push(&stack, postfix[i]);
        }
    }
    pop(&stack, data);
    destroy(&stack);
    return atoi(data);
}

int main() {
    char infix[MAX_SIZE];
    printf("请输入中缀表达式：");
    scanf("%s", infix);
    printf("中缀表达式：%s\n", infix);
    char postfix[strlen(infix)][DATA_SIZE];
    int len = infixToPostfix(infix, postfix); //有负数的情况下，len会比实际的多1

    // 打印后缀表达式
    printf("后缀表达式(%d)：", len);
    for (int i = 0; i < len; i++) {
        printf(" %s", postfix[i]);
    }
    printf("\n");

    printf("计算结果：%d\n", calculate(postfix, len));
    return 0;
}

大家可以比较上述两个例子，除了所使用的栈结构不同，还有什么差异？

队列

接下来，我们来了解一下队列的概念。队列是一种具有“先进先出”（First In First Out，FIFO）特性的数据结构，如图：

 

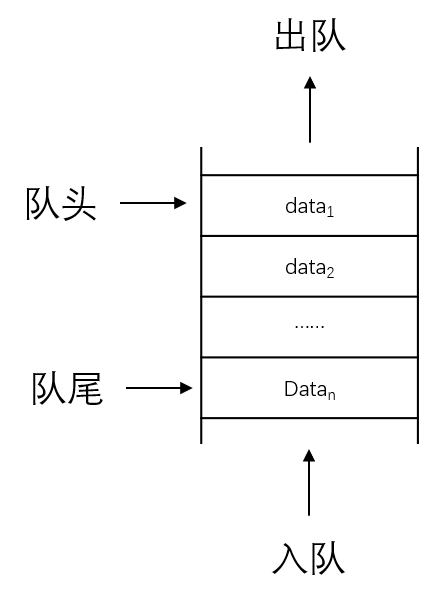
新加入的元素会先放在队尾，而每次需要访问队列元素时，都会从队头开始取出元素，因此队列的操作是双向的。队列常用于实现任务调度、缓冲区管理、广度优先搜索等场景。

队列结构也包括两类：顺序队列结构和链式队列结构。

顺序队列结构

顺序队列结构使用一组地址连续的内存单元依次保存队列中的数据。在程序中，可以定义一个指定大小的结构数组作为队列。

链式队列结构

链式队列结构使用链表保存队列元素值，在链表一端只能进行取出/删除操作，称为队头，在链表的另一端只能进行插入操作，称为队尾。链式队列的常见操作及代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define DATA_SIZE 10

// 链式队列结点结构
typedef struct Node {
    char data[DATA_SIZE];
    struct Node *next;
} Node;

// 链式队列结构
typedef struct LinkedQueue {
    Node *front;
    Node *rear;
} LinkedQueue;

// 初始化队列
void initQueue(LinkedQueue *queue) {
    queue->front = NULL;
    queue->rear = NULL;
}

// 判断队列是否为空
int isEmpty(LinkedQueue *queue) {
    return queue->front == NULL;
}

// 入队
void enqueue(LinkedQueue *queue, char *data) {
    printf("enqueue: %s\n", data);
    Node *node = (Node *)malloc(sizeof(Node));
    strcpy(node->data, data);
    node->next = NULL;
    if (isEmpty(queue)) {
        queue->front = node;
        queue->rear = node;
    } else {
        queue->rear->next = node;
        queue->rear = node;
    }
}

// 出队
void dequeue(LinkedQueue *queue, char *data) {
    if (isEmpty(queue)) {
        printf("队列已空，无法出队！\n");
        return;
    }
    printf("dequeue: %s\n", data);
    Node *node = queue->front;
    queue->front = node->next;
    strcpy(data, node->data);
    free(node);
}

// 读取队头元素
char* peek(LinkedQueue *queue) {
    if (isEmpty(queue)) {
        printf("队列已空，无法读取队头元素！\n");
        return NULL;
    }
    return queue->front->data;
}

// 清空队列
void clear(LinkedQueue *queue) {
    Node *p, *node = queue->front;
    while (p = node) {
        free(p);
        node = node->next;
    }
    queue->front = NULL;
    queue->rear = NULL;
}

总结

需要注意的是，虽然栈和队列都可以用于各种不同的应用场景，但是在使用时需要注意一些细节问题。栈是一种后进先出（LIFO）的数据结构，数据项按照后进先出的顺序存储和访问。最后进入栈的元素是第一个被访问和移除的元素。队列是一种先进先出（FIFO）的数据结构，数据项按照先进先出的顺序存储和访问。最先进入队列的元素是第一个被访问和移除的元素。

栈和队列是计算机科学中重要的数据结构之一，它们都有着广泛的应用场景。了解栈和队列的概念以及使用方法可以帮助我们更好地理解和使用这些数据结构。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/517767.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

00后工资太低，现在转行数据分析还能就业吗？，求大佬指点！

00后工资太低，现在转行数据分析还能就业吗？，求大佬指点！

当然可以就业&#xff0c;只要专业技能过关。IT是靠技术吃饭的行业&#xff0c;没有复杂的人际关系和面子工程&#xff0c;相对其他行业要纯粹一些。当然&#xff0c;如果你技术不过关&#xff0c;或者跟不上技术更新发展速度&#xff0c;淘汰也是必然的&#xff0c;IT行业不能…
阅读更多...
听我一句劝，千万别去外包，两年外包生涯做完，感觉自己废了一半....

听我一句劝，千万别去外包，两年外包生涯做完，感觉自己废了一半....

先说一下自己的情况。大专生&#xff0c;18年通过校招进入湖南某软件公司&#xff0c;干了接近5年的点点点&#xff0c;今年年上旬&#xff0c;感觉自己不能够在这样下去了&#xff0c;长时间呆在一个舒适的环境会让一个人堕落&#xff01;而我已经在一个企业干了五年的功能测试…
阅读更多...
前端开发和测试的新伙伴：Requestly，让你事半功倍！

前端开发和测试的新伙伴：Requestly，让你事半功倍！

目录 引言 痛点 前端测试 后端测试 曾使用的应对措施 Charles Chrome 插件 实现mock工具 Requestly Requestly的功能 流量捕捉方式 请求的修改 响应的修改 请求响应录制 我对Requestly的应用 总结 引言 想必每个前端开发和测试的小伙伴都曾经历过不断地切换页…
阅读更多...
CV界的chatgpt出现——Segment Anything能分割万物

CV界的chatgpt出现——Segment Anything能分割万物

目录 一、前言&#xff08;1&#xff09;弱人工智能&#xff08;Weak AI&#xff09;&#xff08;2&#xff09;强人工智能&#xff08;General AI&#xff09;&#xff08;3&#xff09;超人工智能&#xff08;Super AI&#xff09; 二、SAM的一些介绍2.1 模型的结构是什么&am…
阅读更多...
React动态路由配置

React动态路由配置

目录 项目初始化 模块创建 统一导出 全局模块配置选项 核心代码 使用及效果展示 博文适用于react-router v6及以上&#xff0c;其中还有很多值得改进的地方 最近学习react的过程中&#xff0c;思考怎样实现动态路由的配置(最终实现从页面配置最终动态从数据库加载上线模…
阅读更多...
C++解析JSON JSONCPP库的使用

C++解析JSON JSONCPP库的使用

首先去GitHub下载JSONCPP的源码&#xff1a; JSonCpp的源码 解压后得到&#xff1a;jsoncpp-master 文件夹 需要的是&#xff1a;jsoncpp-master\src\lib_json 目录下的所有文件和 jsoncpp-master\include\json 目录下的所有文件&#xff0c;在MFC工程目录下新建两个文件夹或…
阅读更多...
承诺协议：定义 构造

承诺协议：定义 构造

文章目录 安全性定义方案构造基于 OWP 存在性基于 DL 假设基于 OWF 存在性基于 DDH 假设 总结 安全性定义 承诺协议&#xff08;Commitment Scheme&#xff09;是一个两阶段的两方协议。一方是承诺者&#xff08;Committer&#xff09; C C C&#xff0c;另一方是接收者&#…
阅读更多...
网络安全怎么学？

网络安全怎么学？

一、怎么入门&#xff1f; 这个 Web 安全学习路线&#xff0c;整体大概半年左右&#xff0c;具体视每个人的情况而定。 &#xff08;上传一直很模糊&#xff0c;所以就没有展开了&#xff0c;需要高清版的可以在下面领取&#xff09; &#x1f449; 【一学习路线高清版一】&a…
阅读更多...
WiFi（Wireless Fidelity）基础（八）

WiFi（Wireless Fidelity）基础（八）

目录 一、基本介绍&#xff08;Introduction&#xff09; 二、进化发展&#xff08;Evolution&#xff09; 三、PHY帧&#xff08;&#xff08;PHY Frame &#xff09; 四、MAC帧&#xff08;MAC Frame &#xff09; 五、协议&#xff08;Protocol&#xff09; 六、安全&#x…
阅读更多...
AndroidStudio-学习笔记之多级目录功能的设计与开发

AndroidStudio-学习笔记之多级目录功能的设计与开发

多级目录功能的设计与开发 演示效果需求描述开发预计前端后端 前端开发多级目录的UI小框架前端xml前端代码---本地demo版前端代码---服务器版逻辑说明 后端开发表设计书写接口 演示效果 需求描述 根据需求&#xff0c;为用户展示多级目录(目前设计的为4级目录)&#xff0c;并在…
阅读更多...
Win10笔记本无法正常启动代码0xc0000001解决方法

Win10笔记本无法正常启动代码0xc0000001解决方法

Win10笔记本无法正常启动代码0xc0000001解决方法。最近不少的用户在笔记本电脑安装Win10系统使用时&#xff0c;出现了蓝屏的情况&#xff0c;电脑显示错误代码0xc0000001无法启动到桌面使用。那么这个情况怎么去进行问题的解决呢&#xff1f;来看看以下的解决方法吧。 准备工作…
阅读更多...
OpenCL编程指南-4.1OpenCL C编程

OpenCL编程指南-4.1OpenCL C编程

使用OpenCL C编写数据并行内核 OpenCL中的数据并行性表述为一个N维计算域&#xff0c;其中N1、2或3。N-D域定义了可以并行执行的工作项的总数。下面通过一个简单的例子来了解如何用OpenCL C编写一个数据并行内核&#xff0c;将两个浮点数数组相加。这个代码的串行版本求和时需…
阅读更多...
在windows上通过QEMU快速上手RT-thread smart

在windows上通过QEMU快速上手RT-thread smart

参考链接 官方文档 资料下载 env-windows-v1.3.5.7z userapps 注意事项 通过QEMU仿真不同的平台&#xff0c;使用到的交叉编译工具也不一样&#xff0c;需要将相应工具的路径添加到系统PATH里&#xff1b;或者通过CMD定位到userapps&#xff0c;运行smart-env.bat xxx&…
阅读更多...
【jvm系列-11】jvm性能调优篇---命令行工具的基本使用

【jvm系列-11】jvm性能调优篇---命令行工具的基本使用

JVM系列整体栏目 内容链接地址【一】初识虚拟机与java虚拟机https://blog.csdn.net/zhenghuishengq/article/details/129544460【二】jvm的类加载子系统以及jclasslib的基本使用https://blog.csdn.net/zhenghuishengq/article/details/129610963【三】运行时私有区域之虚拟机栈…
阅读更多...
智能优化算法——下山单纯型算法

智能优化算法——下山单纯型算法

作者&#xff1a;非妃是公主 专栏&#xff1a;《智能优化算法》 博客地址&#xff1a;https://blog.csdn.net/myf_666 个性签&#xff1a;顺境不惰&#xff0c;逆境不馁&#xff0c;以心制境&#xff0c;万事可成。——曾国藩 文章目录 专栏推荐序一、算法流程1. 反射2. 膨胀…
阅读更多...
马哈鱼SQLFLow数据流生成介绍

马哈鱼SQLFLow数据流生成介绍

马哈鱼数据血缘分析器是当前最流行的数据血缘关系(data lineage)管理工具之一&#xff0c;它是一种通过分析SQL脚本来自动发现数据流向的工具。它通过生成一个简洁的图表来显示数据仓库中表/视图和列之间的数据流。支持超过20种流行的数据库&#xff0c;包括 bigquery, couchba…
阅读更多...
项目风险的4种应对策略及实施条件

项目风险的4种应对策略及实施条件

面对威胁或可能给项目带来消极影响的风险&#xff0c;我们一般采用规避、转移、缓解和接受的应对策略。 一、风险规避 风险规避策略是指项目团队采取行动来消除威胁&#xff0c;或保护项目免受风险影响的应对策略&#xff0c;通常包括改变项目管理计划&#xff0c;以完全消除威…
阅读更多...
super_数学知识(质数筛选和约数学习)lesson08易错题记录

super_数学知识(质数筛选和约数学习)lesson08易错题记录

文章目录 回文质数第n小的质数素数个数 回文质数 先上代码 #include<iostream> #include<vector>//创建动态数组需要的头文件 #include<cstring>//使用memset需要的头文件 using namespace std; vector<int> q; bool arr[10000005]; //埃氏筛法找出所…
阅读更多...
详解软件开发的标准过程(生命周期)：跟着标准搞，设计没烦恼

详解软件开发的标准过程(生命周期)：跟着标准搞，设计没烦恼

目录 一.软件开发的生命周期总括 二.项目架构分类 C/S架构 B/S架构 三.详解软件需求 需求分类 需求获取 需求分析 四.详解面向对象分析&#xff08;OOA&#xff09; 概念理解&#xff1a; 统⼀建模语⾔UML UML的重要组成部分&#xff1a; ⽤例图的元素 识别参与者…
阅读更多...
怎么搭建个人小型渲染农场？搭建渲染农场配置

怎么搭建个人小型渲染农场？搭建渲染农场配置

渲染农场是众多机器组成的渲染集群&#xff0c;通常用来渲染你的单帧效果图或动画项目&#xff0c;我们借助渲染农场的力量&#xff0c;可以满足3D项目交期时间迫在眉睫的需求&#xff0c;当你试着在自己的机器上渲染一个复杂的动画项目时&#xff0c;可能需要几十小时的等待时…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023