回文质数

先上代码

#include<iostream>
#include<vector>//创建动态数组需要的头文件
#include<cstring>//使用memset需要的头文件
using namespace std;
vector<int> q;
bool arr[10000005];
//埃氏筛法找出所有的质数
void is_Prime(int n)
{
	memset(arr, true, sizeof(arr));			
	arr[1] = false;//1不是素数
	for (int i = 2;i * i <= n;i++)
	{
		if (arr[i])	//把所有素数的倍数都不可能是素数	
		{	
			for (int j = 2;j * i <= n;j++)//从i*2开始，然后i*3..
				arr[j * i] = false;
		}
	}
	
}
//判断是否为回文数
bool huiwen(int n){
    int hui[8]={};//最大可能是八位
    for(int i=0;i<8;i++,n/=10){
        hui[7-i]=n%10;//讲该数正序存储到数组当中
    }
    int j;
    q.clear();
    //当该数小于8位时，去掉前面的无用0
    for(j=0;hui[j]==0;j++);
    for(int k=j;k<8;k++){
        q.push_back(hui[k]);//将该数各个位上的数存到q里
    }
    int len=q.size();
    for(int x=0;x<len/2;x++){
        if(q[x]!=q[len-1-x]) return false;
    }
    return true;
}
int main(){
    int a,b;
    cin>>a>>b;
    if(a%2==0)a++;//奇数不可能会是质数
    if(b>=10000000) b=9999999;//10000000之后没有回文数,这样可以降低O
    is_Prime(b);
    //下面这里+=2是因为这样可以直接去掉偶数的判断，偶数不可能是质数
    for(int i=a;i<=b;i+=2){
        if(arr[i]&&huiwen(i)) cout<<i<<endl;
    }
    
}

memset(arr, true, sizeof(arr));	

memset(arr, true, sizeof(arr)) 是一个用于将内存块的值设置为指定值的函数。在这里，它的作用是将数组 arr 的所有元素设置为 true。

具体来说，memset 函数的第一个参数是目标内存块的指针，第二个参数是要设置的值，第三个参数是要设置的内存块的大小。sizeof(arr) 表示数组 arr 的大小（以字节为单位）。

所以，memset(arr, true, sizeof(arr)) 的意思是将数组 arr 的所有元素设置为 true，也就是将所有元素初始化为 true。在这段代码中，它的作用可能是用来初始化布尔数组 arr，确保所有元素的初始值都为 true。

if (a % 2 == 0) a++;

在以上代码中，if (a % 2 == 0) a++; 是为了确保起始数a是奇数。这是因为题目要求在范围 [a, b] 内找到所有回文质数，而回文数一定是个位数为奇数的数字。

通过这个判断，如果 a 是偶数，则将其增加1，使其成为下一个奇数。这样可以确保起始数a是奇数，从而在循环中以步长为2递增，只考虑奇数，避免了对偶数进行不必要的判断。

因为偶数（除了2）一定不是质数，所以在查找回文质数的过程中，我们可以直接从奇数开始遍历，提高效率。

vector<int> q; 

vector q; 是定义了一个名为 q 的整型向量（vector）。这个向量可以存储一组整数，并根据需要动态调整大小。

q.clear(); 

q.clear(); 是向量 q 的成员函数，用于清空向量中的元素。它将向量的大小设置为0，即移除所有元素，使向量为空。

在上述代码中，q 被用作临时存储回文数的容器。在 huiwen() 函数中，回文数的每一位数字被存储在 q 中，然后进行回文数的判断。在每次判断完成后，通过 q.clear() 清空 q，以便存储下一个回文数的数字。这样可以确保每次判断都是基于当前回文数的数字集合，避免与上一次的结果冲突。

q.push_back(s[j]);

q.push_back(s[j]); 是向向量 q 的末尾添加一个新的元素。在这里，s[j] 表示将 s 数组中索引为 j 的元素添加到向量 q 的末尾。

int size = q.size();

q.size() 是返回向量 q 的当前大小（即元素的个数）。在这里，q.size() 用于确定回文数的位数，以便进行回文性检查。

总结：
q.push_back(s[j]); 是向向量 q 添加一个元素。
q.size() 是返回向量 q 的大小（元素个数）。

第n小的质数

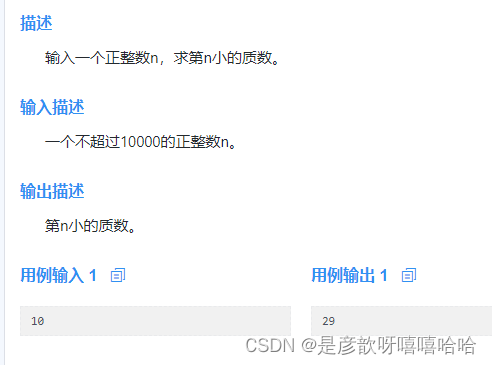
#include<iostream>
using namespace std;

int main() {
    long long int sum = 1, i, j, n;  // 定义变量a、b、c、i、j、n、k，其中n表示要求的第n小的质数
    cin >> n;  // 输入一个正整数n

    if (n == 1)  // 如果n等于1
        cout << 2;  // 输出2，2是第一个质数
    else {
        for (i = 3;; i += 2) {  // 从3开始循环，每次加2，因为偶数（除了2）不可能是质数
            for (j = 3; j < i; j += 2) {  // 内层循环从3开始，每次加2，判断i是否可以被k整除
                if (i % j == 0)  // 如果i能被k整除
                    break;  // 跳出内层循环，说明i不是质数
                if (j * j > i)  // 如果k的平方大于i
                    break;  // 跳出内层循环，说明i是质数
            }
            if (j * j > i)  // 如果k的平方大于i
                sum++;  // 质数计数器a加1
            if (sum == n) {  // 如果质数计数器a等于n
                cout << i;  // 输出第n小的质数i
                return 0;  // 程序结束
            }
        }
    }
    return 0;
}

在质数判断的算法中，当一个数大于其平方根时，它一定不会有除了1和自身以外的因数。

在这段代码中，k * k > i 的条件检查是为了判断是否已经找到了当前数 i 的所有可能因数。在内层循环中，从 k 开始递增，当 k 的平方超过 i 时，就意味着在 k 的范围内已经找不到能整除 i 的因数了。

如果 k * k > i 成立，即 k 的平方大于 i，那么 i 不会被 k 之后的数整除，因此可以确定 i 是一个质数。

素数个数

第一种方法：埃氏筛质数

#include<iostream>
using namespace std;
#define maxn 50000
int prime[maxn];
int main(){
	int n,sum=0;
	cin>>n;
	prime[1]=1;
	for(int i=2;i<maxn;i++){
		if(prime[i]) continue;
		for(int j=i+i;j<maxn;j+=i){
			prime[j]=1;
		}
	}
	for(int i=2;i<=n;i++){
		if(prime[i]==0) sum++;
	}
	cout<<sum;
	return 0;
}

第二种方法：线性筛法
埃筛有个问题数字60，会被质数2、3、5分别标记一下，运行速度会降低一点。如何避免这种情况，如何提高时间效率为O(n)?
将每个合数用它的最小质因数筛除因此每个数只会被标记一次，时间复杂度是O(n)

#include<iostream>
using namespace std;

int prime[50000], p[50000], cnt;
// prime[] - 用于存储数字是否为素数的数组
// p[] - 用于存储素数的数组
// cnt - 计数变量，用于记录素数的个数

int count(int n) {
    prime[1] = 1;
    // 初始化 prime[1] 为 1，因为 1 不是素数

    for (int i = 2; i <= n; i++) {
        if (prime[i] == 0)
            p[++cnt] = i;
        // 如果 prime[i] 为 0，表示 i 是素数，将其存储到 p[] 数组中，并增加计数器

        for (int j = 1; j <= cnt && i * p[j] <= n; j++) {
            prime[i * p[j]] = 1;
            // 将 i * p[j] 标记为非素数，将 prime[i * p[j]] 设为 1

            if (i % p[j] == 0)
                break;
            // 如果 i 可以被 p[j] 整除，无需继续内循环
        }
    }
    return cnt;
    // 返回素数的个数
}

int main() {
    int n;
    cin >> n;
    cout << count(n);
    // 读取输入的 n，调用 count 函数计算素数的个数，并输出结果
}

if (i % p[j] == 0)
     break;
    // 如果 i 可以被 p[j] 整除，无需继续内循环
}

当在内循环中发现 i 可以被 p[j] 整除时，我们可以确定 i 不是一个素数。因为 i 是从小到大遍历的，而 p[j] 是小于或等于 i 的素数。

如果 i 能够被 p[j] 整除，那么它一定也能够被其他比 p[j] 更小的素数整除。如果我们继续在内循环中检查 i 能否被比 p[j] 更大的素数整除，这是多余的，因为我们已经找到了一个能够整除 i 的最小素数 p[j]。

因此，如果 i 能够被 p[j] 整除，我们可以断定 i 不是素数，并且终止内循环，以节省计算时间。这样可以提高算法的效率，避免重复的检查。