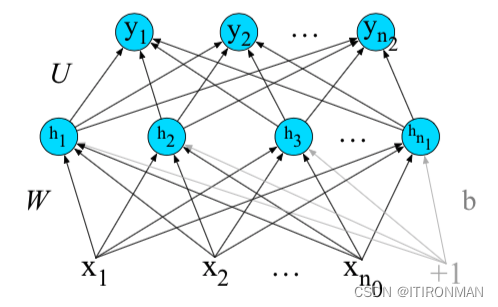
上面这句话很好的解释了一件事,就是“大力出奇迹” ,当神经元的数目足够足够多的时候,机器所能做到的事情就很复杂、很难理解了,这是不是说明chatgpt的成功也是因为大?
现代神经网络是一个由小型计算单元组成的网络,每个计算单元接受一个输入值向量,并产生一个输出值。我们介绍的结构被称为前馈网络,因为计算从一层单元到下一层单元逐层进行。现代神经网络的使用通常被称为深度学习,因为现代网络通常是深度的(有很多层)。神经网络与逻辑回归有许多相同的数学原理。但神经网络是一个比逻辑回归更强大的分类器,事实上,一个最小的神经网络(技术上只有一个“隐藏层”)可以学习任何函数。
神经网络分类器与逻辑回归在另一个方面有所不同。在逻辑回归中,我们通过基于领域知识开发多种丰富的特征模板,将回归分类器应用于许多不同的任务。当使用神经网络时,更常见的做法是避免大多数使用丰富的手工衍生特征,而是构建神经网络,将原始单词作为输入,并学习归纳特征,作为学习分类过程的一部分。深度的网络特别擅长表示学习。因此,深度神经网络是解决大规模问题的合适工具,因为这些问题提供了足够的数据来自动学习特征。也就是说,罗辑回归时代,特征是需要自己人工去找,然后在训练不同特征权重,而到了深度学习时代,特征是需要模型自己去找,省去了人工的麻烦。
1、神经元
神经网络的构建块是一个单独的计算单元。一个单元以一组实数作为输入,对它们进行一些计算,然后产生一个输出。在其核心,神经单元对其输入进行加权和,并在和中添加一个称为偏置项的附加项。给定一组输入x1…Xn,一个单位有一组对应的权重w1…wn和偏置b,所以加权和z可以表示为:
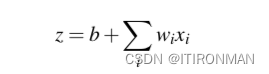
通常用向量表示这个加权和更方便;回想一下线性代数中,向量本质上就是一个数字列表或数组。因此,我们将用权向量w,标量偏置b和输入向量x来表示z,我们将用方便的点积来代替这个和:
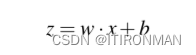
最后,不使用z, 而是对x计算后的线性函数作为输出,神经单元我们将该函数的输出称为单元a的激活值。由于我们只是对单个单元进行建模,因此节点的激活实际上是网络的最终输出,我们通常将其称为y。因此y的值定义为:
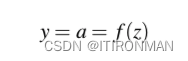
我们将在下面讨论三种流行的非线性函数f (sigmoid, tanh和整流线性ReLU),但从sigmoid函数比较方便 :
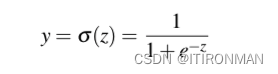
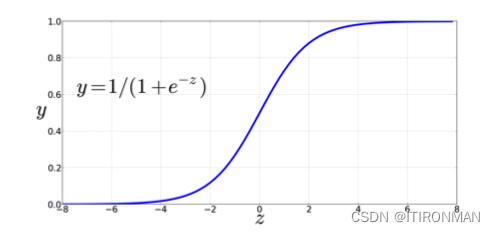
上面是sigmoid函数的曲线,可以看到具备非常好的压缩性能,进一步细化公式:
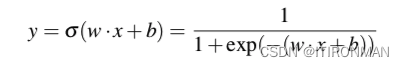
在下图中,3个输入值x1、x2和x3,并计算一个加权和,将每个值乘以一个权重(分别为w1、w2和w3),将它们加到一个偏置项b中,然后将结果和通过sigmoid函数传递,得到一个介于0和1之间的数字 :
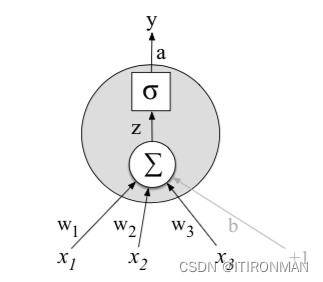

在实践中,sigmoid不常用作激活函数。一个非常相似但几乎总是更好的函数tanh,其范围从-1到+1 。
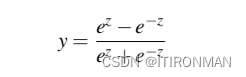
另外,还有relu:
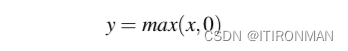

在神经网络的早期历史中,人们意识到神经网络的工作能力,就像启发它们的真实神经元一样,来自于将这些单元组合成更大的网络。
2、神经网络
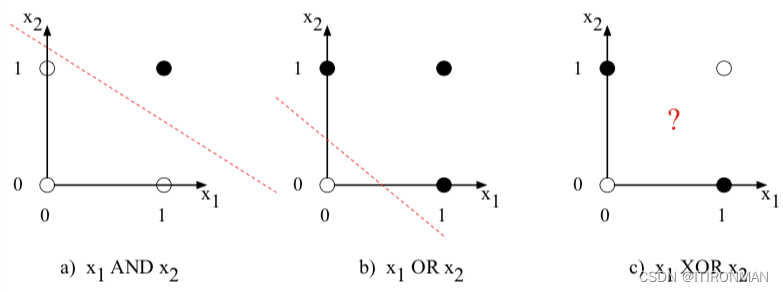
众所周知,一个单一的神经元是无法分割异或问题的(不知道的可以自行搜索)。
虽然异或函数不能由单个感知机计算,但它可以由单元的分层网络计算。但是可以使用两层基于relu的单元来计算异或。中间层(称为h)有两个单位,输出层(称为y)有一个单位。显示了正确计算异或函数的每个ReLU的一组权重和偏置。
让我们看看输入x =[0 0]时会发生什么。如果我们将每个输入值乘以适当的权重和,然后加上偏置b,我们得到向量[0 -1],然后我们应用整流线性变换使h层的输出为[0 0]。现在,我们再次乘以权重,求和,并加上偏差(在本例中为0),结果为0。读者应该通过计算剩余的3个可能的输入对,看到输入[0 1]和[1 0]的结果y值为1,输入[0 0]和[1 1]的结果y值为0。
查看中间结果(两个隐藏节点h0和h1的输出)也很有指导意义。在上一段中,我们展示了输入x =[0 0]的h向量是[0 0]。注意,两个输入点x =[0 1]和x =[10 0]的隐藏表示(XOR输出= 1的两个情况)被合并到单个点h =[10 0]。合并可以很容易地线性分离异或的正负情况。换句话说,我们可以将网络的隐藏层看作是对输入的表示。
3、前反馈神经网络
现在让我们稍微正式地介绍一下最简单的神经网络,前馈网络。前馈网络是一种多层网络,其中单元之间无循环连接;每一层单元的输出被传递给下一层的单元,没有输出被传递回较低的层。神经网络的核心是由隐藏单元组成的隐藏层,每个隐藏单元都是一个神经单元,对其输入进行加权和,然后应用非线性。在标准体系结构中,每一层都是全连接的,这意味着每一层中的每个单元都将前一层中所有单元的输出作为输入,并且来自相邻两层的每一对单元之间都有一个链接。因此,每个隐藏单元对所有输入单元求和。