自相关问题®
文章目录
- 自相关问题(R)
- @[toc]
- 1 什么是自相关
- 2 自相关产生的原因
- 3 自相关的后果
- 4 自相关检验
- 5 自相关补救
- 6 R语言操作
文章目录
- 自相关问题(R)
- @[toc]
- 1 什么是自相关
- 2 自相关产生的原因
- 3 自相关的后果
- 4 自相关检验
- 5 自相关补救
- 6 R语言操作
1 什么是自相关
经典普通最小二乘法估计的假设之一是扰动项不存在自相关,即对于
∀
i
≠
j
\forall i\ne j
∀i=j,都有
C
o
v
(
μ
i
,
μ
j
)
=
0
Cov(\mu_i,\mu_j)=0
Cov(μi,μj)=0
不成立。如何扰动项之间存在相关性,则采用OLS得到的估计量不是最佳的。一个二阶自相关问题用数学模型可以表示为
{
y
t
=
α
+
β
x
t
+
μ
t
μ
t
=
ρ
1
μ
t
−
1
+
ρ
2
μ
t
−
2
+
v
t
E
(
v
t
)
=
0
;
V
a
r
(
v
t
)
=
σ
2
\left\{\begin{array}{l} y_t = \alpha+\beta x_t+\mu_t\\ \mu_t = \rho_1\mu_{t-1}+\rho_2\mu_{t-2}+v_t\\ E(v_t) = 0;Var(v_t) = \sigma^2 \end{array}\right.
⎩
⎨
⎧yt=α+βxt+μtμt=ρ1μt−1+ρ2μt−2+vtE(vt)=0;Var(vt)=σ2
上述模型表明,自相关问题体现在扰动项上,即扰动项是一个自回归AR过程,而线性模型
y
t
=
α
+
β
x
t
+
μ
t
y_t = \alpha+\beta x_t+\mu_t
yt=α+βxt+μt的扰动项存在AR过程则该模型存在自相关问题。将扰动项AR代入线性模型得到
y
t
=
α
+
β
x
t
+
ρ
1
μ
t
−
1
+
ρ
2
μ
t
−
2
+
v
t
E
(
v
t
)
=
0
;
V
a
r
(
v
t
)
=
σ
2
y_t = \alpha+\beta x_t+\rho_1\mu_{t-1}+\rho_2\mu_{t-2}+v_t\\ E(v_t) = 0;Var(v_t) = \sigma^2
yt=α+βxt+ρ1μt−1+ρ2μt−2+vtE(vt)=0;Var(vt)=σ2
2 自相关产生的原因
- 经济系统的惯性(通胀)
- 经济活动滞后效应(蛛网现象)
- 模型设定问题
3 自相关的后果
- 无偏性:无偏性推导过程中没有用到关于扰动项的方差协方差矩阵,因此不会影响估计量的无偏性。
- 最佳性:估计量方差推导使用了扰动项的方差协方差矩阵,由于扰动项不再满足球形扰动假设,最佳性不再满足。
- t统计量:t统计量是估计量与相应标准误的比值,分母不再是最小的,则t统计量减小,可能影响显著性,以及区间估计和假设检验。
4 自相关检验
对于一阶自相关问题,常用的检验方法是DW检验,其中
D
W
=
2
−
2
ρ
^
DW = 2-2\hat\rho
DW=2−2ρ^
其中
ρ
^
\hat\rho
ρ^ 是扰动项一阶自相关系数。根据
D
W
DW
DW统计量与相应的临界值比较,可以判断该模型是否存在自相关问题,以及正或负自相关问题。但DW检验存在如下问题:
- DW检验存在统计值盲区,在该盲区内无法判断是否存在自相关
- DW检验仅适合一阶自相关检验,对高阶自相关失效
- DW检验的模型不能以被解释变量滞后项为自变量
- DW检验需要大样本作支撑,以提高检验所需的自由度
- 需要先验证据论证存在一阶自相关问题,而非高阶自相关问题
对于高阶自相关问题,可以采用BG检验(T.S.Breusch and L.G.Godfrey test)方法,也称为拉格朗日(LM)检验方法。操作步骤是
1、使用OLS估计得到残差
2、用残差对所有自变量以及自变量的滞后项作回归,滞后阶数可以由从小到大或从大到小的序贯原则确定,也可使用AI或BIC准则确定。
3、若残差滞后项对应自相关估计量显著,表明存在自相关,阶数即显著的自相关系数对应的最大滞后项。
其他一些方法,如利用残差对其滞后项作回归,滞后阶数与上面BG检验类似,或者检验残差及滞后项的相关系数,或画散点图作经验分析。
5 自相关补救
补救方法可使用广义差分法(是可行加权最小二乘法(FGLS)特殊情况),OLS+异方差自相关稳健标准误(Nwey-West)。下面是广义差分法的操作步骤。对于一阶自相关问题
{
Y
t
=
β
1
+
β
2
X
t
+
μ
t
μ
t
=
ρ
μ
t
−
1
+
v
t
\left\{\begin{array}{l} Y_t = \beta_1+\beta_2 X_t+\mu_t\\ \mu_t = \rho\mu_{t-1}+v_t\\ \end{array}\right.
{Yt=β1+β2Xt+μtμt=ρμt−1+vt
将线性模型滞后一期
Y
t
−
1
=
β
1
+
β
2
X
t
−
1
+
u
t
−
1
Y_{t-1}=\beta_{1}+\beta_{2} X_{t-1}+u_{t-1}
Yt−1=β1+β2Xt−1+ut−1
两边同时乘以
ρ
\rho
ρ得
ρ
Y
t
−
1
=
ρ
β
1
+
ρ
β
2
X
t
+
ρ
u
t
−
1
\rho Y_{t-1}=\rho \beta_{1}+\rho \beta_{2} X_{t}+\rho u_{t-1}
ρYt−1=ρβ1+ρβ2Xt+ρut−1
本期减滞后期
Y
t
−
ρ
Y
t
−
1
=
β
1
(
1
−
ρ
)
+
β
2
(
X
t
−
ρ
X
t
−
1
)
+
u
t
−
ρ
u
t
−
1
Y_{t}-\rho Y_{t-1}=\beta_{1}(1-\rho)+\beta_{2}\left(X_{t}-\rho X_{t-1}\right)+u_{t}-\rho u_{t-1}
Yt−ρYt−1=β1(1−ρ)+β2(Xt−ρXt−1)+ut−ρut−1
此时新扰动项为
v
t
v_t
vt满足经典假设。令
Y
t
∗
=
Y
t
−
ρ
Y
t
−
1
,
X
t
∗
=
X
t
−
ρ
X
t
−
1
,
β
1
∗
=
β
1
(
1
−
ρ
)
Y_{t}^{*}=Y_{t}-\rho Y_{t-1}, X_{t}^{*}=X_{t}-\rho X_{t-1}, \quad \beta_{1}^{*}=\beta_{1}(1-\rho)
Yt∗=Yt−ρYt−1,Xt∗=Xt−ρXt−1,β1∗=β1(1−ρ),则新估计方程为
Y
t
∗
=
β
1
∗
+
β
2
X
t
∗
+
v
t
Y_{t}^{*}=\beta_{1}^{*}+\beta_{2} X_{t}^{*}+v_{t}
Yt∗=β1∗+β2Xt∗+vt
可以发现,通过广义差分得到估计系数
β
2
\beta_2
β2未发生改变,即新方程的斜率就是原方程自变量对因变量的边际效应。
6 R语言操作
下面通过数据模拟方式对以上关键步骤进行模拟。数据模拟过程也是对自相关问题数据生成过程的理解。扰动项的AR(2)数据过程为
rm(list = ls())
library(lmtest)
set.seed(10)
N = 1000
# 扰动项自相关生成
err = rnorm(N,0,1)
# AR(2)过程
e = filter(err,c(-0.6,0.2),method="recursive")
par(mfrow = c(1,1))
plot(e)
OLS_e = lm(e[1:(N-2)]~1+e[2:(N-1)]+e[3:N])
summary(OLS_e)
# Call:
# lm(formula = e[1:(N - 2)] ~ 1 + e[2:(N - 1)] + e[3:N])
#
# Residuals:
# Min 1Q Median 3Q Max
# -3.462 -0.673 -0.026 0.660 3.014
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.0109 0.0314 0.35 0.73
# e[2:(N - 1)] -0.5472 0.0309 -17.72 < 2e-16 ***
# e[3:N] 0.2275 0.0309 7.37 3.6e-13 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.992 on 995 degrees of freedom
# Multiple R-squared: 0.528, Adjusted R-squared: 0.527
# F-statistic: 555 on 2 and 995 DF, p-value: <2e-16
利用filter函数即可生成AR(2),回归的自相关系数与设定的自相关系数非常接近。下面产生自变量和因变量
# DGP-xy
x = rnorm(N,1,2)
y = 1 +0.5*x + e
OLS = lm(y~1 + x)
summary(OLS)
结果如下:
# Call:
# lm(formula = y ~ 1 + x)
#
# Residuals:
# Min 1Q Median 3Q Max
# -4.974 -1.028 0.015 0.991 3.913
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.0166 0.0508 20.0 <2e-16 ***
# x 0.4917 0.0218 22.5 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 1.44 on 998 degrees of freedom
# Multiple R-squared: 0.337, Adjusted R-squared: 0.336
# F-statistic: 507 on 1 and 998 DF, p-value: <2e-16
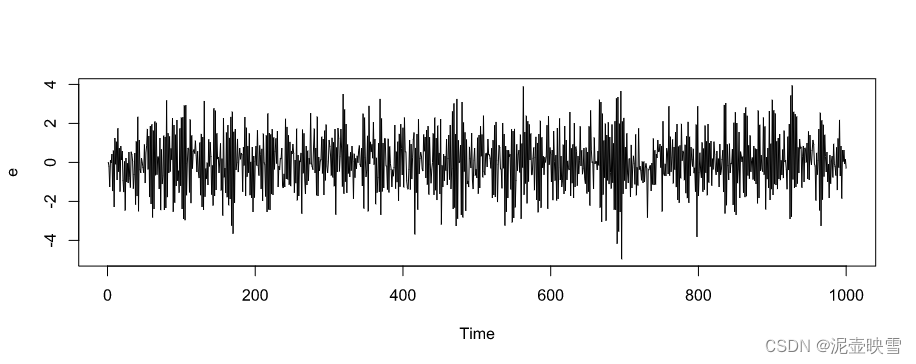
一个自相关问题的线性模型就生成好了,开始进行检验。第一种方法采用DW检验
# 自相关检验
dwtest(y ~ x)
Durbin-Watson test
data: y ~ x
DW = 3.41, p-value = 1
alternative hypothesis: true autocorrelation is greater than 0
p值竟然为1,选择不拒绝原假设是有问题的,因为DW检验仅适合一阶自相关问题。本问题是二阶自相关,检验失效。采用BG检验方法,先进性三阶自相关检验
# BG检验
bg3 = bgtest(y ~ 1+x,order = 3)
coeftest(bg3)
# z test of coefficients:
#
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -0.0298 0.0350 -0.85 0.394
# x 0.0290 0.0151 1.93 0.054 .
# lag(resid)_1 -0.5498 0.0316 -17.38 < 2e-16 ***
# lag(resid)_2 0.2393 0.0354 6.76 1.4e-11 ***
# lag(resid)_3 0.0158 0.0317 0.50 0.617
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
结果表明三阶滞后并不显著,但一二阶非常显著,考虑使用将参数order 取值为2
bg2 = bgtest(y ~ 1+x,order = 2)
coeftest(bg2)
# z test of coefficients:
#
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -0.0296 0.0350 -0.85 0.398
# x 0.0288 0.0151 1.91 0.056 .
# lag(resid)_1 -0.5462 0.0308 -17.74 < 2e-16 ***
# lag(resid)_2 0.2306 0.0308 7.48 7.5e-14 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
故原模型存在二阶自相关。再使用散点图,分析本期残差与向前一期和二期的走势
par(mfrow = c(1,2))
r = as.numeric(OLS$res)
plot(r[1:(N-1)],r[2:N],xlab = expression(e[t]),
ylab = expression(e[t-1]))
plot(r[1:(N-2)],r[3:N],xlab = expression(e[t]),
ylab = expression(e[t-2]))
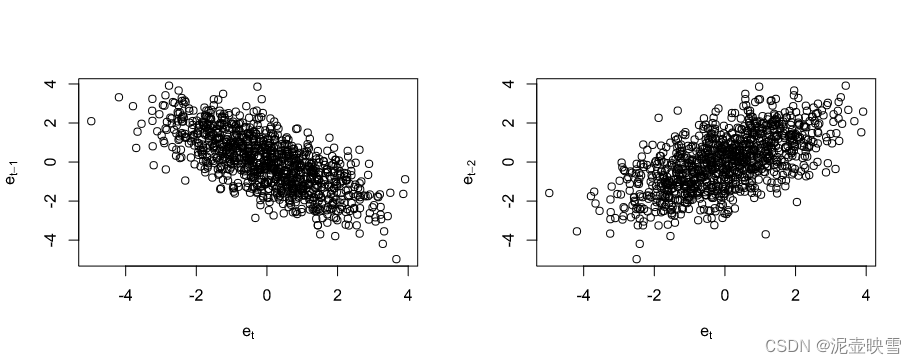
可以发现残差滞后一期与本期存在负相关,与滞后两期存在正相关。使用回归检验方法,还能粗略获取相关系数
# 回归检验法
OLS_r = lm(r[1:(N-2)]~1+r[2:(N-1)]+r[3:N])
# OLS_r = lm(r[1:(N-3)]~1+r[2:(N-2)]+r[3:(N-1)]+r[4:N])
summary(OLS_r)
# Call:
# lm(formula = r[1:(N - 2)] ~ 1 + r[2:(N - 1)] + r[3:N])
#
# Residuals:
# Min 1Q Median 3Q Max
# -3.470 -0.671 -0.026 0.666 2.961
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.000287 0.031451 0.01 0.99
# r[2:(N - 1)] -0.546255 0.030869 -17.70 < 2e-16 ***
# r[3:N] 0.227704 0.030869 7.38 3.4e-13 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.994 on 995 degrees of freedom
# Multiple R-squared: 0.526, Adjusted R-squared: 0.525
# F-statistic: 553 on 2 and 995 DF, p-value: <2e-16
结果表明一阶自相关系数为 ρ 1 = − 0.546 \rho_1 = -0.546 ρ1=−0.546, ρ 2 = 0.227 \rho_2 = 0.227 ρ2=0.227。与最初设定的-0.6和0.2较为接近。检验结果除了DW外,都表明存在二阶自相关,下面使用广义差分法进行补救。
# BG检验表明存在AR(2),粗略估计一阶自相关系数和二阶自相关系数
bg2 = bgtest(y ~ 1+x,order = 2)
rho1 = as.numeric(bg2$coefficients[3])
rho2 = as.numeric(bg2$coefficients[4])
# 采用广义差分法
new.y = y[1:(N-2)] - rho1*y[2:(N-1)] - rho2*y[3:N]
new.x = x[1:(N-2)] - rho1*x[2:(N-1)] - rho2*x[3:N]
OLS2 = lm(new.y~new.x)
# 广义差分不改变斜率,只改变截距
summary(OLS2)
# Call:
# lm(formula = new.y ~ new.x)
#
# Residuals:
# Min 1Q Median 3Q Max
# -3.443 -0.681 -0.009 0.657 3.160
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.2950 0.0360 36.0 <2e-16 ***
# new.x 0.5232 0.0131 40.1 <2e-16 ***
# ---
# Signif. codes:
# 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.99 on 996 degrees of freedom
# Multiple R-squared: 0.617, Adjusted R-squared: 0.617
# F-statistic: 1.61e+03 on 1 and 996 DF, p-value: <2e-16
再次进行BG检验
bgtest(OLS2,order = 2)
# Breusch-Godfrey test for serial correlation of order
# up to 2
#
# data: OLS2
# LM test = 0.342, df = 2, p-value = 0.84
表明不存在二阶自相关问题。前面的自相关系数是通过BG辅助回归获取,现在使用相关系数获取
# 对于AR(2)过程,简单相关系数过于粗略
rho1 = cor(r[1:(N-1)],r[2:N])
rho2 = cor(r[1:(N-2)],r[3:N])
new.y = y[1:(N-2)] - rho1*y[2:(N-1)] - rho2*y[3:N]
new.x = x[1:(N-2)] - rho1*x[2:(N-1)] - rho2*x[3:N]
OLS3 = lm(new.y~new.x)
# Call:
# lm(formula = new.y ~ new.x)
#
# Residuals:
# Min 1Q Median 3Q Max
# -3.493 -0.894 -0.026 0.876 4.470
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.0776 0.0420 25.6 <2e-16 ***
# new.x 0.5218 0.0137 38.2 <2e-16 ***
# ---
# Signif. codes:
# 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 1.24 on 996 degrees of freedom
# Multiple R-squared: 0.594, Adjusted R-squared: 0.594
# F-statistic: 1.46e+03 on 1 and 996 DF, p-value: <2e-16
使用相关系数提取,残差依然存在AR(2)
bgtest(OLS3,order = 2)
# Breusch-Godfrey test for serial correlation of order
# up to 2
#
# data: OLS3
# LM test = 51.6, df = 2, p-value = 6.2e-12
利用回归方法获取自相关系数
OLS.rho = lm(r[1:(N-2)]~r[2:(N-1)]+r[3:N])
rho1 = as.numeric(OLS.rho$coefficients[2])
rho2 = as.numeric(OLS.rho$coefficients[3])
new.y = y[1:(N-2)] - rho1*y[2:(N-1)] - rho2*y[3:N]
new.x = x[1:(N-2)] - rho1*x[2:(N-1)] - rho2*x[3:N]
OLS4 = lm(new.y~new.x)
summary(OLS4)
# Call:
# lm(formula = new.y ~ new.x)
#
# Residuals:
# Min 1Q Median 3Q Max
# -3.448 -0.679 -0.008 0.659 3.160
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.2979 0.0360 36 <2e-16 ***
# new.x 0.5232 0.0131 40 <2e-16 ***
# ---
# Signif. codes:
# 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.99 on 996 degrees of freedom
# Multiple R-squared: 0.617, Adjusted R-squared: 0.616
# F-statistic: 1.6e+03 on 1 and 996 DF, p-value: <2e-16
使用BG进行阶自相关检验
bgtest(OLS4,order = 2)
# Breusch-Godfrey test for serial correlation of order
# up to 2
#
# data: OLS4
# LM test = 0.442, df = 2, p-value = 0.8
结果表明不存在二阶自相关。最后使用科克伦-奥克特迭代法,安装包里面帮助文档显示只适合一阶自相关问题,高阶并不适合。使用orcutt方法进行迭代
# install.packages("orcutt")
# 仅能解决残差AR(1)过程
library(orcutt)
OLS5 = cochrane.orcutt(OLS)
summary(OLS5)
# Call:
# lm(formula = y ~ 1 + x)
#
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.9843 0.0230 42.8 <2e-16 ***
# x 0.5232 0.0128 40.8 <2e-16 ***
# ---
# Signif. codes:
# 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 1.0163 on 997 degrees of freedom
# Multiple R-squared: 0.6248 , Adjusted R-squared: 0.6244
# F-statistic: 1660.3 on 1 and 997 DF, p-value: < 1.862e-214
#
# Durbin-Watson statistic
# (original): 3.41457 , p-value: 1e+00
# (transformed): 1.67709 , p-value: 1.522e-07
结果显示,原方程的DW统计量由3.41变为1.67,但结果依然存在一阶自相关。由于本问题是二阶自相关,因此该方法失效。
bgtest(OLS5,order = 2)
# Breusch-Godfrey test for serial correlation of order
# up to 2
#
# data: OLS5
# LM test = 42.8, df = 2, p-value = 5.1e-10
下面为以上所有补救策略的输出。由于自相关不影响无偏性,回归系数基本不受影响,差异在于估计量的标准误上。其中采用BG检验(2)和回归检验(4)提取的自相关系数进行广义差分补救不存在自相关问题,采用相关系数方法未能补救成功。并且回归结果(2)(4)的估计量标准误都比其他估计结果低。
library(stargazer)
stargazer(OLS,OLS2,OLS3,OLS4,OLS5,type = "text",
keep=c("x","new.x","Constant"),
keep.stat=c("n","adj.rsq"))
=========================================================
Dependent variable:
--------------------------------------------
y new.y y
(1) (2) (3) (4) (5)
---------------------------------------------------------
x 0.492*** 0.523***
(0.022) (0.013)
new.x 0.523*** 0.522*** 0.523***
(0.013) (0.014) (0.013)
Constant 1.017*** 1.295*** 1.078*** 1.298*** 0.984***
(0.051) (0.036) (0.042) (0.036) (0.023)
---------------------------------------------------------
Observations 1,000 998 998 998 1,000
Adjusted R2 0.336 0.617 0.594 0.616
=========================================================
Note: *p<0.1; **p<0.05; ***p<0.01