手把手教你实现红黑树

news2025/11/4 20:31:48

目录

一.红黑树介绍与优势

二.红黑树的特性

①所有节点不是黑色就是红色

②根节点为黑色

③红色节点的左右孩子节点必须为黑色

④每一条路径均含有相同的黑色节点数

⑤叶子节点为黑色

三.红黑树实现原理

（一）.插入节点颜色选择

（二）.插入后，父节点是黑色

（三）.插入后，父节点是红色

（四）.叔叔节点为红色

①父节点、叔叔节点变黑，祖父节点变红

②以祖父节点为“新插入节点”继续向上判断

（五）.叔叔节点为黑色、没有叔叔节点

①当前节点为父节点左子树，且在根节点左侧

②当前节点为父节点右子树，且在根节点右侧

③当前节点为父节点右子树，且在根节点左侧

④当前节点为父节点左子树，且在根节点右侧

四.思维导图

五.实现代码

一.红黑树介绍与优势

有兴趣的小伙伴可以先看看这篇文章：手把手教你实现AVL树、平衡二叉树

红黑树是在1972年由Rudolf Bayer发明的。

其特点是从根到叶子节点的所有路径中，最长路径不大于最短路径的2倍。

可以说红黑树是AVL树的plus版，因此，红黑树查找时间与AVL树相同，都为O(log N)。

同时，红黑树没有做到AVL树那种绝对平衡，因此其旋转次数少于AVL树。当数据量大时，其效率要优于AVL树。

正因如此，在实际应用中往往采取红黑树而非AVL树。

二.红黑树的特性

可以说，红黑树的特性正是它的精华与结构依据。因此，想要学懂红黑树，熟练掌握特性是必不可少的一环。

红黑树特性：

①所有节点不是黑色就是红色

②根节点为黑色

③红色节点的左右孩子节点必须为黑色

意思就是不能出现两个红色节点相连的情况。

④每一条路径均含有相同的黑色节点数

从根节点到叶子节点的每一条路径中，黑色节点数量均相同。

⑤叶子节点为黑色

三.红黑树实现原理

实现红黑树，我们需要时刻谨记它的特性，尤其是特性3和4。

（一）.插入节点颜色选择

当插入节点时，如果是插入根节点，那么节点颜色为黑色即可，然后插入完成。

如果是孩子节点，那么先将颜色变为红色，为什么？

如果插入节点颜色是黑色，那么势必打破特性4：所有路径黑色节点数相同。

而如果插入红色，可能会打破特性3：不能有相连的红色节点。

相比于特性4，打破特性3的代价更小：插入黑色势必打破特性4，插入红色则有可能打破特性3。

（二）.插入后，父节点是黑色

当插入孩子节点后，如果父节点是黑色，那么此时没有打破任何一条特性，任务完成。

（三）.插入后，父节点是红色

如果父节点是红色，那么问题就出来了，此时打破了特性3：不能有相连的红色节点。

此时需要分类讨论，而依据就是叔叔节点。

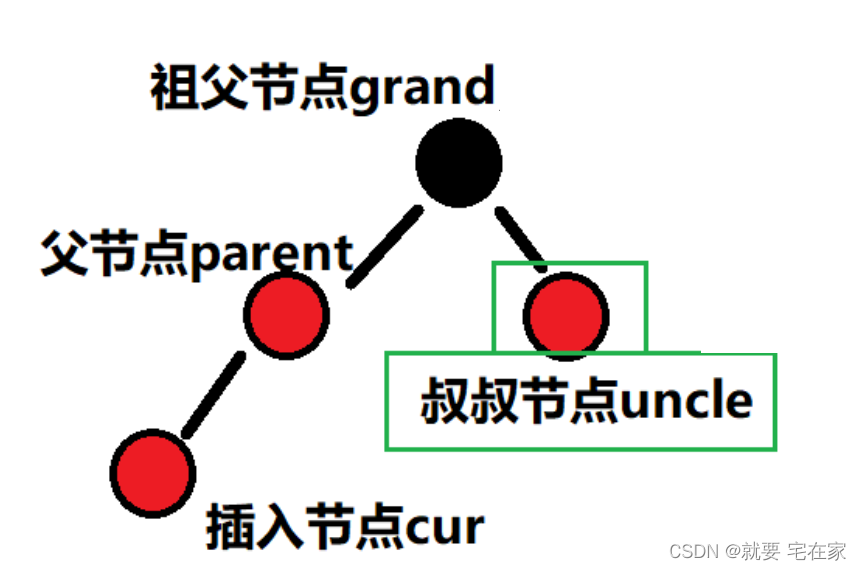
需要考虑的重点是达成每条路径下均含有相同数目的黑色节点（特性4）且没有相连的红色节点（特性3）。

由此，分成（四）、（五）两种情况

（四）.叔叔节点为红色

 将父节点与叔叔节点变为黑色，祖父节点变为红色，然后以祖父节点为“新插入节点”继续向上判断。

①父节点、叔叔节点变黑，祖父节点变红

此时，以祖父为根的树已经满足红黑树的特性要求，因此需要以祖父为出发点继续向上判断，此时祖父的颜色是否依旧符合红黑树，相当于将祖父节点作为“新插入节点”，重新判断。

②以祖父节点为“新插入节点”继续向上判断

（五）.叔叔节点为黑色、没有叔叔节点

需要注意，此时节点并不是真正新插入的节点，因为新插入的节点父节点为红色，说明祖父节点为黑，如果此时叔叔节点为黑色，那么到父节点的这条路径的黑色节点数量就比到叔叔节点的黑色数量少一，说明插入前就已经不是红黑树，这是不成立的。因此，该情况只能出现在祖父节点向上判断时。

这种情况时，单纯的变色已经不能解决问题了，只能靠旋转+变色来解决。

这里不再具体讲解旋转的过程，与AVL树一致，可以参考这篇博客：手把手教你实现AVL树、平衡二叉树

同时，经过旋转+变色后，此时整颗树已经满足红黑树全部特性，即插入完成。 

这时情况可以分成四类，分别对应不同的旋转策略，

前两种均为单旋转，后两种均为双旋转：

①当前节点为父节点左子树，且在根节点左侧

父节点右旋转，父节点变黑，祖父变红。

        步骤一、父节点右旋转

         步骤二、变色

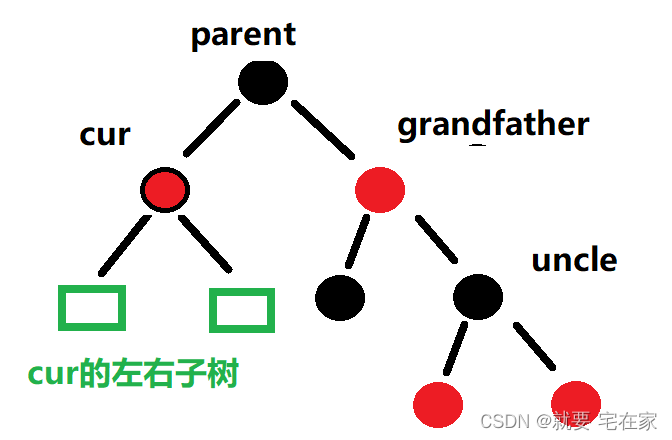
②当前节点为父节点右子树，且在根节点右侧

父节点左旋转，父节点变黑，祖父节点变红

此处类比情况① ，将父节点右旋即可，不再具体演示 

③当前节点为父节点右子树，且在根节点左侧

cur节点左旋转后右旋转，插入节点变黑，祖父节点变红

         步骤一、cur节点左旋转

        步骤二、cur节点右旋转

          步骤三、变色

④当前节点为父节点左子树，且在根节点右侧

cur节点右旋转后左旋转，插入节点变黑，祖父节点变红

此处类比情况③，cur节点右旋后左旋即可，不再具体演示 

四.思维导图

五.实现代码

#pragma once
using namespace std;
#include<iostream>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#define BLACK false//用bool定义红黑颜色
#define RED true
template<class V>
class rb_tree_node//红黑树节点
{
public:
	rb_tree_node(V val)
		:_val(val)
	{}

	bool _col = RED;
	rb_tree_node* right = nullptr;
	rb_tree_node* left = nullptr;
	rb_tree_node* parent = nullptr;
	V _val;
};

template<class V>//红黑树
class rb_tree
{
	typedef rb_tree_node<V> Node;
public:
	void inorder()//中序遍历
	{
		_inorder(_root);//调用函数
	}

	bool Is_RB_Tree()//判断是否为红黑树
	{
		int blackNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK) blackNum++;
			cur = cur->left;
		}
		return _is_rb_tree(_root, 0, blackNum);//调用判断函数
	}

	bool insert(V val);
	
private:
	void _inorder(Node* node)//中序遍历函数
	{
		if (node == nullptr) return;
		_inorder(node->left);
		cout << node->_val << " ";
		_inorder(node->right);
	}
	bool _is_rb_tree(Node* node, int blackNow, int blackNum);//判断函数

	void Rotate_R(Node* cur);
	void Rotate_L(Node* cur);
	Node* _root = nullptr;
};

template<class V>
void rb_tree<V>::Rotate_R(Node* cur)//右旋转
{
	Node* parent = cur->parent, *node_r = cur->right, *grandfather = parent->parent;

	if (node_r)
	{
		node_r->parent = parent;
	}
	parent->left = node_r;

	cur->right = parent;
	cur->parent = grandfather;

	if (grandfather)
	{
		if (grandfather->left == parent) grandfather->left = cur;
		else grandfather->right = cur;
	}
	else _root = cur;
	parent->parent = cur;
}

template<class V>
void rb_tree<V>::Rotate_L(Node* cur)//左旋转
{
	Node* parent = cur->parent, *node_l = cur->left, *grandfather = parent->parent;

	if (node_l)
	{
		node_l->parent = parent;
	}
	parent->right = node_l;

	parent->parent = cur;
	cur->left = parent;

	cur->parent = grandfather;
	if (grandfather)
	{
		if (grandfather->left == parent) grandfather->left = cur;
		else grandfather->right = cur;
	}
	else _root = cur;
}

template<class V>
bool rb_tree<V>::_is_rb_tree(Node* node, int blackNow, int blackNum)
{
	if (node == nullptr) return true;
	if (node->_col == BLACK) blackNow++;
	if (node->left == nullptr && node->right == nullptr)
	{
		if (node->_col == RED && node->parent->_col == RED) return false;
		return blackNow == blackNum;
	}

	if (node != _root && node->_col == RED && node->parent->_col == RED) return false;

	return _is_rb_tree(node->left, blackNow, blackNum) &&
	_is_rb_tree(node->right, blackNow, blackNum);

}


template<class V>
bool rb_tree<V>::insert(V val)
{
	if (_root == nullptr)//插入为根节点
	{
		_root = new Node(val);
		_root->_col = BLACK;
		return true;
	}
	Node* parent = _root->parent, * cur = _root;
	while (cur)
	{
		if (cur->_val == val) return false;//已存在该节点
		if (cur->_val > val)
		{
			parent = cur;
			cur = cur->left;
		}
		else
		{
			parent = cur;
			cur = cur->right;
		}
	}
    //插入节点
	cur = new Node(val);
	cur->parent = parent;
	if (val < parent->_val)
	{
		parent->left = cur;
	}
	else
	{
		parent->right = cur;
	}
    //根据颜色判断是否红黑树
	while (parent && parent->_col == RED)//父节点为红
	{
		Node* grandfather = parent->parent;
		assert(grandfather);//进入循环，说明一定有祖父节点
		assert(grandfather->_col == BLACK);//进入循环，说明祖父节点一定是黑色
		Node* uncle = nullptr;
		if (parent == grandfather->left) uncle = grandfather->right;
		else uncle = grandfather->left;
		if (parent == grandfather->left)//左
		{
			if (uncle && uncle->_col == RED)//变色 + 向上调整
			{
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;
				cur = grandfather;
				parent = cur->parent;
			}
			else if (uncle == nullptr || uncle->_col == BLACK)//叔叔为空，或叔叔为黑
			{
				if (cur == parent->left)//cur为左子树，右单旋
				{
					Rotate_R(parent);
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
				else//cur为右子树，左+右旋+变色
				{
					Rotate_L(cur);
					Rotate_R(cur);
					grandfather->_col = RED;
					cur->_col = BLACK;
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		else//右
		{
			if (uncle && uncle->_col == RED)//变色 + 向上调整
			{
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;
				cur = grandfather;
				parent = cur->parent;
			}
			else if (uncle == nullptr || uncle->_col == BLACK)//叔叔为空，或叔叔为黑
			{
				if (cur == parent->right)//cur为右子树，左单旋
				{
					Rotate_L(parent);
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
				else//cur为左子树，右+左旋+变色
				{
					Rotate_R(cur);
					Rotate_L(cur);
					grandfather->_col = RED;
					cur->_col = BLACK;
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
	}
	_root->_col = BLACK;//根节点一定为黑色
	return true;
}

人类精神必须置于技术之上——Albert Einstein

如有错误，敬请斧正

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/5168.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

web安全渗透之钓鱼网站提权

web安全渗透之钓鱼网站提权

本实验实现1&#xff1a;要生成一个钓鱼网址链接&#xff0c;诱导用户点击&#xff0c;实验过程是让win7去点击这个钓鱼网站链接&#xff0c;则会自动打开一个文件共享服务器的文件夹&#xff0c;在这个文件夹里面会有两个文件&#xff0c;当用户分别点击执行后&#xff0c;则会…
阅读更多...
【数据结构】单链表（不带头结点）基本操作详解——C语言实现

【数据结构】单链表（不带头结点）基本操作详解——C语言实现

&#x1f680; 作者简介&#xff1a;一名在后端领域学习&#xff0c;并渴望能够学有所成的追梦人。 &#x1f40c; 个人主页&#xff1a;蜗牛牛啊 &#x1f525; 系列专栏&#xff1a;&#x1f6f9;初出茅庐C语言、&#x1f6f4;数据结构 &#x1f4d5; 学习格言&#xff1a;博…
阅读更多...
Flink系列文档-(YY08)-Flink核心概念

Flink系列文档-(YY08)-Flink核心概念

1 核心概念 1.1 基础概念 用户通过算子api所开发的代码&#xff0c;会被flink任务提交客户端解析成jobGraph然后&#xff0c;jobGraph提交到集群JobManager&#xff0c;转化成ExecutionGraph&#xff08;并行化后的执行图&#xff09;然后&#xff0c;ExecutionGraph中的各个…
阅读更多...
日志冲突怎么解决?slf4j和log4j的区别?看完这一篇,这些都是小意思啦

日志冲突怎么解决?slf4j和log4j的区别?看完这一篇,这些都是小意思啦

文章目录一.你的烦恼二.前置知识介绍三.说一说让你头大的各种日志依赖1.Slf4j的核心依赖2.log4j的jar包依赖3.slf4j对于log4j的桥接包的依赖4.log4j对于slf4j的逆转包四.再举一些常见小例子使用slf4j作为门面,log4j作为实现需要引入的依赖使用slf4j作为门面,logback作为实现需要…
阅读更多...
[ Linux ] 重定向的再理解，以及文件系统的理解、inode和软硬链接

[ Linux ] 重定向的再理解，以及文件系统的理解、inode和软硬链接

在上篇文章我们了解了Linux中文件描述符和重定向以及缓冲区的理解&#xff0c;本篇文章我们要对了解一下重定向的再理解、文件系统以及引出inode的意义和软硬链接。 目录 0.重定向 0.1标准输出 标准错误 为什么perror2后面跟了一个success 1.inode 1.1 inode理解 一个in…
阅读更多...
一文吃透JavaScript中的DOM知识及用法

一文吃透JavaScript中的DOM知识及用法

文章目录一、前言二、DOM框架三、认识DOM节点四、JS访问DOM1、获取节点2、改变 HTML3、改变 CSS4、检测节点类型5、操作节点间的父子及兄弟关系6、操作节点属性7、创建和操作节点五、快速投票一、前言 DOM&#xff1a;Document Object Model&#xff08;文档对象模型&#xff0…
阅读更多...
指针的进阶应用之双指针、三指针

指针的进阶应用之双指针、三指针

在牛客网和leetcode等网站刷题的过程中&#xff0c;时常会遇到一些使用双指针和三指针解决问题的实例。今天&#xff0c;我来介绍这两种方法&#xff0c;相信你会对指针的应用会提高一个档次。 目录移除元素删除有序数组中的重复项合并两个有序数组在下面的讲解的过程中&#x…
阅读更多...
初步认识系统调用

初步认识系统调用

目录前言一、什么是进程&#xff1f;1、进程与程序的区别&#xff1f;2、什么是进程的控制块二、什么是系统调用&#xff1f;三、认识几个比较简单的系统调用接口1、查看进程2、获取进程的pid/ppid(1).getpid/getppid(2)getpid/getppid的使用3、创建进程的方法总结前言 之前我们…
阅读更多...
Redis系列：Redis持久化机制与Redis事务

Redis系列：Redis持久化机制与Redis事务

Redis 是个基于内存的数据库。那服务一旦宕机&#xff0c;内存中数据必将全部丢失。所以丢失数据的恢复对于 Redis 是十分重要的&#xff0c;我们首先想到是可以从数据库中恢复&#xff0c;但是在由 Redis 宕机时&#xff08;说明相关工作正在运行&#xff09;且数据量很大情况…
阅读更多...
LeetCode刷题记录01

LeetCode刷题记录01

1704判断字符串的两半是否相似序题目我的思路我的代码提交结果其他解简述思路提交结果总结序 我的日常碎碎念&#xff1a;今天下班在看综艺&#xff0c;看到群里班长开了个会议&#xff0c;于是决定开始学习&#xff0c;他说今天的每日一题好简单&#xff0c;让我也去刷一下。嗯…
阅读更多...
数组的定义与使用

数组的定义与使用

文章目录数组的基本概念为什么要使用数组什么是数组数组的创建及初始化数组的创建数组的初始化数组的使用数组中元素的访问遍历数组数组是引用类型基本数据类型与引用类型变量的区别认识null数组的应用场景保存数据作为函数的参数参数传基本数据类型参数传数组类型作为函数的返…
阅读更多...
TFN T6300A 网络综合测试仪 以太网数据 千兆以太网测试仪 OTDR E1 PRI V.35/V.24 光功率计一体机

TFN T6300A 网络综合测试仪 以太网数据 千兆以太网测试仪 OTDR E1 PRI V.35/V.24 光功率计一体机

一款功能强大、便携式、方便使用、价格便宜的高性价比手持式以太网测试仪是企业中网络管理和维护人员的刚需仪器。好的以太网测试仪可以帮助工作人员迅速解决网络不通、网速慢、丢包、延迟等问题。 当今以太网测试仪市场参差不齐&#xff0c;说的功能一个比一个强&#xff0c;…
阅读更多...
你的第一个基于Vivado的FPGA开发流程实践——二选一多路器

你的第一个基于Vivado的FPGA开发流程实践——二选一多路器

你的第一个基于Vivado的FPGA开发流程实践——二选一多路器 1 原理图 2 开发流程 首先我们先打开安装好的Vivado软件 创建一个文件 选择你的开发板 创建一个源文件 现在我们就可以根据原理使用Verilog代码实验这个功能了 module mux2( //端口列表a,b,sel,out);//交代端口类…
阅读更多...
RabbitMQ第二个实操小案例——WorkQueue

RabbitMQ第二个实操小案例——WorkQueue

文章目录RabbitMQ第二个实操小案例——WorkQueueRabbitMQ第二个实操小案例——WorkQueue 讲第二个案例之前&#xff0c;我们先看下前面第一个案例的模型&#xff1a; 可以看到&#xff0c;我们只有一个发布者和一个消费者&#xff0c;通过Queue队列&#xff0c;实现最简单的消…
阅读更多...
02 【nodejs开发环境安装】

02 【nodejs开发环境安装】

02 【nodejs开发环境安装】 1.版本介绍 在命令窗口中输入 node -v 可以查看版本0.x 完全不技术 ES64.x 部分支持 ES6 特性5.x 部分支持ES6特性&#xff08;比4.x多些&#xff09;&#xff0c;属于过渡产品&#xff0c;现在来说应该没有什么理由去用这个了6.x 支持98%的 ES6 特…
阅读更多...
e智团队实验室项目-第三周-经典的卷积神经网络的学习

e智团队实验室项目-第三周-经典的卷积神经网络的学习

e智团队实验室项目-第三周-卷积神经网络的学习 赵雅玲 *, 张钊* , 李锦玉&#xff0c;迟梦瑶&#xff0c;贾小云&#xff0c;赵尉&#xff0c;潘玉&#xff0c;刘立赛&#xff0c;祝大双&#xff0c;李月&#xff0c;曹海艳&#xff0c; (淮北师范大学计算机科学与技术学院&am…
阅读更多...
【树莓派不吃灰】基础篇⑱ 从0到1搭建docker环境，顺便安装一下emqx MQTT Broker、HomeAssistant、portainer

【树莓派不吃灰】基础篇⑱ 从0到1搭建docker环境，顺便安装一下emqx MQTT Broker、HomeAssistant、portainer

目录1. 前言2. 搭建docker环境3. docker简介3.1 docker解决什么问题&#xff1f;3.2 docker VS vm虚拟机3.2.1 vm虚拟机3.2.2 docker3.3 docker如何解决问题&#xff1f;3.4 docker运行架构3.4.1 镜像 : image3.4.2 容器 : container3.4.3 仓库 : repository3.5 国内镜像加速3.…
阅读更多...
python easygui怎么修改默认按钮名字

python easygui怎么修改默认按钮名字

1.执行以下代码找到easygui安装位置 import easyguiprint(easygui.__file__)2.打开上述路径下boxes文件夹下需要修改的组件 如此时想要修改选项栏的默认按钮名字 则打开choice_box.py文件 执行如下图 可以看到有Cancel、SelectALL、ClearALL、OK四个默认按钮&#xff0c;可否…
阅读更多...
Linux下动静态库的制作与使用

Linux下动静态库的制作与使用

学习导航一、关于动静态库的基本认识二、设计库的工程师角度(1)制作静态库(2)制作动态库二、使用库的用户角度(1)使用静态库(2)使用动态库三、理解的角度一、关于动静态库的基本认识 1.静态库 静态库以 .a 作为文件后缀程序在编译链接的时候&#xff0c;将静态库的代码拷贝到…
阅读更多...
[TCP/IP] Linux 搭建服务器局域网

[TCP/IP] Linux 搭建服务器局域网

文章目录[TCP/IP] Linux 搭建服务器局域网1. 使用python内置库http.server2. 使用Http-Server[TCP/IP] Linux 搭建服务器局域网 1. 使用python内置库http.server python3: http.server 命令行启动&#xff1a; # python 3 python -m http.server 8000 # python 2 python -m S…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023