题目来源:码蹄集
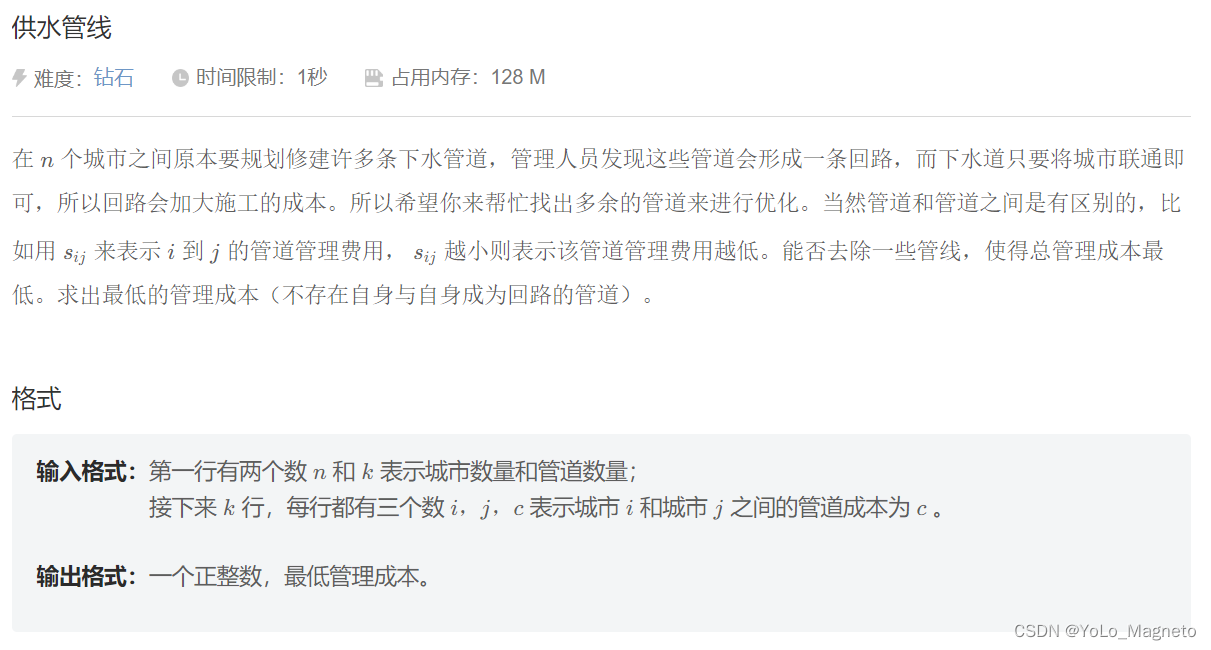
题目描述:
解决思路:
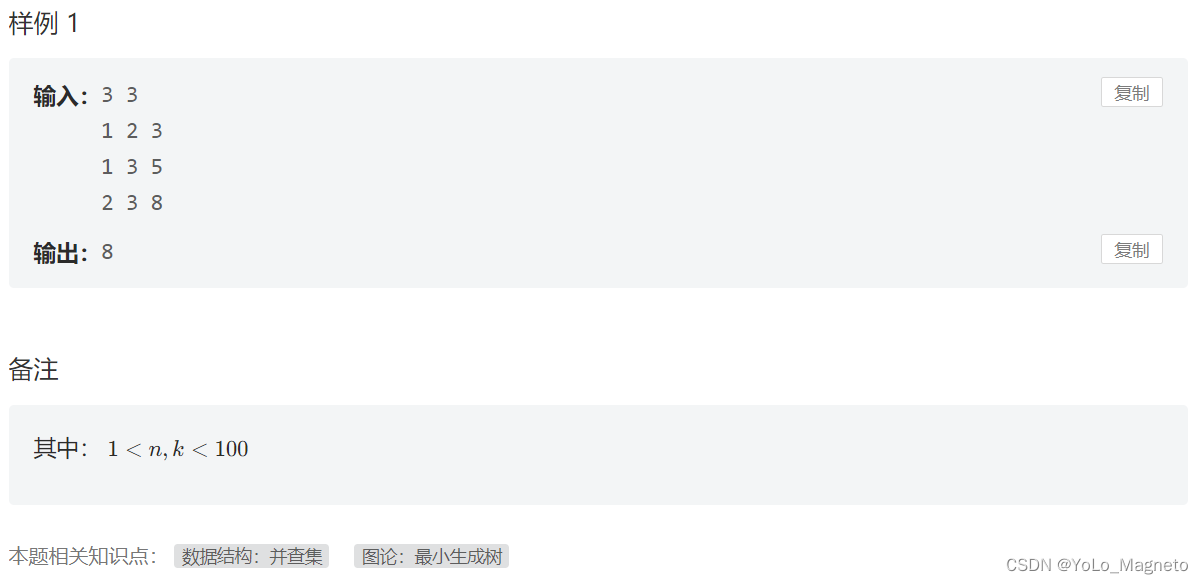
首先,题目要求我们去掉一些管道,使得总的管道管理费用最小。在去掉部分管道的情况下,城市之间不再形成一个回路,即城市之间构成了一棵树。因此,我们需要找到一棵生成树,使得所有管道管理费用之和最小。
接下来,我们需要选择合适的算法来寻找最小生成树。常用的算法有 Kruskal 算法和 Prim 算法,本题使用 Kruskal 算法实现。
Kruskal 算法的实现步骤如下:
-
将所有边按照管道管理费用从小到大排序;
-
依次枚举每条边,如果加入该边不会导致出现环,则将其加入生成树中;
-
当生成树的边数等于 n-1 时,停止枚举。
其中,n 表示城市的数量,生成树的边数为 n-1。
为了判断加入一条边是否会形成环,我们使用并查集维护已经加入生成树中的点的连通关系。具体地,我们让每个节点所在的集合的代表元素相同,这样就能够快速判断两个节点是否属于同一个集合。
最后,根据 Kruskal 算法得到的最小生成树,计算所有边的管理费用之和即可。
Python代码实现:
from typing import List, Tuple
import sys
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, i):
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
def union(self, i, j):
pi, pj = self.find(i), self.find(j)
if pi == pj:
return False
if self.rank[pi] < self.rank[pj]:
pi, pj = pj, pi
self.parent[pj], self.rank[pi] = pi, max(self.rank[pi], self.rank[pj]+1)
return True
def min_cost(n: int, edges: List[Tuple[int, int, int]]) -> int:
uf = UnionFind(n)
edges.sort(key=lambda e: e[2])
mst_cost, num_edges = 0, 0
for u, v, w in edges:
if uf.union(u-1, v-1):
mst_cost += w
num_edges += 1
if num_edges == n - 1:
break
return mst_cost
n, k = map(int, sys.stdin.readline().rstrip().split())
edges = [tuple(map(int, sys.stdin.readline().rstrip().split())) for _ in range(k)]
sys.stdout.write(str(min_cost(n, edges)))
C++代码实现:
#include <bits/stdc++.h>
using namespace std;
struct Edge{
int from, to, cost;
bool operator<(const Edge& e)const{
return cost < e.cost;
}
};
class UnionFind{
vector<int> parent, rank;
public:
UnionFind(int n){
parent.resize(n);
rank.resize(n, 0);
for(int i=0; i<n; ++i)
parent[i] = i;
}
int find(int i){
if(parent[i] != i)
parent[i] = find(parent[i]);
return parent[i];
}
bool union_sets(int i, int j){
int pi = find(i);
int pj = find(j);
if(pi == pj)
return false;
if(rank[pi] < rank[pj])
swap(pi, pj);
parent[pj] = pi;
rank[pi] = max(rank[pi], rank[pj]+1);
return true;
}
};
int main(){
int n, k;
cin >> n >> k;
vector<Edge> edges(k);
for(int i=0; i<k; ++i){
cin >> edges[i].from >> edges[i].to >> edges[i].cost;
edges[i].from--;
edges[i].to--;
}
sort(edges.begin(), edges.end());
UnionFind uf(n);
int mstCost = 0, numEdges = 0;
for(Edge e: edges){
if(uf.union_sets(e.from, e.to)){
mstCost += e.cost;
numEdges++;
if(numEdges == n-1)
break;
}
}
cout << mstCost << endl;
return 0;
}
Java代码实现:
import java.util.*;
class Edge implements Comparable<Edge>{
int from, to, cost;
public Edge(int from, int to, int cost){
this.from = from;
this.to = to;
this.cost = cost;
}
@Override
public int compareTo(Edge e){
return this.cost - e.cost;
}
}
class UnionFind{
int[] parent;
int[] rank;
public UnionFind(int n){
parent = new int[n];
rank = new int[n];
for(int i=0; i<n; ++i)
parent[i] = i;
}
public int find(int i){
if(parent[i] != i)
parent[i] = find(parent[i]);
return parent[i];
}
public boolean union(int i, int j){
int pi = find(i);
int pj = find(j);
if(pi == pj)
return false;
if(rank[pi] < rank[pj]){
int temp = pi;
pi = pj;
pj = temp;
}
parent[pj] = pi;
rank[pi] = Math.max(rank[pi], rank[pj]+1);
return true;
}
}
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
UnionFind uf = new UnionFind(n);
List<Edge> edges = new ArrayList<>();
for(int i=0; i<k; ++i){
int u = scanner.nextInt()-1;
int v = scanner.nextInt()-1;
int w = scanner.nextInt();
edges.add(new Edge(u, v, w));
}
Collections.sort(edges);
int mstCost = 0, numEdges = 0;
for(Edge e: edges){
if(uf.union(e.from, e.to)){
mstCost += e.cost;
numEdges++;
if(numEdges == n-1)
break;
}
}
System.out.println(mstCost);
}
}
代码提交测试结果:
附B站老师讲解链接,可供参考:https://www.bilibili.com/video/BV1cs4y137za/?t=551.4