2.1 二元分类

前言

第二周的主题是学习神经网络的基础知识。

实现神经网络需要用到一些重要的技术和技巧，比如怎样处理包含大量样本的训练集。

在神经网络的计算中，还会有前向暂停、前向传播、反向暂停和反向传播等步骤，本周会对它们进行详细的介绍。

本周课程中会使用逻辑回归这个算法来帮助大家理解这些概念。

正题

逻辑回归算法一般用于二元分类问题，下面这个问题就是一个典型的二元分类问题。

题目

输入一张图片，若识别这张图片里有猫，则输出标签1作为结果，否则输出标签0作为结果。

分析

图片在计算机中的表示方法

计算机中有红、绿、蓝三种色块，三种色块按照不同的深浅度叠加就是一个像素，一张图片就由许多像素组成。

我们用三个矩阵来表示三种色块，矩阵中的元素值就是像素的强度值，这里用三个5x4的矩阵来表示一张图片：

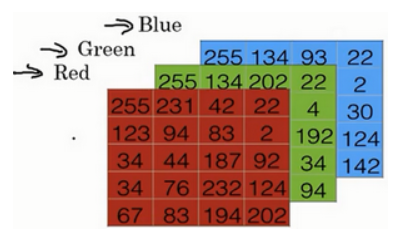
为了将图片输入到计算机中，我们需要将像素值放到一个特征向量里，这是一个列向量，从上到下地存放像素值，先存放第一个矩阵的第一行，再存放第一个矩阵的第二行，......，最后存放第三个矩阵的最后一行。

这个特征向量的行数就是所有像素的数量（注意不是像素值的和），我们通常用x来表示特征向量，用n来表示特征向量的维度（即行数）。

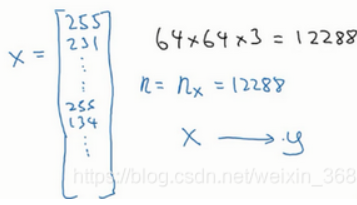
所以，在二元分类问题中，我们的目标就是构建一个分类器，它以图片的特征向量作为输入，然后输出结果y（1或0），也就是预测图片中是否有猫。

符号定义

接下来我们说明一些在下面的课程中会用到的符号。

• x

表示一个输入的n维的数据（向量）。

• y

表示输出结果，取值范围为{1，0}。

• (x(i),y(i))

表示第i组数据，(i)为上标，可以是训练数据，也可以是测试数据，这里默认为训练数据。

• X=[x(1),x(2),⋯,x(m)]

大写的X表示所有训练数据集的输入值，放在一个n行m列的矩阵中，其中m表示样本个数。

有时候会出现训练样本按行堆叠起来的矩阵，这时候要将其转置，这样处理起来才更简单。

• Y=[y(1),y(2),⋯,y(m)]

大写的Y表示所有训练数据集的输出值，放在一个1行m列的矩阵中，也就是一个行向量。

在python中，输出X的命令是：X.shape；输出Y的命令是：Y.shape。

2.2 逻辑回归算法

前一篇文章提到，给定一个特征向量x作为输入，x对应着一张图片，我们需要一个算法来预测图片里是否有猫，这里注意，我们的输出是预测，所以只是对实际值y的预测，用y^来表示。

y^是预测值，也就是y=1的概率，其取值范围为[0,1]。

此时，再给出两个参数，n维向量w是逻辑回归的参数，b是偏差，利用公式y^=w(T)x+b可以粗略地得出一个预测值，但是不能保证这个值处于0和1之间。

上面的这个公式其实就是线性回归的公式，但仅仅靠这个公式是无法解决二分类问题的，需要再使用Sigmoid函数。这个函数能将线性回归公式的结果转化为介于0和1之间的概率。