---

一、介绍

1、什么是堆

堆是一种叫做完全二叉树的数据结构，可以分为大项堆，小项堆，而堆排序就是基于这种结构而产生的一种程序算法。

2、大项堆（排序前）

大项堆:每个节点的值都大于或者等于他的左右孩子节点的值

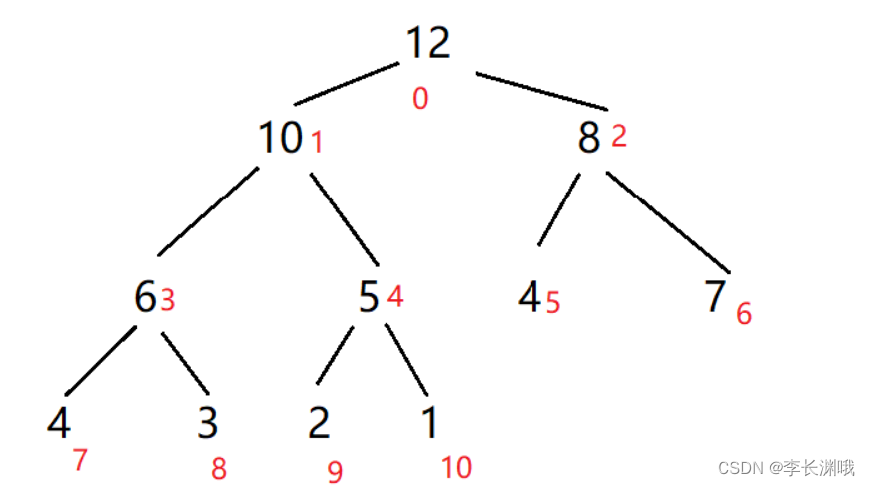
3、小项堆（排序前）

小项堆:每个结点的值都小于或等于其左孩子和右孩子结点的值

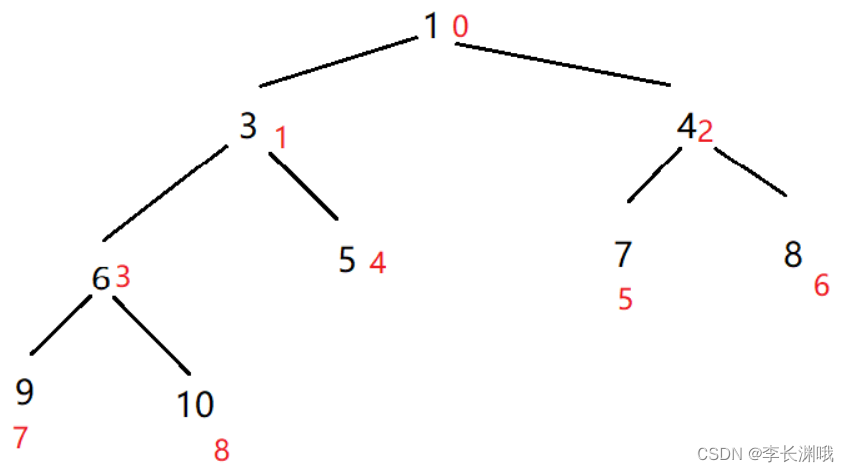
4、排序思想

父–>子:i—>左孩子:2i+1, 右孩子:2i+2;
子–>父:i—>(i-1)/2; (i为下标元素)

1. 首先将待排序的数组构造成一个大项堆，此时，整个数组的最大值就是堆结构的顶端
2. 将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1
3. 将剩余的n-1个数再构造成大项堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

注意:升序用大项堆，降序就用小项堆(默认为升序)

二、大项堆排序案例

1、流程

1. 从最后一棵子树开始,从后往前调整
2. 每次调整,从上往下调整
3. 调整为大根堆

2、讲解

首先我们给定一个无序的序列，将其看做一个堆结构，一个没有规则的二叉树，将序列里的值按照从上往下，从左到右依次填充到二叉树中。

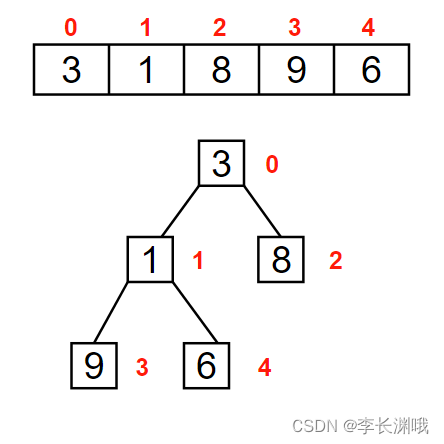
在这里1小于最大值子节点9，则交换1和9的位置

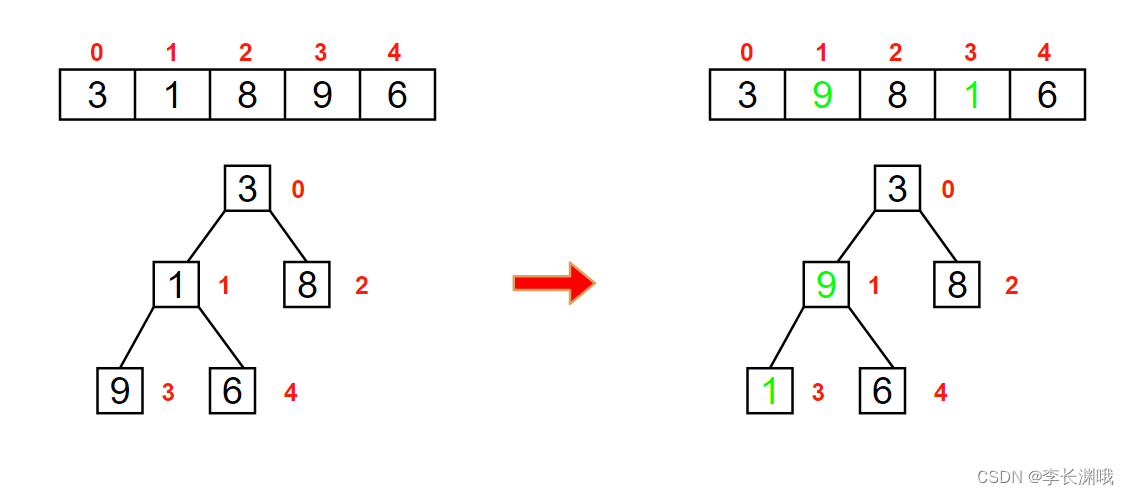
找到下一个非叶子节点3，用它和它的左右子节点进行比较，3小于最大值子节点9，交换3和9位置

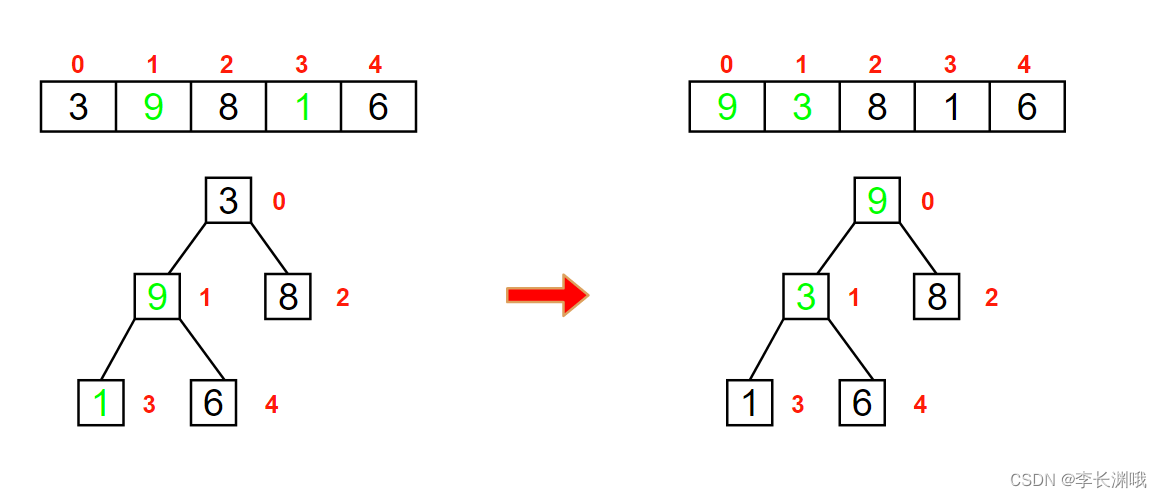
此时发现3小于6这个最大值子节点，我们需要进行调整，因此交换6和3的位置

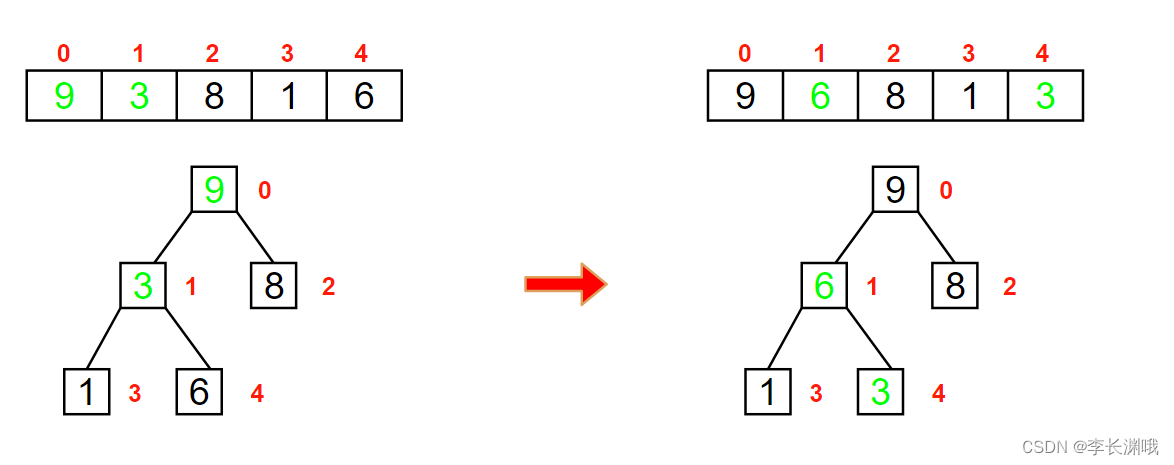
此时我们就构造出来一个大根堆,下来进行排序
首先将顶点元素9与末尾元素3交换位置，此时末尾数字为最大值。排除已经确定的最大元素，将剩下元素重新构建大根堆
一次交换重构如图:

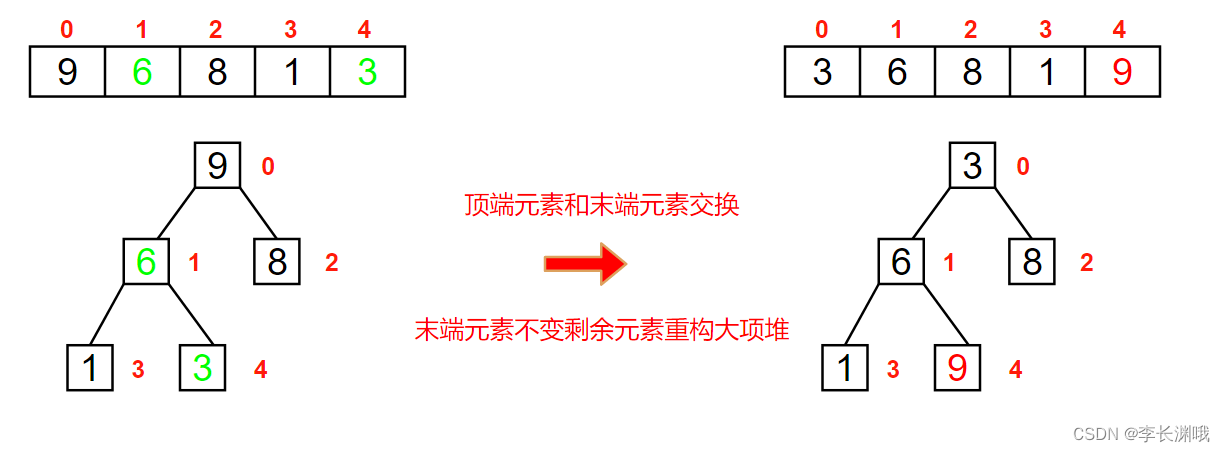
最终排序结果:

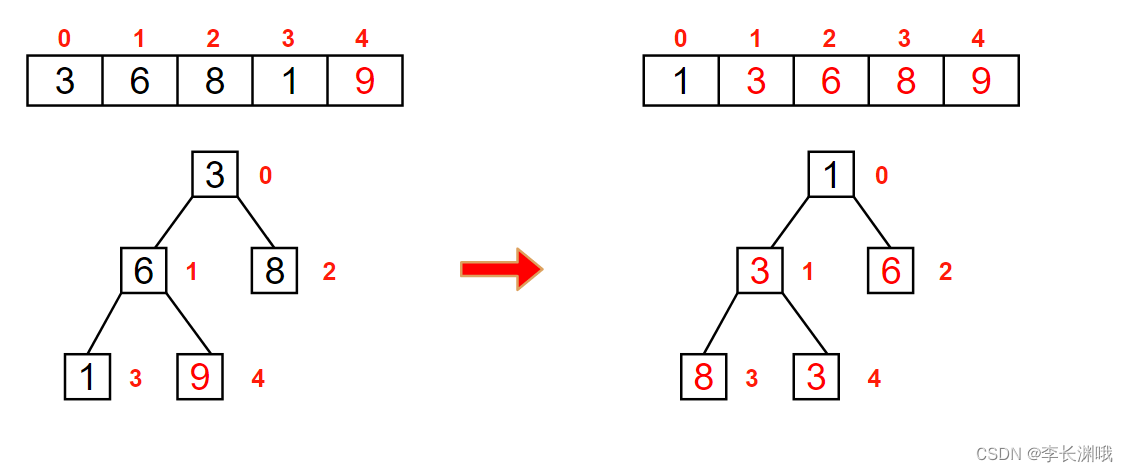
三、总结

由此，我们可以归纳出堆排序算法的步骤：

1. 把无序数组构建成二叉堆。
2. 循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

堆排序是不稳定的排序，空间复杂度为O(1),平均的时间复杂度为O(nlogn),最坏情况下也稳定在O(nlogn)