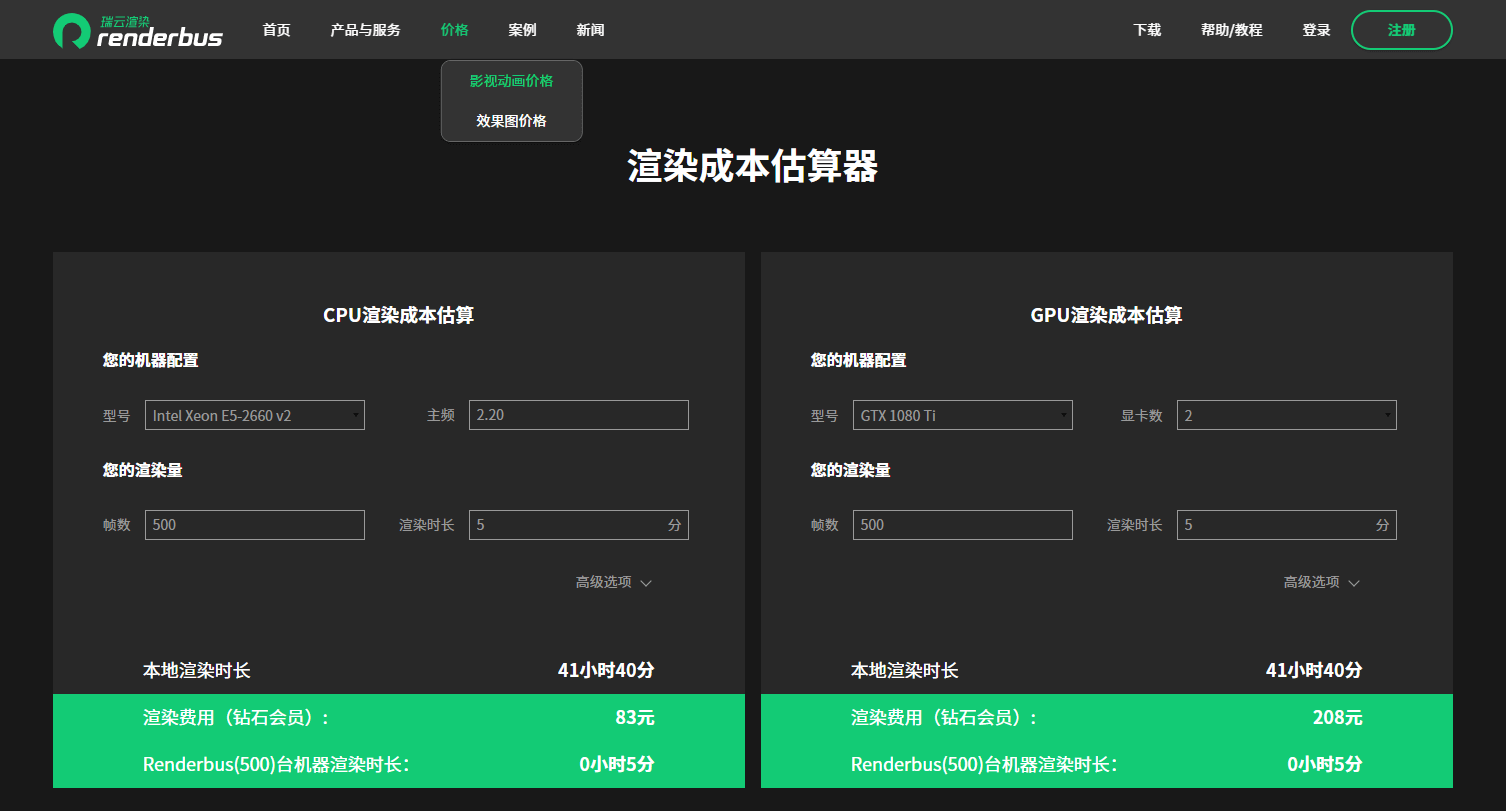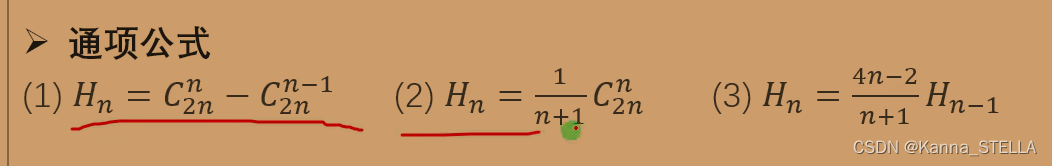
前提条件：

有两种操作，一种操作的次数不能超过另外一个，或者是不能有交集这些操作的合法方案数，通常是卡特兰数

情景：

1）n个0和n个1构成的字串，所有的前缀子串1的个数不超过0的个数，求这样的字串个数

向上的操作不超过向右的操作

2）包含n组括号的合法式子：

与情景1的练习：左括号对于0，右括号对应1

3） 一个栈的进栈序列为1,2,3,…,m,有多少个不同的出栈序列 ?

4）n个节点可以构造多少个不同的二叉树。

5）在圆上选择2n个点，将这些点成对连接起来所得到的n条弦不相交的方法数

6）通过连结顶点而将n+2边的凸多边形分成n个三角形的方案数

形式：

1 1 2 5 14 42 132 429 1430……

推导：

一式：

曲线救国。
1.求总路径数
2.求非法
3.相减得到合法
step1总路径就是2n次操作里选n次向右的方案数
$$C_{2n}^n$$

step2对于y = x + 1，
所有的非法路径都必然与其有一个交点。
从第一个交点开始路径对于y = x + 1对称
路径会对称到终点为（n-1，n+1）的点。
所以非法路径数就是$$C_{2n}^{n-1}$$
step3二者相减：
$$到达点(n,n)的合法路径数就是H_n=C_{2n}^n-C_{2n}^{n-1}$$

二式：

1.明确需要配凑的式子：$$\frac{1}{n+1}\frac{2n!}{n!n!}，即C_{2n}^n$$
2.一式写成阶乘形式
3.提公因式$$提这个公因式\frac{2n!}{n!(n-1)!}，得到\frac{2n!}{n!(n-1)!}\ast (\frac{1}{n}-\frac{1}{n+1})$$
4.通分括号内的式子，再把提取出的公因式与之相乘。配凑出$$\frac{1}{n+1}\frac{2n!}{n!n!}，即\frac{1}{n+1}{C}_{2n}^n,over$$

三式

1.明确需要配凑的式子：$$Catala{n}_{n-1}$$
2.拆解$$Catala{n}_n$$
3.配凑出需要的式子，
4.剩下的式子约分。
step1明确$$Catala{n}_{n-1}=\frac{1}{n}{C}_{2n-2}^{n-1}=\frac{1}{n}\frac{(2n-2)!}{(n-1)!(n-1)!}$$
step2拆解$$Catala{n}_n=\frac{1}{n+1}{C}_{2n}^n=\frac{1}{n+1}\frac{2n!}{n!n!}$$
step3配凑$$得到\frac{1}{n+1}\frac{(2n-1)(2n)}{n}\ast \frac{1}{n}\frac{(2n-2)!}{(n-1)!(n-1)!}$$

step4化简$$\frac{4n-2}{n+1}\ast \frac{1}{n}{C}_{2n-2}^{n-1}=Catala{n}_{n-1}$$