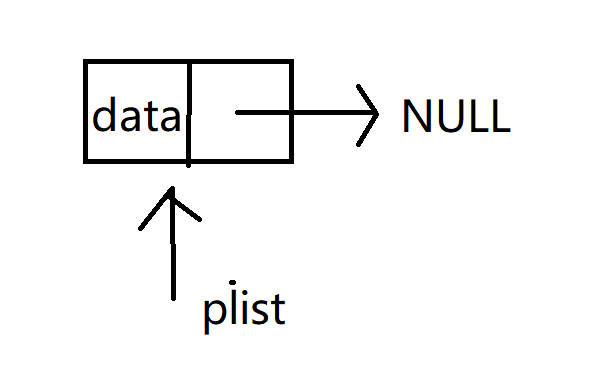
伸展树的概念

伸展树（Splay Tree）是仅依靠局部性原理和局部平衡分析，从而实现高效的自适应平衡树结构。是一种二叉查找树，其核心思想是将最近访问的节点旋转到根节点。每次进行访问、插入、删除等操作时，都会选择与之操作的节点作为根节点进行旋转。通过不断进行旋转操作，会引起每次访问节点和其父节点之间的关系发生变化，从而使得经常被访问的节点移动到树顶部，而不常被访问的节点则移动到树的底部。

伸展树中最重要的操作是旋转（Splay），旋转操作可以分为一次旋转和双旋转两种情况。一次旋转是将一个节点沿其父节点的左右儿子其中一个进行旋转，双旋转则是在一次旋转的基础上再进行一次旋转。

伸展树的平衡性是通过特殊的旋转来实现的。特别地，伸展树在每次插入或者删除一个节点后，都将它旋转到根节点，从而维护树的平衡性。

伸展树的实现

在学习伸展树之前，我们需要了解AVL树，明白了AVL树中的旋转，那么伸展树理解起来就不是什么难事了。想了解AVL树可以参考下面这篇博客。

AVL树详解_小白麋鹿的博客-CSDN博客https://yt030917.blog.csdn.net/article/details/130176502其实说白了，伸展树就是每次对一个节点操作之后，把它移动到根的位置。我们可以先通过递归找到这个节点，在递归回去的过程中对其旋转。具体的实现见代码。

要注意，伸展树是一种二叉查找树，但并不是平衡二叉树，这里不要混淆了。

伸展树视频演示

也可以自己尝试：

Splay Tree Visualzation (usfca.edu)https://www.cs.usfca.edu/~galles/visualization/SplayTree.html

代码示例

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

typedef char ElementType;
typedef struct SplayTreeNode
{
	ElementType Data; //暂定节点内容只有单个字符
	int Height;
	struct SplayTreeNode* Left;
	struct SplayTreeNode* Right;
}SplayTree;

int Height(SplayTree* Node) //规定叶节点的高度为1
{
	if (Node == NULL)
		return 0;
	return Node->Height;
}
//单左旋，指的是左边节点进行旋转，并不是指的旋转到左边（这与大多数教程是不同的，但是无伤大雅）
SplayTree* SingleLeftRotate(SplayTree* k2) 
{
	//旋转节点
	SplayTree* k1 = k2->Left;
	k2->Left = k1->Right;
	k1->Right = k2;
	//更新高度
	k2->Height = max(Height(k2->Left), Height(k2->Right)) + 1;
	k1->Height = max(Height(k1->Left), Height(k1->Right)) + 1;
	//返回
	return k1;
}
//单右旋，指的是右边节点进行旋转，并不是指的旋转到右边（这与大多数教程是不同的，但是无伤大雅）
SplayTree* SingleRightRotate(SplayTree* k2) 
{
	//旋转节点
	SplayTree* k1 = k2->Right;
	k2->Right = k1->Left;
	k1->Left = k2;
	//更新高度
	k2->Height = max(Height(k2->Left), Height(k2->Right)) + 1;
	k1->Height = max(Height(k1->Left), Height(k1->Right)) + 1;
	//返回
	return k1;
}
SplayTree* InsertElement(SplayTree** root, ElementType data)
{
	//走到空节点（即插入位置），执行插入操作 
	if ((*root) == NULL)
	{
		(*root) = (SplayTree*)calloc(1, sizeof(SplayTree)); 
		(*root)->Data = data; 
	}
	//data比节点的值小，向左侧插入
	else if(data < (*root)->Data)
	{
		(*root)->Left = InsertElement(&(*root)->Left, data);
	}
	//data比节点的值大，向右侧插入
	else if (data > (*root)->Data)
	{
		(*root)->Right = InsertElement(&(*root)->Right, data);
	}
	//data与节点的值相同，暂定什么都不做   
	else {  /*暂定如果插入的元素内容相同的话，那么什么都不会做*/ }
	//更新高度
	(*root)->Height = max(Height((*root)->Left), Height((*root)->Right)) + 1;
	//返回
	return *root;
}
//这里是将查找和伸展操作放在同一个函数的，所以就会出现即使data不在树中也会执行伸展操作，
//一般是将理论上离data最近的节点移到根位置。要想实现只有当data出现在树中才伸展，
//可以考虑用一个额外的函数判断data是否存在，进而决定是否需要伸展
bool FindElement(SplayTree** root, ElementType data) //在以*root为根的树中查找data元素。同时对树进行伸展
{   
	//没找到，返回NULL    
	if ((*root) == NULL)
	{
		puts("404 - Not Found!");
		return false;
	}
	//data小，向左走
	else if (data < (*root)->Data)
	{	
		if(FindElement(&(*root)->Left, data) != 0)
			(*root) = SingleLeftRotate((*root));
	}
	//data大，向右走
	else if (data > (*root)->Data)
	{
		if (FindElement(&(*root)->Right, data) != 0)
			(*root) = SingleRightRotate((*root));
	}
	//返回
	return true;
	
}
int main()
{
	SplayTree* root = NULL;
	InsertElement(&root, 'h');
	InsertElement(&root, 'd');
	InsertElement(&root, 'e');
	InsertElement(&root, 'b');
	InsertElement(&root, 'c');
	InsertElement(&root, 'j');
	InsertElement(&root, 'p');
	InsertElement(&root, 'x');
	InsertElement(&root, 't');
	InsertElement(&root, 'f');
	puts("************** insert over ****************");
	FindElement(&root, 'e');
	//FindElement(&root, 'x');
	puts("**************  find over  ****************");
	return 0;
}