Acceptance-Rejection Sampling

文章目录

• Acceptance-Rejection Sampling
• • @[toc]
  • • 1 接受拒绝采样
    • 2 Acceptance-Rejection 采样实现

1 接受拒绝采样

给定随机变量$X$服从pdf为$f(x)$的分布，例如$f(x)$为正态概率密度函数，我们可以通过相关统计软件自动生成满足特定分布的样本数据。假如$f(x)$不服从正态分布，而是服从如下这种比较复杂的分布该如何进行观测采样呢？
$$X\sim f(x)=\frac{sin(x^2)+cos(x)+2}{{\int }_a^{b}sin(x^2)+cos(x)+2dx},x\in [a,b]$$
此外，我们还要基于所采样的样本计算相关统计量，例如一阶矩、二阶矩等，这需要计算更为复杂的函数积分，又该如何计算？针对上述一系列问题，数学中衍生出接受拒绝采样(Acceptance-Rejection Sampling)，该方法采用了Monte Carlo思想。

已知存在如下概率密度函数$f(x)$，随机变量$X\sim f(x)$，$x\in [a,b]$

为了获得服从$f(x)$的随机样本，引入一个均匀分布，随机变量$Y\sim U(a,b)$，对应的概率密度函数为$g(y)=\frac{1}{b-a}$

将概率密度曲线$g(y)$向上平移，直至存在最小的常数$c$，使得对于任意来源于$g(x)$的样本值$x$都有
$$cg(x)=\frac{c}{b-a}\ge f(x)$$

现在假设已经获得来源于$g(x)$的一个样本值$x^{\ast }$,构建如下比例
$$z=\frac{f(x^{\ast })}{cg(x^{\ast })}\in [0,1]$$

若$z$值越大，表明目标分布$f(x^{\ast })$与均匀分布$g(x)$越靠近，此时选择或承认$x^{\ast }$(来源于均匀分布$g(x)$）这个样本值作为目标分布$f(x)$的一个采样的概率就越大。如果选择承认$x^{\ast }$是$f(x)$的一个样本采集，那就接受$x^{\ast }$。

那么，给定一个$z$值，如何判断对应的$x^{\ast }$是否接受呢？再引入随机变量$u\sim U(0,1)$，并从该均匀分布获得一个样本值$u\in [0,1]$，如果$z$值较大，那么$z>u$的概率也较大。显然，如果$x^{\ast }$越接近0（上图中），那么选择接受$x^{\ast }$附近的观测频率就越高。通过对$g(x)$大量的样本观测采集，将$z$值与$u$值进行比较，就可得到目标分布函数的样本近似观测。

上述$g(x)$又称为建议分布(proposal distribution)，顾名思义就是从$g(x)$中获得一个样本观测$x^{\ast }$，建议$f(x)$的样本是否采用$x^{\ast }$,如果建议，则接受，反之拒绝。上文说的建议分布$g(x)$服从均匀分布，事实上，可以选择其他分布，$g(x)$满足接近$f(x)$且覆盖$f(x)$区域，Acceptance-Rejection Sampling效率越高。

---

强行总结下，实现Acceptance-Rejection Sampling步骤如下：

1)目的：已知较为复杂的目标分布$f(x)$，需要从$f(x)$进行样本采集；

2)构建建议分布G,选择密度函数为均匀分布的$g(x)=\frac{1}{b-a}$；

3)寻找最小常数$c$，使得$cg(x)=\frac{c}{b-a}\ge f(x)$;

4)再获得一个随机变量$u\sim U(0,1)$;在计算机模拟中就是获得一个在(0,1)上的随机数；

5)从$g(x)$中获得$x^{\ast }$，并计算$z=\frac{f(x^{\ast })}{cg(x^{\ast })}$；

6)if $z>u$则接受$x^{\ast }$;else 拒绝

7)重复步骤4-6，直至得到预期样本量$n$

---

2 Acceptance-Rejection 采样实现

给定如下概率密度函数，对其进行样本采样
$$f(x)=\frac{sin(x^2)+cos(x)+2}{{\int }_a^{b}sin(x^2)+cos(x)+2dx},x\in [a,b]$$
假设$a=-10,b=10$。对该密度函数可视化，由于分母是常数，只需看分子的图像即可。

g = function(x) sin(x^2)+cos(x)+2
par(mfrow = c(1,1))
curve(g,n=1000,from = -10,to = 10)
# 这里的int即为最小常数c
int = integrate(g,-10,10)$value

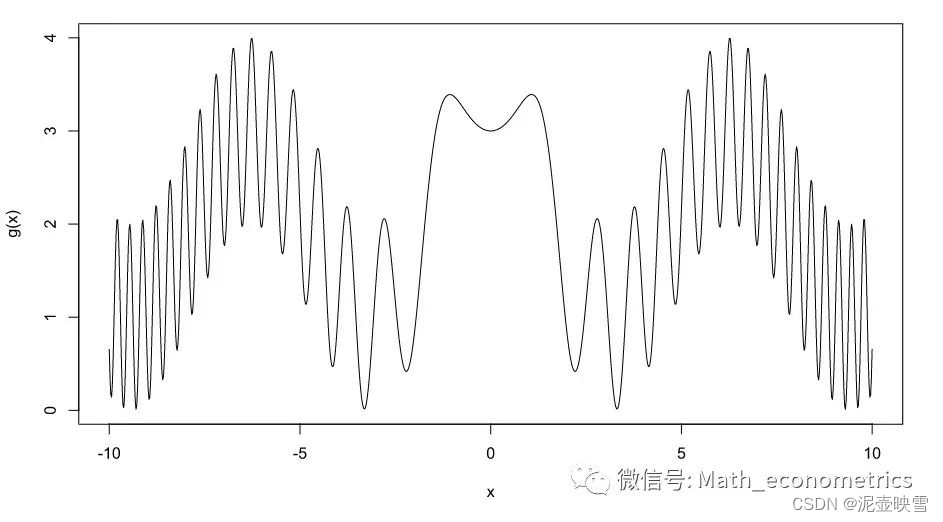
该密度函数是对称函数，具有多峰性。下面分别采集100，1000，10000和20000样本量

n = c(100,1000,10000,20000)   
par(mfrow = c(2,2))
for(i in 1:4){
  k = 0
  x = numeric() 
  while(k < n[i]){
    # 均匀分布
    u = runif(1) 
    # 从建议分布获得x*
    y = runif(1,-10,10) 
    # 判断
    if((sin(y^2)+cos(y)+2)/int > u){  
      cat('Accept',k,'\n')
      k = k + 1  
      x[k] = y  
    }else{
      cat('Reject',k,'\n')
    }
    cat('=====😁=====',k,'=====😁=====\n')
  }
  
  # 绘制直方图
  hist(x,prob=T,col = 'red',breaks = seq(-10,10,0.1),
       main = paste('n=',n[i]))  
  X = seq(-10,10,0.01)
  # 真实密度曲线
  Y = (sin(X^2)+cos(X)+2)/int  
  lines(X,Y,lwd = 3)
}

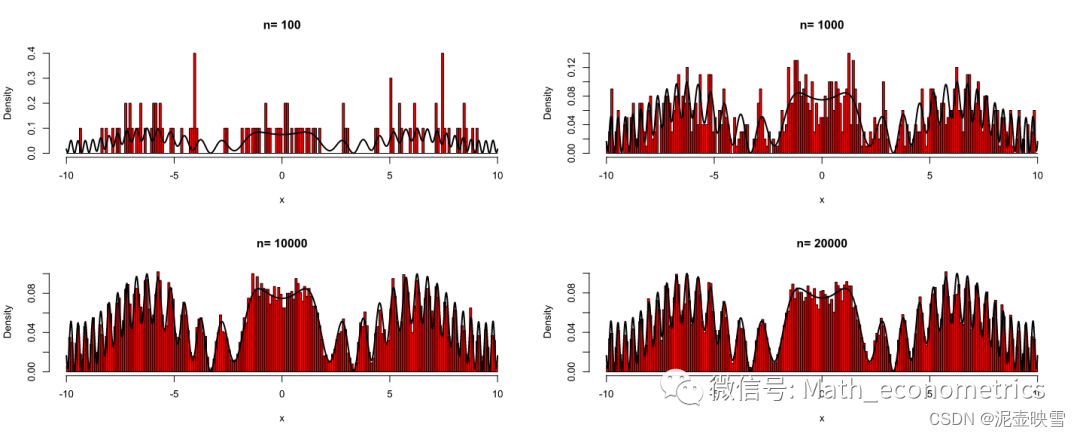
上图可以发现随着样本采集次数越多，对目标分布的近似采集效果越好。

---