引入——泛型编程

如果我们需要实现不同数据类型的Swap函数，需要手写很多内容类似的结构。如下。

void Swap(int& x, int& y)
{
	int tmp = x;
	x = y;
	y = tmp;
}

void Swap(double& x, double& y)
{
	double tmp = x;
	x = y;
	y = tmp;
}

//……

这样既在书写代码的过程中可能出现错误，又不好维护，效率不高。
由此，我们选择将这个任务交给编译器完成。我们给编译器一个“模具”，让编译器根据“摸具”创建出具体的“实例”。

在这里插入图片描述

泛型编程：编写与类型无关的通用代码，是代码复用的一种手段。模板是泛型编程的基础。

在这里插入图片描述

一、函数模板

（以上面 Swap 函数为例）

template<typename T>
void Swap(T& x, T& y)
{
	T tmp = x;
	x = y;
	y = tmp;
}

注：typename 是用来定义模板参数 关键字，也可以使用 class(不能使用 struct )

1.函数模板格式

template<typename T1, typename T2,......,typename Tn>
返回值类型 函数名(参数列表)
{   }

2.函数模板原理

template<class T>
void Swap(T& x, T& y)
{
	T tmp = x;
	x = y;
	y = tmp;
}

int main()
{
	int a = 13, b = 7;
	Swap(a, b);
	cout << "a=" << a << " " << "b=" << b << endl;

	double c = 1.13, d = 1.7;
	Swap(c, d);
	cout << "c=" << c << " " << "d=" << d << endl;

	return 0;
}

在这里插入图片描述

在编译器编译阶段，对于模板函数的使用，编译器需要根据传入的实参类型来推演生成对应类型的函数以供调用。比如：当用double类型使用函数模板时，编译器通过对实参类型的推演，将T确定为double类型，然后产生一份专门处理double类型的代码，对于字符类型也是如此。

3.模板的实例化

隐式：让 编译器 根据实参推演模板参数的实际类型

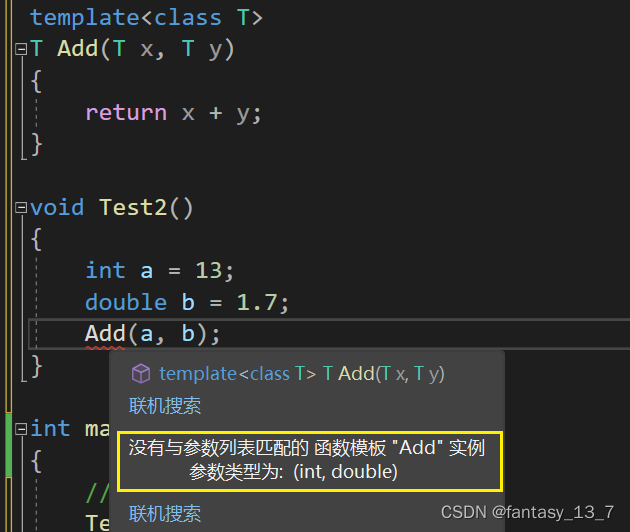
如上，编译器无法根据实参推演模板参数的实际类型。
两种解决办法：
①强制类型转化：Add(a, (int)b);
②显式实例化：Add<int>(a, b);

显式：在函数名后的<>中指定模板参数的实际类型

template<class T>
T Add(T x, T y)
{
	return x + y;
}

void Test2()
{
	int a = 13;
	double b = 1.7;
	Add<int>(a, b);
}

4.模板参数的匹配原则

一个非模板函数可以和一个同名的函数模板同时存在，而且该函数模板还可以被实例化为这个非模板函
数
对于非模板函数和同名函数模板，如果其他条件都相同，在调动时会优先调用非模板函数而不会从该模板产生出一个实例。如果模板可以产生一个具有更好匹配的函数，那么将选择模板
（例如，如上图，对于 int 数据类型，调用 Add 函数时会优先调用 专门处理 int 的 Add 函数 ）
模板函数不允许自动类型转换，但普通函数可以进行自动类型转换

二、类模板

0.引入

template<class T>
class Stack
{
private:
	T* _arry;
	int _top;
	int _capacity;
};

int main()
{
	Stack<int> st1;
	Stack<double> st2;

	return 0;
}

在这里插入图片描述

1.类模板的定义格式

template<class T1, class T2, ..., class Tn>
class 类模板名
{
 // 类内成员定义
};

2.类模板的实例化

// 动态顺序表
// 注意：Vector不是具体的类，是编译器根据被实例化的类型生成具体类的模具
template<class T>
class Vector
{
public:
	Vector(size_t capacity = 10)
		: _pData(new T[capacity])
		, _size(0)
		, _capacity(capacity)
	{}

	// 使用析构函数演示：在类中声明，在类外定义。
	~Vector();

private:
	T* _pData;
	size_t _size;
	size_t _capacity;
};
// 注意：类模板中函数放在类外进行定义时，需要加模板参数列表
template <class T>
Vector<T>::~Vector()
{
	if (_pData)
		delete[] _pData;
	_size = _capacity = 0;
}

int main()
{
	Vector<int> v;
	return 0;
}