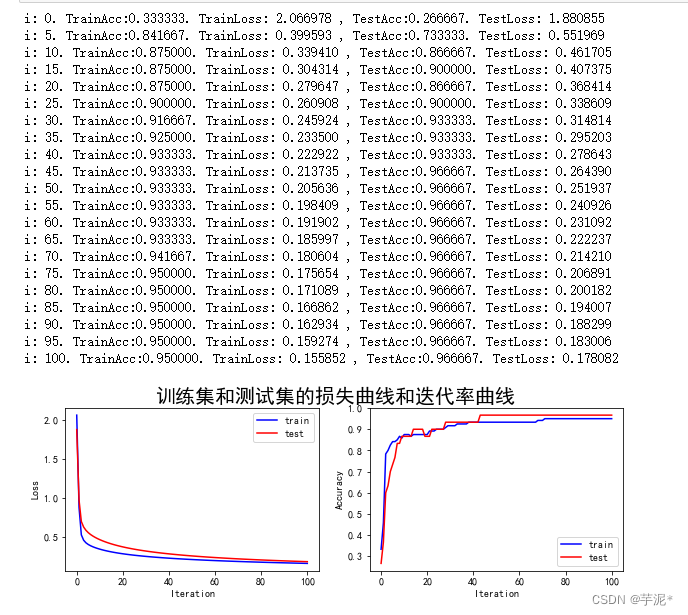
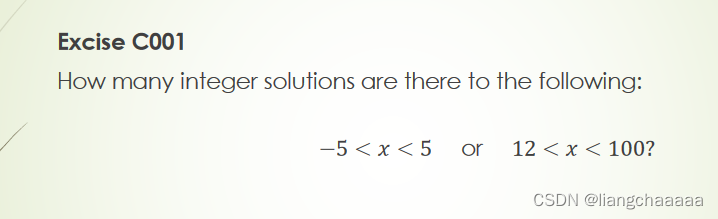组合数学第一讲

news2024/11/29 13:44:54

加法原则

4+3+2 = 9

87+9 = 96

乘法原则

3 * 2 = 6

800 = 2^5+5^2

因子可写成2^x+5^y，其中x = 0,1,2,3,4,5 y = 0,1,2

6*3 = 18

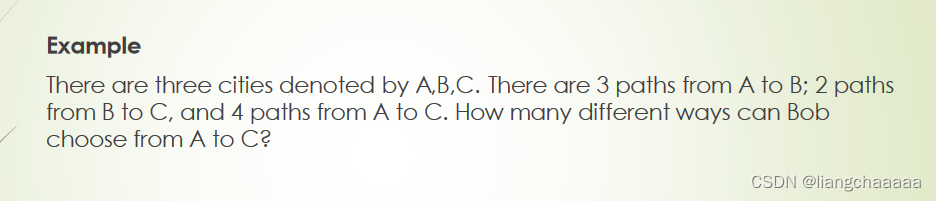
4 + 3 * 2 = 10

数学归纳法

关键：假设n是正确的，证明n+1也是正确的

Horse paradox（马悖论）

用PMI证明出了马悖论……

待证命题：所有的马都是同一个颜色

使用数学归纳法进行证明，只需要两步。

(1) 我们要证明，当 n = 1 的时候，命题是正确的；

(2) 我们假设当 n = k 的时候，命题是正确的；然后证明出，当 n = k + 1 的时候，命题也是正确的。

n = 1时，只有一匹马，显然只有一种颜色

假设n = k时，n匹马都是相同的颜色，现在可否证明n = k+1时，该命题依旧成立

First, exclude one horse and look only at the other n horses;all these are the same color since n horses always are the same color.
Likewise, exclude some other horse and look only at the other n horses. These must also be of the same color.
So, If n horses have the same color, then n+1 horses will also have the same
color.

从K+1匹马中选出一匹马，则剩下的K匹马都是一个颜色（假设条件），接着依次从K+1匹马中选取一匹马，都能得到剩余的K匹马是同种颜色，由此，如果K匹马同色，则K+1匹马同色。

比如：

1.去掉2号的马，剩下的马(1,3,4,...,k+1)同色；所以1和3,4,5,6,...,k+1同色

2.去掉3号的马，剩下的马(1,2，4,..,k+1)同色。所以1和2同色

所以1~k+1同色

证明的错误有个形象的比喻：把数学归纳法比喻成多米诺骨牌。以上的递推步的证明就好比多米诺骨牌的第一块和第二块之间间隔太大, 推倒了第一块, 但它不会推倒第二块. 即使我们知道第二块倒下会推倒第三块, 第三块倒下会推倒第四块等等, 但第三, 第四等等后面的骨牌并不会倒, 因为第二块没有倒。 "推倒" 这一过程早已在第一和第二块之间就中断了。

通俗点来说就是k = 1时结论不成立。因为当k = 1时，k+1为2，此时假设两匹马的编号分别为1,2,去掉编号为K+1的马后得不到“编号为2的马与编号为1的马颜色相同”的结论。去掉1后，只剩2，自己和自己同色；去掉2后，只剩1，自己和自己同色，始终无法退出1和2同色的结论。但当k>1时，以上证明是成立的。

参考资料：数学归纳法: 所有的马颜色相同? - 知乎

鸽巢原理

n个物品分成r*m份(n>rm)，至少有一份数量是>=r+1的

Execise:

There is an element in the sequence 7, 77, 777, 7777, ⋯, that is divisible by 2003.

利用反证法+鸽巢原理

1.假设序列都不能被2003整除，那他们一定除以2003时有余数，余数范围在1~2002之间，一共有2003种余数，但序列的项数是无穷的（大于2003），所有一定有两项的余数是相等的2.设这两位为Ai和Aj(i<j),那么2003 | Aj-Ai，结果形式为777...700...0;假设有x个7和y个0，那么可以写成77777...7*10^(y)的形式，因为2003是素数，无法整除10的y次方，所以整除2003的一定是前面的777...777，所以可以找到一个整除2003的序列

3.推出的结论与我们假设的前提矛盾，故假设不成立，一定能找到被2003整除的项

容斥原理

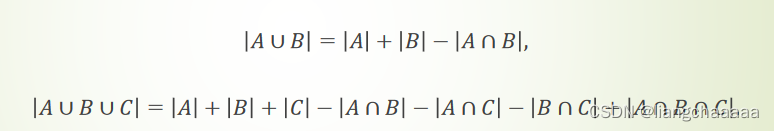
Execise
How many positive integers in [105] ({1,2, ⋯ , 105}) that have factor 3 or 5 or 7?

1.用容斥原理做：35+21+15-7-5-3+1 = 57

2.用欧拉定理做，φ(105) = 105*(1-1/3)*(1-1/5)*(1-1/7) = 48; 105 - 48 = 57

Derangement（错排问题）

换一个等价问题：n 封不同的信与n个不同的信封 , 将 n封信都装错信封的方案个数 ;

考虑一个有n个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，那么这样的排列就称为原排列的一个错排。

错排公式中使用 D (n)表示n个元素的错排 ;

D (1) = 0

D (2) = 1 // B A

D (3) = 2 //B C A and C A B

...

公式推导

1.使用分步计数原理 , 先统计第一封信的排列方法 , 然后再讨论其余信的排列方法数，如首先找出一封信a出来 , 这封信不能排在其本身位置 , 只能放在其余n−1个位置上 , 因此有n−1种排法 ;

2.使用分类计数原理，假设第一封信a占据了b的位置 , 那么此时b放在哪个信封分两种情况 , b放在 a位置 , 或b不放在a位置 ;

b放在了a的位置，方案数为D(n-2)

b没放在a的位置，那么b可能出现在除a之外的任何位置 ,b有 n−2 个位置可以去 , 不能去a和b的位置 , 其余所有元素都有n−2个位置可以去，这种情况下相当于除a之外的其它元素的错排问题 , 即n−1个元素的错排问题 , 方案数是 D(n−1) ;

D(n) = (n-1)(D(n-1)+D(n-2))

D(1) = 0,D(2) = 1,可迭代求出方案数

或者使用生成函数求出递推方程：

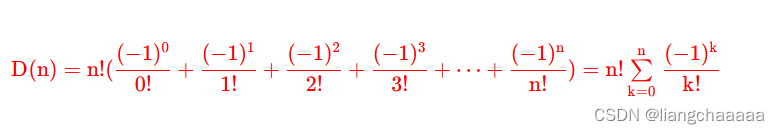
排列与阶乘

Execise
A gardener has 3 blue flowers, 4 red flowers and 5 white flowers to plant in a
row. In how many different ways can she do that?

(3+4+5)! / 3!*4!*5!

因为3种花是相同的，怎么摆都算一种，所以要除以3*2*1种不同的摆放方法，视为同一情况

函数映射

单射(injection):每一个x都有唯一的y与之对应

满射(surjection):每一个y都必有至少一个x与之对应，

双射(又叫一一对应,bijection): 同时满足单射与满射

组合

Execise
A worker has to work for 6 days in May.However, he is not allowed to work two consecutive days.In how many different ways can he choose the 6 days he will work