---

738.单调递增的数字

教程视频：https://www.bilibili.com/video/BV1Kv4y1x7tP/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891

从后向前遍历，一旦前一个数大于后一个数（非递增情况），将前一位数减一，后一位及其之后的数全都变成9。
【注意】
1、不要从前向后遍历，因为数字会变小，不能总是保证前面遍历过的结果保持递增。只有从后向前遍历才能重复利用上次比较的结果。
2、一旦有一位减一后，其后所有位都要变为9，才能保证数值最大，这里只要记录9的最高位。（贪心）

class Solution {
    public int monotoneIncreasingDigits(int n) {
        String s = n+"";
        char[] c = s.toCharArray();
        int index = c.length;
        for(int i=c.length-1;i>0;i--){
            if(c[i-1]>c[i]){
                c[i-1]=(char)(c[i-1]-1);
                index = i;
            }
        }
        for(int i=index;i<c.length;i++){
            c[i]='9';
        }
        n=0;
        for(int i=0;i<c.length;i++){
            n=n*10+(c[i]-'0');
        }
        return n;
        //利用api，耗时耗空间
        //return Integer.parseInt(String.valueOf(c));
    }
}

---

968.监控二叉树（难）

教程视频：https://www.bilibili.com/video/BV1SA411U75i/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891


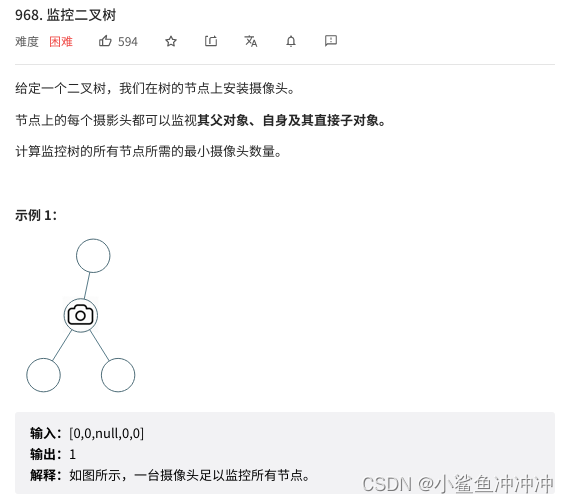
最开始的贪心思路有两种：1、根结点下一层方摄像头；2、叶子节点上一层放摄像头。考虑叶子节点数量远大于根结点数量，省下的摄像头数量更多i，因此采用思路2。

局部最优： 让叶子节点的父节点安摄像头，所用摄像头最少。
整体最优： 全部摄像头数量所用最少！

大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

此时需要确定二叉树的遍历方式，分析后发现当前节点状态需要根据其叶子节点状态推出，因此采用后序（左右中）遍历。

同时，设置三个数字来表示节点当前状态：（注意0和2状态之和即为无摄像头状态，不需要在额外设置无摄像头状态）
0：该节点无覆盖（无摄像头）
1：本节点有摄像头
2：本节点有覆盖（无摄像头）

递归终止条件（空节点状态认定）：为了保证叶子节点上层节点安装摄像头，空节点应该向上层返回状态2（本节点有覆盖）。

最后考虑递归处理逻辑，节点状态共有四种：

1. 情况1：左右节点都有覆盖，当前节点返回无覆盖状态，使其上一节点进入情况2；
2. 情况2：左右节点至少有一个无覆盖的情况，当前节点应该安装摄像头，摄像头+1，返回状态1；
3. 情况3：左右节点至少有一个有摄像头，当前节点返回状态2；
4. 情况4：头结点没有覆盖，这个情况最后在主函数中讨论。

【注意】当左右子节点状态为1和0时，应该进入情况情况2的逻辑，给当前节点安装摄像头，因此情况2的判断应该放在情况3前面。

class Solution {
    int camera=0;
    public int minCameraCover(TreeNode root) {
        //情况4
        if(traversal(root)==0){
            camera++;
        }
        return camera;
    }

    int traversal(TreeNode node){
        if(node==null)return 2;

        int left = traversal(node.left);//左
        int right = traversal(node.right);//右
        //中
        //情况1
        if(left==2 && right ==2)return 0;
        情况2
        if(left==0 || right==0){
            camera++;
            return 1; 
        }
        //情况3
        if(left == 1 || right ==1)return 2;
        return -1;//不会走到这条，仅为满足语法需要
    }
}

---