介绍: 在二叉搜索树的前提下,左右高度差(平衡因子)的绝对值不大于1

二叉搜索数->中序排序树->极端情况下时间复杂度高 ->我博客更过不了解去翻翻

(搜索二叉树——寻找节点，插入节点，删除节点_别想闲鱼了！快去学习的博客-CSDN博客)

平衡因子=右树高度-左树高度

写一下AVL的插入操作

首先就是 插入新的数 -> 流程就是二叉搜索数插入方式

 // 像搜索二叉树的操作插入
        TreeNode node = new TreeNode(val);
        if(root==null){
            root = node;
            return true;
        }

        TreeNode parent =  null;
        TreeNode cur = root;
        while (cur!=null){
            if(cur.val > val){
                parent = cur;
                cur = cur.left;
            } else if(cur.val == val){
                return false;
            } else {
                parent = cur;
                cur = cur.left;
            }
        }
        if(parent.val>val){
            parent.left = node;
        } else {
            parent.right = node;
        }
        node.parent = parent;
        cur = node;

调节一下平衡因子

 // 调节平衡因子
        while (parent != null){
            // 检查左右
            if(cur == parent.right){
                parent.bf++;
            }else {
                parent.bf--;
            }
            // 检查平衡因子
            if(parent.bf==0){
                // 平衡
                break;
            } else if(parent.bf==1 || parent.bf==-1){
                // 继续向上修改
                cur = parent;
                parent = cur.parent;
            } else {
                // 不是高度差绝对值小于1了 进行调整
                if(parent.bf==2){
                    if(cur.bf==1){
                        // 左旋
                        rotateLeft(parent);
                    } else{
                        // cur.bf==-1
                        rotateRL(parent);
                    }
                } else {
                    if(cur.bf==-1){
                        // 右旋
                        rotateRight(parent);
                    } else{
                        // cur.bf==1
                        rotateLR(parent);
                    }
                }
                break;
            }
        }

okk重点操作 左旋情况 

parent.bf==2

cur.bf==1

 

 

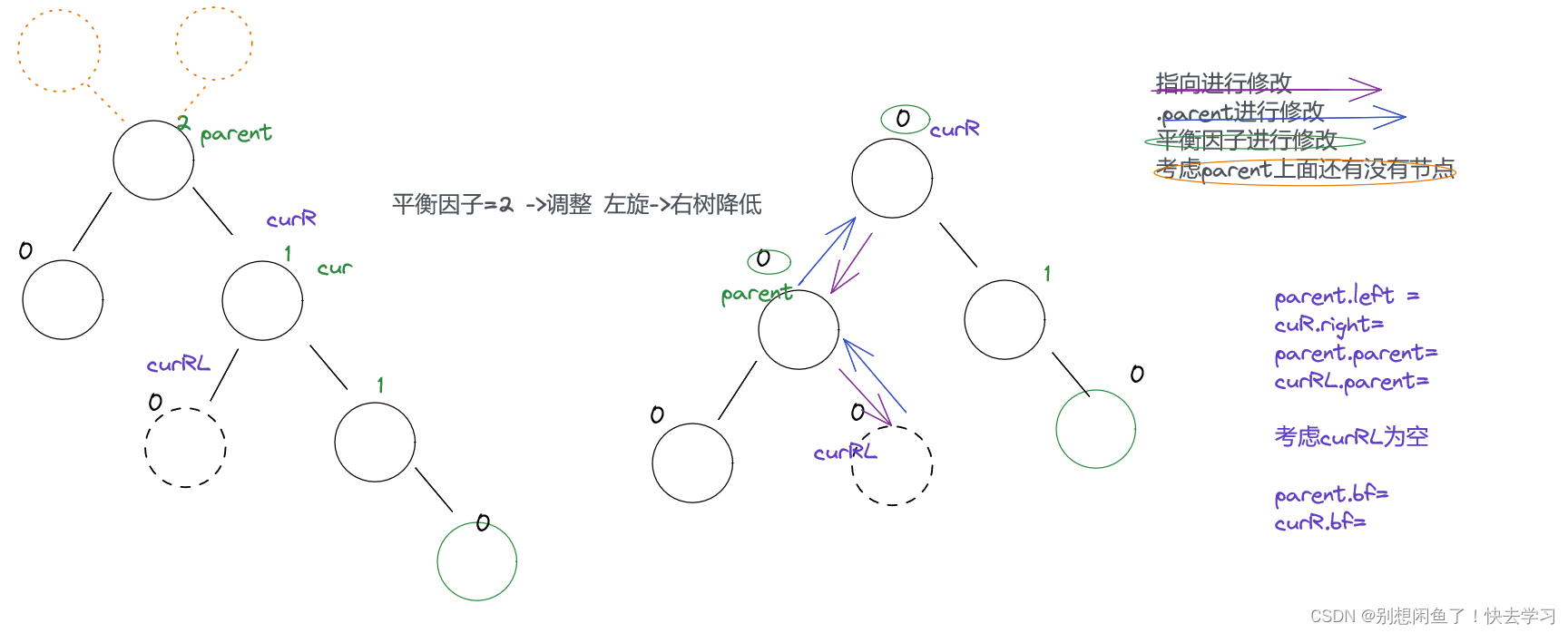
private void rotateLeft(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        subR.left = parent;
        parent.right = subRL;
        if(subRL != null){
            subRL.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subR;
        if(parent==root){      
            root = subR;
            root.parent = null;
        } else {
            if(pParent.left==parent){
                pParent.left = subR;
            } else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }


        subR.bf = 0;
        parent.bf = 0;

    }

当然右旋也同理可得~~~

我们再来看 左右旋

parent.bf==-2

cur.bf==1

 

 

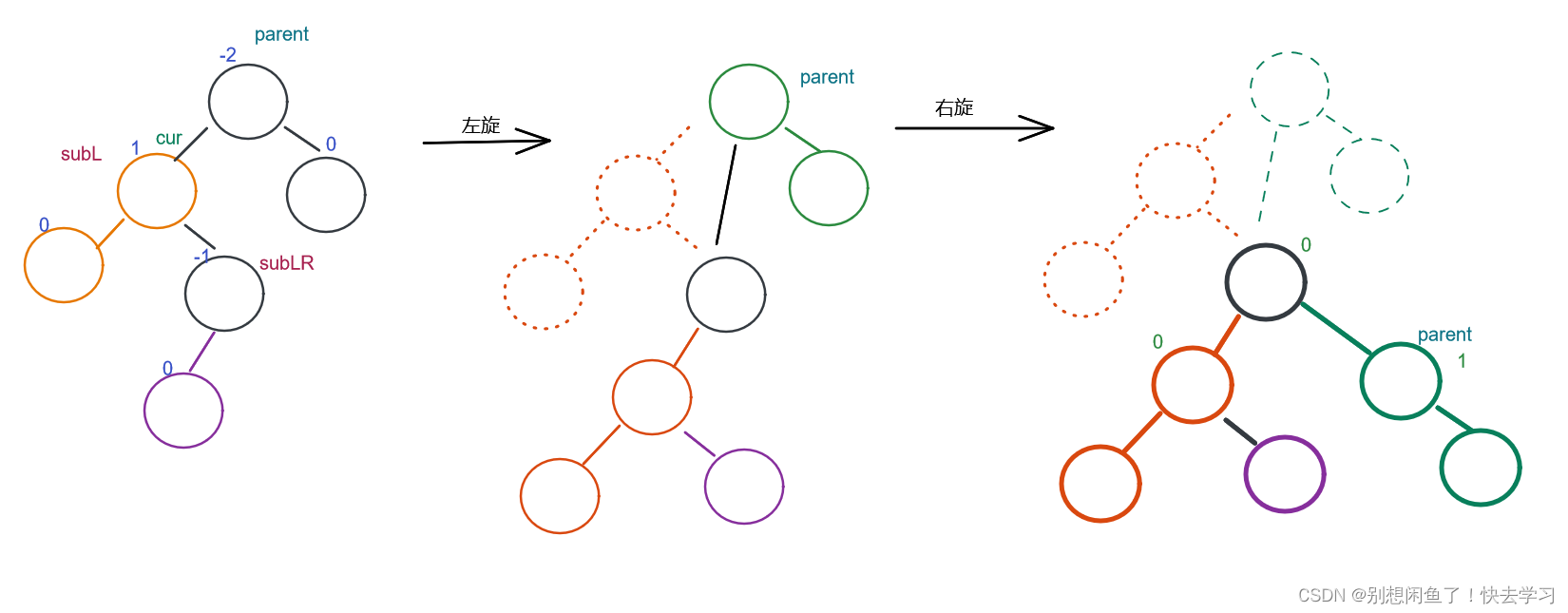
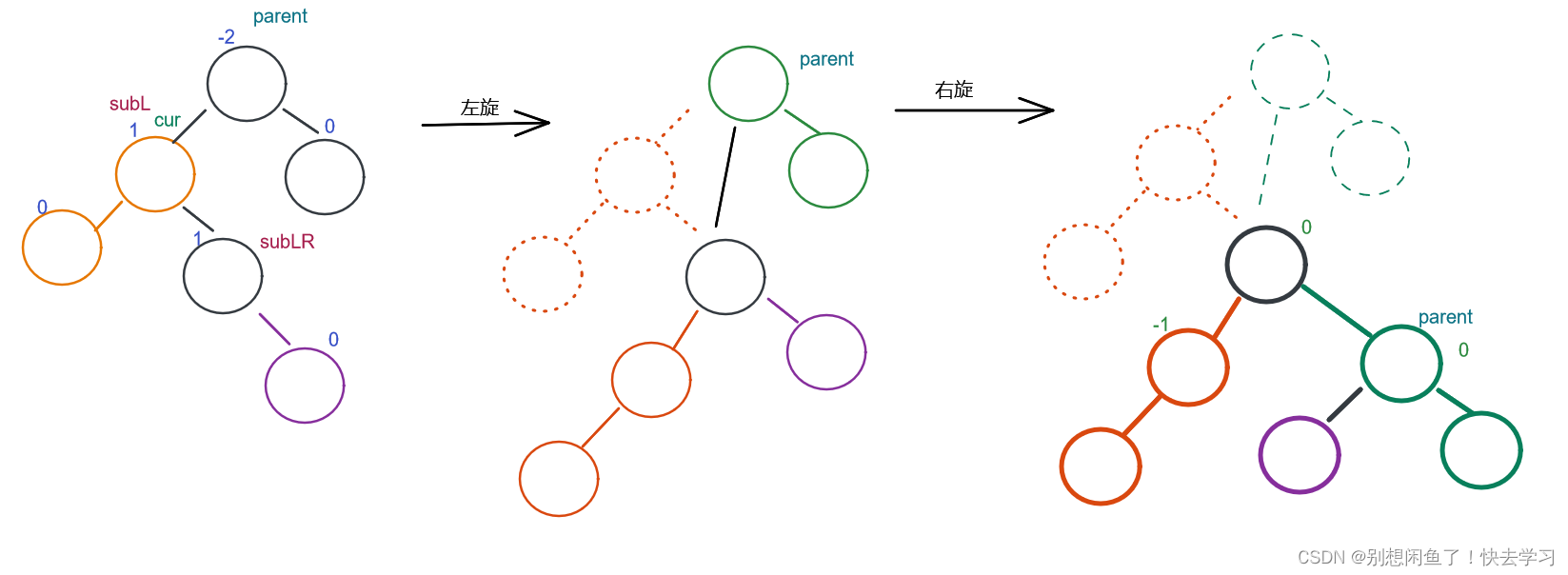
 所以可以看出 平衡因子修改还要有限制条件~~~(subLR)

private void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;

        rotateLeft(subL);
        rotateRight(parent);

        if(bf==1){
            subL.bf = -1;
            parent.bf = 0;
        }else if(bf==-1){
            subL.bf = 0;
            parent.bf = 1;
        }

        subLR.bf = 0;

    }