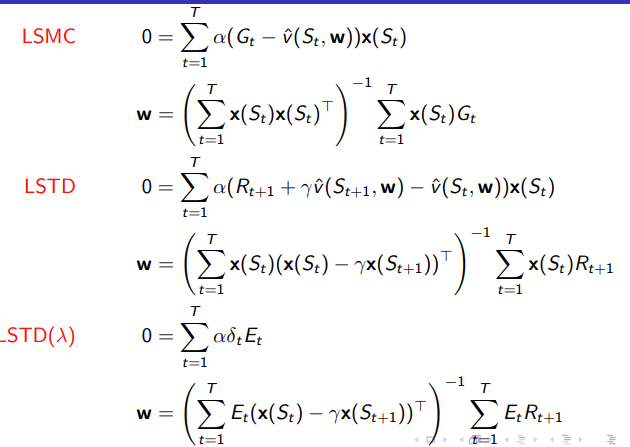1 Introduction
pipeline大致讲完了,开始到数值计算的部分。
1.1 大规模的运算

对于这种大规模运算,如何拓展前面两个章节的内容,进行实战。
1.1.1 回顾value function approximation

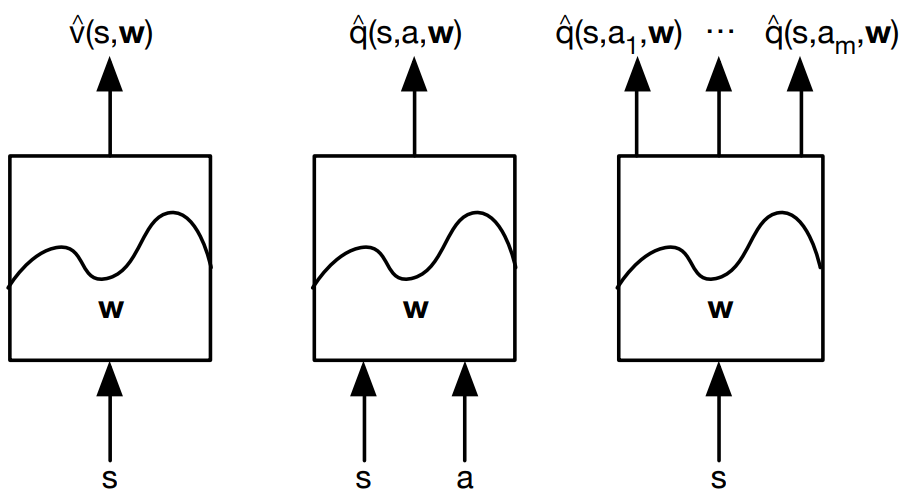
1.1.3 which function approximator
强化学习中的值函数近似(value function approximation)是一种用于估计值函数(如状态值函数V或状态动作值函数Q)的方法。它的主要作用是在大型或连续状态空间的强化学习问题中提供可扩展的解决方案。值函数近似通过将值函数表示为参数化的函数形式(如线性模型、神经网络、决策树等),可以减少存储和计算需求,从而使得算法在大型和复杂的环境中仍然有效。
线性值函数近似:在这种方法中,值函数用一个线性函数表示,即 V ( s ) = θ T ⋅ ϕ ( s ) V(s) = \theta^T \cdot \phi(s) V(s)=θT⋅ϕ(s) 或 Q ( s , a ) = θ T ⋅ ϕ ( s , a ) Q(s,a) = \theta^T \cdot \phi(s,a) Q(s,a)=θT⋅ϕ(s,a),其中 θ \theta θ 是参数向量, ϕ ( s ) \phi(s) ϕ(s) 和 ϕ ( s , a ) \phi(s,a) ϕ(s,a) 分别是状态特征向量和状态-动作特征向量。通过调整参数向量 θ \theta θ,我们可以拟合值函数。在线性值函数近似中,特征向量的选择至关重要,因为它们决定了能否有效地表示值函数。

需要训练方法,适用于non-stationary, non-iid 数据。
下面是一个用线性函数表示Q-table的frozenlake的例子
Q
(
s
,
a
)
=
θ
T
⋅
ϕ
(
s
,
a
)
Q(s,a) = \theta^T \cdot \phi(s,a)
Q(s,a)=θT⋅ϕ(s,a)
import numpy as np
import gym
# 定义状态-动作对到特征向量的映射函数
def state_action_to_feature_vector(state, action):
num_states = env.observation_space.n
num_actions = env.action_space.n
feature_vector = np.zeros(num_states * num_actions)
index = state * num_actions + action
feature_vector[index] = 1
return feature_vector
# 初始化环境
env = gym.make('FrozenLake-v1')
num_states = env.observation_space.n
num_actions = env.action_space.n
# 初始化参数向量
theta = np.zeros(num_states * num_actions)
# 超参数
num_episodes = 5000
alpha = 0.01
gamma = 0.99
epsilon = 0.1
# 开始训练
for episode in range(num_episodes):
state = env.reset()
if isinstance(state, tuple):
state = state[0]
done = False
while not done:
# 使用 epsilon-greedy 策略选择动作
if np.random.rand() < epsilon:
action = env.action_space.sample()
else:
q_values = [np.dot(theta, state_action_to_feature_vector(state, a)) for a in range(num_actions)]
action = np.argmax(q_values)
# 采取动作,观察结果
next_state, reward, done, _, _ = env.step(action)
# 计算目标值
if done:
target = reward
else:
next_q_values = [np.dot(theta, state_action_to_feature_vector(next_state, a)) for a in range(num_actions)]
target = reward + gamma * np.max(next_q_values)
# 更新参数向量
theta += alpha * (target - np.dot(theta, state_action_to_feature_vector(state, action))) * state_action_to_feature_vector(state, action)
state = next_state
# 测试学习到的策略
num_test_episodes = 100
num_success = 0
for episode in range(num_test_episodes):
state = env.reset()
done = False
while not done:
q_values = [np.dot(theta, state_action_to_feature_vector(state, a)) for a in range(num_actions)]
action = np.argmax(q_values)
state, reward, done, _, _ = env.step(action)
if reward == 1.0:
num_success += 1
print(f"成功完成 {num_success} 次测试")
env.close()
对比之前的基于q_table的代码:
import numpy as np
import gym
# 初始化环境
env = gym.make('FrozenLake-v1')
# 初始化参数
n_states = env.observation_space.n
n_actions = env.action_space.n
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 0.1 # Epsilon-greedy策略参数
episodes = 20000 # 迭代次数
# 初始化Q表
q_table = np.zeros((n_states, n_actions))
# Epsilon-greedy策略
def epsilon_greedy_policy(state, q_table, epsilon):
if np.random.rand() < epsilon:
return np.random.randint(n_actions)
else:
return np.argmax(q_table[state])
# 通过重要性采样更新Q值
def update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon):
# 使用Q-Learning选择下一个动作
next_action = np.argmax(q_table[next_state])
# 使用Epsilon-greedy策略选择下一个动作
behavior_next_action = epsilon_greedy_policy(next_state, q_table, epsilon)
# 计算目标策略和行为策略的概率
target_policy_prob = 1.0 if action == next_action else 0.0
behavior_policy_prob = 1 - epsilon + epsilon / n_actions if action == behavior_next_action else epsilon / n_actions
# 计算重要性采样比率
importance_sampling_ratio = target_policy_prob / behavior_policy_prob
# 计算TD目标和TD误差
td_target = reward + gamma * q_table[next_state, next_action]
td_error = td_target - q_table[state, action]
# 使用重要性采样更新Q值
q_table[state, action] += alpha * importance_sampling_ratio * td_error
# 开始学习
for episode in range(episodes):
state = env.reset()
done = False
while not done:
# 选择动作
action = epsilon_greedy_policy(state, q_table, epsilon)
# 执行动作并观察结果
next_state, reward, done, _ = env.step(action)
# 更新Q表
update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon)
# 更新状态
state = next_state
print("Q-Table:")
print(q_table)
比较核心代码的区别
## q-table code
action = epsilon_greedy_policy(state, q_table, epsilon)
# 执行动作并观察结果
next_state, reward, done, _ = env.step(action)
# 使用Q-Learning选择下一个动作
next_action = np.argmax(q_table[next_state])
# 计算TD目标和TD误差
td_target = reward + gamma * q_table[next_state, next_action]
td_error = td_target - q_table[state, action]
# 使用重要性采样更新Q值
q_table[state, action] += alpha * td_error
# 更新状态
state = next_state
在Q-table方法中,我们维护了一个表格,其中每个状态-动作对都有一个对应的值。在值函数近似的方法中,我们试图找到一个参数向量 θ \theta θ,使得线性模型能够近似地表示状态-动作值函数。
在线性值函数近似方法中,我们尝试通过学习参数向量 θ \theta θ来逼近真实的Q值。实际上, θ \theta θ的作用类似于Q-table的作用,但它是一个连续的、可微的表示。我们使用梯度下降法来更新 θ \theta θ,以最小化预测值和实际值之间的误差。
请注意,虽然
θ
T
⋅
ϕ
(
s
,
a
)
\theta^T \cdot \phi(s, a)
θT⋅ϕ(s,a)和Q-table方法中的
Q
(
s
,
a
)
Q(s, a)
Q(s,a)都表示状态-动作值,但它们的表示和计算方式是不同的。Q-table方法使用离散的查找表表示Q值,而线性值函数近似方法使用线性模型和参数向量
θ
\theta
θ表示Q值。
在frozenLake这个例子中,因为状态向量是单位向量
feature_vector = np.zeros(n_states)
feature_vector[state] = 1
if np.random.uniform(0, 1) < epsilon:
return env.action_space.sample()
else:
q_values = [np.dot(theta, state_to_feature_vector(state)) for a in range(env.action_space.n)]
return np.argmax(q_values)
next_state, reward, done, _ = env.step(action)
global theta
current_value = np.dot(theta, state_to_feature_vector(state))
next_value = np.dot(theta, state_to_feature_vector(next_state))
td_target = reward + gamma * next_value
td_error = td_target - current_value
theta += alpha * td_error * state_to_feature_vector(state)
2 Incremental methods
2.1 gradient descent
使用增量方法(如梯度下降)可让我们逐渐优化值函数近似。在每个时间步,我们都会收到新的观测数据,使用TD目标和梯度下降来更新我们的参数。这样,在训练的过程中,我们的值函数近似将逐渐变得更加准确。这种增量方法的好处在于它能够在线地学习,而无需等待整个数据集收集完毕。
增量方法(如梯度下降)的关键优势在于它们能够处理不断变化的数据。强化学习中,智能体与环境的交互持续生成新的数据。使用增量方法,我们可以逐步更新我们的值函数近似,并逐步改进我们的策略。这种在线学习方法使得智能体能够适应不断变化的环境,并持续优化其行为。
import numpy as np
import gym
def state_action_to_feature_vector(state, action, num_states, num_actions):
feature_vector = np.zeros(num_states * num_actions)
feature_vector[state * num_actions + action] = 1
return feature_vector
env = gym.make('FrozenLake-v1')
num_states = env.observation_space.n
num_actions = env.action_space.n
theta = np.random.randn(num_states * num_actions)
num_episodes = 5000
alpha = 0.01
gamma = 0.99
epsilon = 0.1
for episode in range(num_episodes):
state = env.reset()
done = False
while not done:
if np.random.rand() < epsilon:
action = env.action_space.sample()
else:
q_values = [np.dot(theta, state_action_to_feature_vector(state, a, num_states, num_actions)) for a in range(num_actions)]
action = np.argmax(q_values)
next_state, reward, done, _ = env.step(action)
if done:
target = reward
else:
next_q_values = [np.dot(theta, state_action_to_feature_vector(next_state, a, num_states, num_actions)) for a in range(num_actions)]
target = reward + gamma * np.max(next_q_values)
theta += alpha * (target - np.dot(theta, state_action_to_feature_vector(state, action, num_states, num_actions))) * state_action_to_feature_vector(state, action, num_states, num_actions)
state = next_state
体现gradient descent部分如下
next_q_values = [np.dot(theta, state_action_to_feature_vector(next_state, a, num_states, num_actions)) for a in range(num_actions)]
target = reward + gamma * np.max(next_q_values)
loss = (target - np.dot(theta, state_action_to_feature_vector(state, action, num_states, num_actions)))
gradient = - state_action_to_feature_vector(state, action, num_states, num_actions)
theta += -alpha * loss * gradient
# 对比之前不适用gradent descent的代码
current_value = np.dot(theta, state_to_feature_vector(state))
next_value = np.dot(theta, state_to_feature_vector(next_state))
td_target = reward + gamma * next_value
td_error = td_target - current_value
theta += alpha * td_error * state_to_feature_vector(state)
在强化学习中,我们通常使用Temporal Difference(TD)目标作为实际目标值。TD目标是当前奖励加上折扣后的未来预测值。TD误差表示为:
ϕ t = R t + 1 + γ v ^ ( S t + 1 , w ) − v ^ ( S t , w ) \phi_t=R_{t+1} + \gamma \hat{v}(S_{t+1}, \bm{w}) -\hat{v}(S_t, \bm{w}) ϕt=Rt+1+γv^(St+1,w)−v^(St,w)其中 δ t \delta_t δt是TD误差, R t + 1 R_{t+1} Rt+1是下一个时间步的奖励, γ \gamma γ是折扣因子, v ^ ( S t , w ) \hat{v}(S_t, \boldsymbol{w}) v^(St,w)是当前状态值函数的预测值, v ^ ( S t + 1 , w ) \hat{v}(S_{t+1}, \boldsymbol{w}) v^(St+1,w)是下一个状态值函数的预测值, w \boldsymbol{w} w是值函数近似的参数向量。
对于刚才那个例子
L ( θ ) = 1 2 ( t a r g e t − Q ( s , a ) ) 2 L(\theta)=\frac{1}{2}(target - Q(s,a))^2 L(θ)=21(target−Q(s,a))2
∂ L ( θ ) ∂ θ = ( t a r g e t − Q ( s , a ) ) ∗ ( − ϕ ( s , a ) ) \frac{\partial L(\theta)}{\partial \theta} = (target-Q(s,a))*(-\phi(s,a)) ∂θ∂L(θ)=(target−Q(s,a))∗(−ϕ(s,a))

通过stochastic gradient descent 进行value function approximation
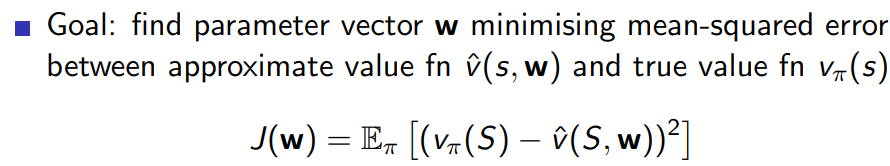
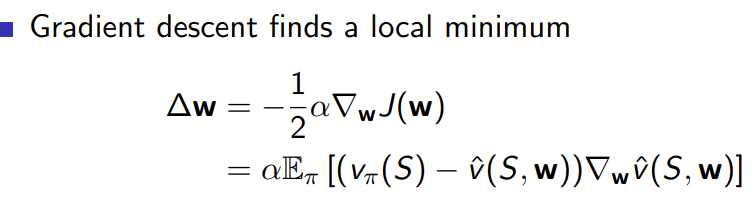
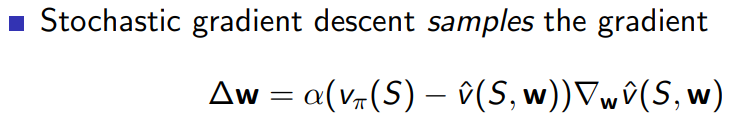

2.2 Feature Vectors
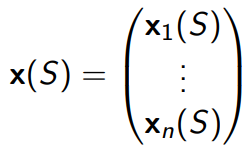

2.2.1 Linear Value function Approximation

2.2.2 table lookup features
实现了前面线性拟合q-table的例子


- 在monte-carlo中使用value function approximation

- TD-learning with value function approximation

- TD(λ) with Value Function Approximation

在control的时候,使用q值代替v值

- Linear action-value function approximation


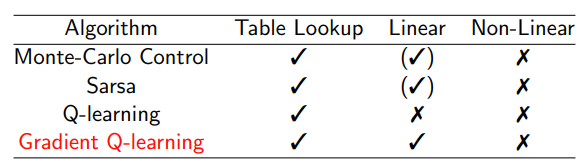
2.3 convergence
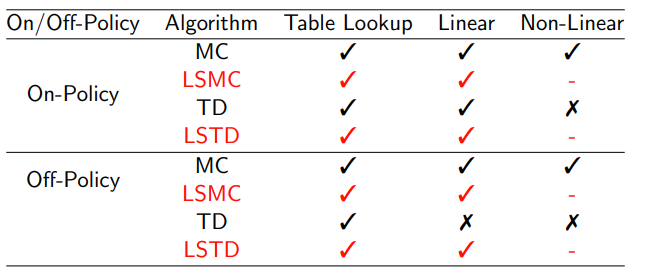
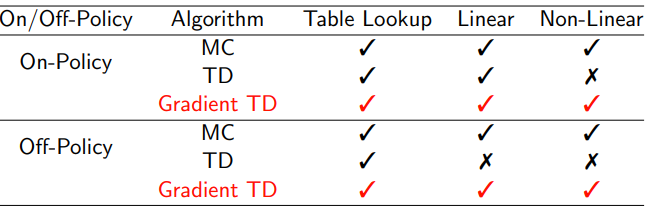
2.3.1 convergence of prediction algorithms
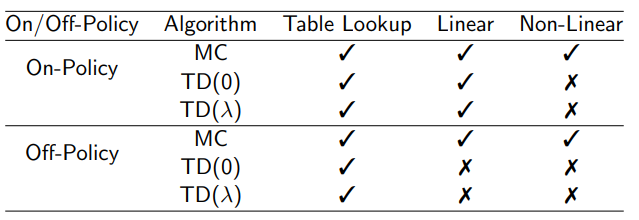
TD does not follow the gradient of any objective function
This is why TD can diverge when off-policy or using
non-linear function approximation
Gradient TD follows true gradient of projected Bellman error
3 Batch Methods
batch methods的意义

3.1 least squares prediction
3.1.1 Least Squares Prediction
通过Least squares的算法找到参数vector w, 最小化
v
^
(
s
t
,
w
)
\hat{v}(s_t, \bm{w})
v^(st,w)和target value
v
t
π
v_t^{\pi}
vtπ的误差
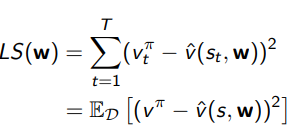
3.1.2 Stochastic Gradient Descent with Experience Replay

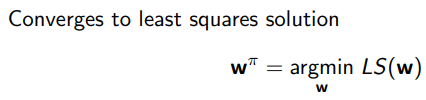
用least-square去拟合值函数,解决frozenlake的问题
- 数据集采集的方法,数据采集策略的选择对学习结果至关重要。如果数据集没有足够的多样性或没有充分探索状态空间,那么学到的策略可能会受到限制。这就是为什么在数据采集阶段,一种平衡探索和利用的策略可能是更好的选择。
- 随机策略:在这种策略下,智能体在每个状态下都随机选择动作。这种策略可以确保环境的充分探索,但可能无法充分利用已学到的知识。
- 贪心策略: 这种策略下,智能体始终选择具有最高估计动作值的动作。这种策略充分利用了已学到的知识,但可能在探索方面不足。
- ε-贪心策略: 这是一种介于随机策略和贪心策略之间的策略。在这种策略下,智能体以1-ε的概率选择具有最高估计动作值的动作,以ε的概率随机选择动作。这种策略在探索和利用之间进行权衡。
- 其他探索策略: 还有许多其他探索策略,如 UCB(Upper Confidence Bound)算法,它基于置信区间来平衡探索和利用。这些方法通常用于在线学习设置,但也可以用于生成数据集。
- 目标值:target = reward + gamma * np.max(next_q_values)
- 状态向量:这个里面采用的是,执行了动作,设置状态向量对应值为1
import numpy as np
import gym
def state_action_to_feature_vector(state, action, num_states, num_actions):
feature_vector = np.zeros(num_states * num_actions)
feature_vector[state * num_actions + action] = 1
return feature_vector
env = gym.make('FrozenLake-v1')
num_states = env.observation_space.n
num_actions = env.action_space.n
theta = np.zeros(num_states * num_actions)
num_episodes = 5000
alpha = 0.01
gamma = 0.99
epsilon = 0.1
# Collect a dataset of state-action pairs, rewards, and next states.
dataset = []
for episode in range(num_episodes):
state = env.reset()
done = False
while not done:
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
dataset.append((state, action, reward, next_state))
state = next_state
# Perform least squares fitting.
X = np.array([state_action_to_feature_vector(s, a, num_states, num_actions) for s, a, r, next_s in dataset])
y = np.array([r + gamma * np.max([np.dot(theta, state_action_to_feature_vector(next_s, next_a, num_states, num_actions)) for next_a in range(num_actions)]) if not done else r for s, a, r, next_s in dataset])
theta = np.linalg.lstsq(X, y, rcond=None)[0]
# Test the learned policy.
state = env.reset()
done = False
while not done:
q_values = [np.dot(theta, state_action_to_feature_vector(state, a, num_states, num_actions)) for a in range(num_actions)]
action = np.argmax(q_values)
next_state, reward, done, _ = env.step(action)
state = next_state
env.render()
3.1.3 Experience Replay in Deep Q-Networks
DQN uses experience replay and fixed Q-targets
使用DQN解决刚才这个frozenLake的问题

import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import random
from collections import deque
class DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DQN, self).__init__()
self.fc = nn.Linear(input_dim, output_dim)
def forward(self, x):
return self.fc(x)
def one_hot_encoding(state, num_states):
encoded_state = np.zeros(num_states)
encoded_state[state] = 1
return encoded_state
env = gym.make('FrozenLake-v1')
num_states = env.observation_space.n
num_actions = env.action_space.n
dqn = DQN(num_states, num_actions)
optimizer = optim.Adam(dqn.parameters(), lr=0.01)
loss_fn = nn.MSELoss()
num_episodes = 2000
epsilon = 0.1
gamma = 0.99
replay_buffer = deque(maxlen=10000)
for episode in range(num_episodes):
state = env.reset()
done = False
while not done:
if np.random.rand() < epsilon:
action = env.action_space.sample()
else:
state_tensor = torch.FloatTensor(one_hot_encoding(state, num_states)).unsqueeze(0)
q_values = dqn(state_tensor)
action = torch.argmax(q_values).item()
next_state, reward, done, _ = env.step(action)
# Store the transition in the replay buffer
replay_buffer.append((state, action, reward, next_state, done))
state = next_state
# Train the DQN with a random sample from the replay buffer
if len(replay_buffer) >= 64:
batch = random.sample(replay_buffer, 64)
states = torch.FloatTensor([one_hot_encoding(s, num_states) for s, a, r, next_s, d in batch])
actions = torch.LongTensor([a for s, a, r, next_s, d in batch]).unsqueeze(1)
rewards = torch.FloatTensor([r for s, a, r, next_s, d in batch]).unsqueeze(1)
next_states = torch.FloatTensor([one_hot_encoding(next_s, num_states) for s, a, r, next_s, d in batch])
dones = torch.BoolTensor([d for s, a, r, next_s, d in batch])
q_values = dqn(states).gather(1, actions)
target_q_values = rewards + gamma * dqn(next_states).max(1, keepdim=True)[0].detach()
target_q_values[dones] = rewards[dones]
loss = loss_fn(q_values, target_q_values)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test the learned policy
state = env.reset()
done = False
while not done:
state_tensor = torch.FloatTensor(one_hot_encoding(state, num_states)).unsqueeze(0)
q_values = dqn(state_tensor)
action = torch.argmax(q_values).item()
next_state, reward, done, _ = env.step(action)
state = next_state
env.render()
关键的要点
从代码上来看比较简单
q_values = dqn(states).gather(1, actions)
target_q_values = rewards + gamma * dqn(next_states).max(1, keepdim=True)[0].detach()
target_q_values[dones] = rewards[dones]
loss = loss_fn(q_values, target_q_values)
这个示例中的关键部分包括:
1. 定义一个简单的神经网络(`DQN` 类),它接收状态作为输入,并输出每个动作的 Q 值。
2. 使用经验回放缓冲区(`replay_buffer`)来存储智能体与环境交互过程中的经验。
3. 在每个时间步上,从经验回放缓冲区中随机采样一个批次的数据,并使用这些数据来训练神经网络。
4. 使用 ε-贪心策略来平衡探索与利用。
在完成训练后,我们使用训练好的神经网络来测试学到的策略。这个示例可能需要一些调整,才能在 FrozenLake-v1 环境中获得最佳性能。在实际应用中,对于更复杂的问题,我们通常会使用更复杂的神经网络结构,例如卷积神经网络(CNN)或循环神经网络(RNN),来表示 Q 函数。
4.2 linear least squares prediction