every blog every motto: There’s only one corner of the universe you can be sure of improving, and that’s your own self.
https://blog.csdn.net/weixin_39190382?spm=1010.2135.3001.5343

0. 前言

目标检测入门实战教程

1. 正文

1.1 感性认识

我们想做的事，其实并不复杂。说白了就是输入一张图，输出对应的有标框（标注对应的物体）的图。如下图所示：

更进一步，如下图所示，通过不断循环，以实现优化效果。

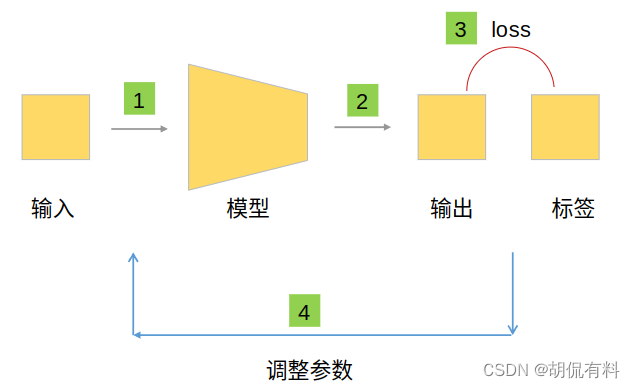
当我们训练完成（模型参数调整合适时），我们即可以直接用该模型：

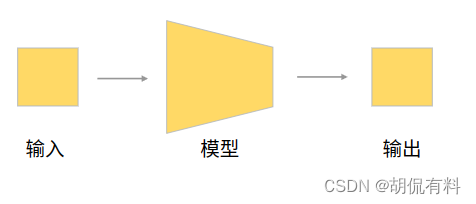
下图为网络的模型结构图：

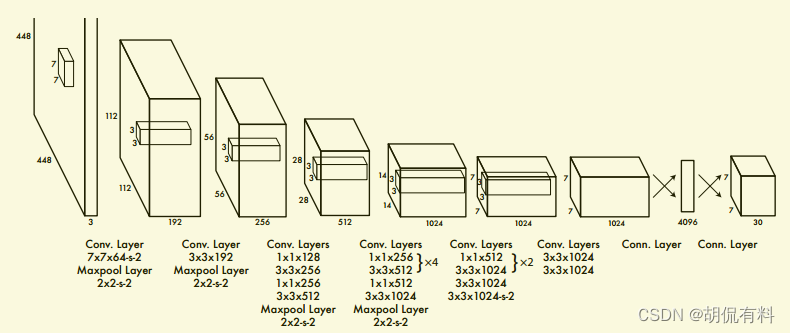
1.2 前提梗概

在网络中，一切都是以数据形式存在的，更具体是以“数组”的形式存在。

1.2.1 当我们谈“物体”落在某个格子中 ，就由那个格子负责，我们在谈什么？

要回答这个问题，我们先回答以下问题。

1.2.2 当我们谈“物体”的时候，我们在谈什么？

下图是算是“经典”示例图了，
当我们谈图中物体“狗”时，我们说的时“狗这个区域”，这是较为直观的理解。
反映在程序中，这一张图片是一个多维数组（三维，长宽和通道），所以，在程序中，体现的是狗这个区域在三维数组中的数值。

上述说的区域，是另一类任务，分割。在目标检测中，我们谈“物体”，我们谈的又是什么呢？

自然，是目标框，如下图所示，我们说到物体，本质还在说这个框，因为我们需要的也正是这个框。

反映在程序中，是这框的四个顶点（坐标），是的，在程序中我们由四个顶点也就确定了这个框。这个框还有另一种说法（表示）： 中心坐标，框的长宽，即**（x, y, w, h）**。

所以，当我们谈物体的时候，是在谈框（包围框，包围物体的框），是在谈四个顶点，更是在谈**（x, y, w, h）（中心表示法，行文称呼，不知道有没有统一规范的称呼）**

微小结： 当我们谈物体的时候，我们在谈(x,y,w,h)

1.2.3 当我们谈“格子”的时候，我们在谈什么？

在一个宽泛的世界中，我们需要坐标（系）进行定位，这不得不谈到，诸如，北京54，西安80坐标系，CGCS200等等，我们普通人更熟悉的经纬度。通过坐标（系），我们能够准确知道其位置。

那在程序，图片中，有坐标（系）吗？
答案是有的，坐标原点在图片左上角，x轴水平向右，y轴竖直向下，如下图所示：

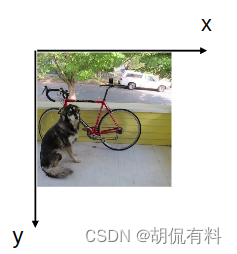
在上一小结中，我们已经将“狗”转换成（x,y,w,h）这种形式。这种表示更核心的是其坐标（x,y）,这个坐标可以在上面的坐标系下确定狗的位置。
现在，（理论上）可以对坐标进行预测了。why?
狗在图片有一个坐标（注意，我们这里说的中心坐标，即，狗包围框的中心坐标）。此外，在一张图片中有若干个物体，假设是n，预测的坐标m个(m>>n)，若图片大小为256，256，那么就有可能预测256*256个点。

那么，我们怎么知道预测的点是“狗”呢？换句话说，我们怎么让，狗的真实坐标和预测为狗的坐标进行损失计算呢？

这里是不知道的（严格来说可以知道，但计算起来依然不经济），比较可行的办法，是依次计算，那么就有n*m次运算，这还只是一次的计算过程，已经非常庞大了，在实际上是不可行的。

那么需要怎么做呢？

需要对预测的点进行筛选，或者说限定，进一步降低预测的个数，这样整个计算量会小很多。

像城市一样，划区，比如，高新区、经开区，通过这个区，也就知道一个人的大概位置了。
在图片中呢？没错就是，格子，只要告诉在第几行，第几列，也就知道了大概位置。

如下图所示，狗（注意：我们说的中心表示法，xywh）肯定会出现在一个格子里面，注意：这就是物体落子格子中 (一种“生动”的说法）

同时，这个格子里面也会预测若干个物体，这里假设为k个（k<<m）,

所以，这次的计算就是1k，（一个格子一条狗）这个数量是远远小于nm的。在实际计算中，也更加可行。（一个格子里面“落入”的物体（中心）可能不止一个，这个暂时不考虑）

这就是**“由这个格子负责预测狗”**，即，同样是种“生动”的说法，在深度学习中，类似这种“拟人”，“生动”的说法不胜枚举，诸如：“喂入数据”…，
搞明白了其本质也就那么一回事，各位读者自不必心生畏惧。

至此，我们也就知道了，物体落入格子，由那个格子负责预测究竟在说啥了。

1.3 究竟该怎么表示“狗”？

我们这里依然把模型当做黑盒，或是一个函数。对于一个函数，我们只需要把握输入和输出即可。

因为输出和标签要进行损失计算，自然，二者的形式（数组的形状，和每个位置代表的数值含义是一样的），所以我们要搞清楚标签是如何表示数据的。

对于上图的狗，我们知道狗“落”在其中一个格子中（注意：这里说的狗是包围框的中心）,那么我们这里也就确定了狗在哪了。比如下图，我们给狗所在的位置赋值3，也就是说狗和3这个值一一对应，其他物体再赋一个别的值，自然实现了区分。（为什么要赋值？因为在程序中一切都是数据，我们用3表示狗，回头预测的时候，在把3还原成“狗”这个汉字，也就好了）

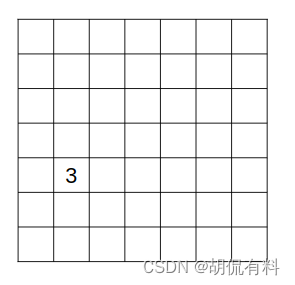
这样我们就能预测狗了吗？

注意，我们的目标是什么，是要预测是狗，更是狗这个包围框，而包围框在前文中，我们已经转换成x,y,w,h这种形式了。

上面只能预测位置（这个位置实际也是不对的），但是还缺少wh。细心地朋友可能发现了，上面是二维的，转成三维能够存储的数据也就多了。

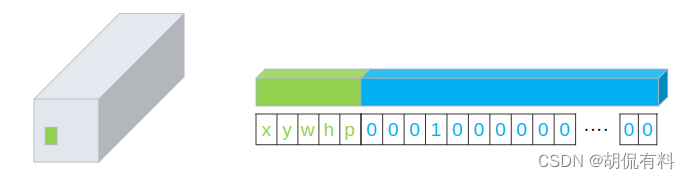
如下左图所示，狗的位置在绿色的格子中，我们将格子抽出来横着放，如右图所示。前5个分别放狗的中心坐标x,y，狗包围框的长宽，以及是不是狗（如果是是框，放1，不是框，放0）,后面20位是物体的one-hot编码。

这样我们就可以将这个框和这个框代表的类别完整表达出来。

我们预测值（输出）和真值，就可以计算二者之间的差距了（损失）。

在论文中，作者会预测两个框，每个框和真值计算IoU，结果大的代表我们预测的物体。

1.3 标签中的数值

在训练中，我们常将数据进行归一化，方便计算。对于图片，我们可以简单粗暴的将值除以255，缩放到0-1之间。那么对于标签我们怎么归一化呢？

对于类别，我们采用one-hot编码，对于置信度（或者说概率），采用0或1，现在就剩下x,y,w,h。
图片中的物体可能存在任何位置，且长宽不固定，对其归一化只需除以图片的长宽即可。

对于xy同样可以除以图片的长宽。但是还有更巧妙的办法，原始的xy是相对于原点（图片左上角），我们将其变换到相对于所在格子的左上角（可以理解为坐标变换），然后除以格子的长宽即可。

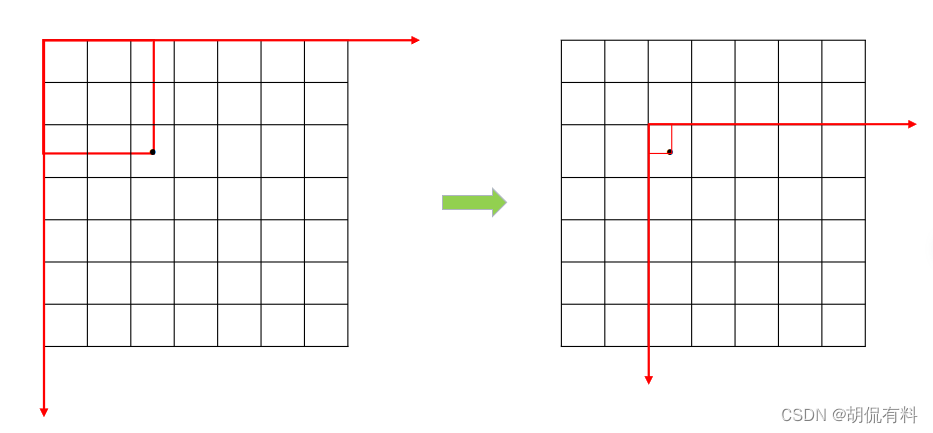
1.4 损失函数

对于标签，我们将数据组织如下形式，没有物体，所有值为0，有物体值为对应的值。如下图所示 ：

对于有物体来说，我们需要计算点坐标的差距（损失），长宽差距（损失），还有预测的概率，以及类型的差距（损失）。
我们这里的计算单元是格子，即每个格子中是否物体。论文中将图片划分成S×S的格子,S为7。

因为格子分为有物体和没有物体两种情况，所以损失也分为两种情况。
一张图片一般含有少数的物体。如上图的狗图片，含有狗、自行车、汽车三种物体。而我们的格子有49个。

所以对于有物体和没有物体损失的权重是不一样的。没有物体设置一个小的权重，有物体设置一个大一点的权重。即，
有物体则，
$${\lambda }_{coord}=5$$
否则，
$${\lambda }_{noobj}=0.5$$

1.4.1 有物体的情况

有物体的损失需要将以下四项相加

A. 坐标损失

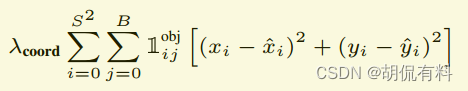
B. 长宽损失

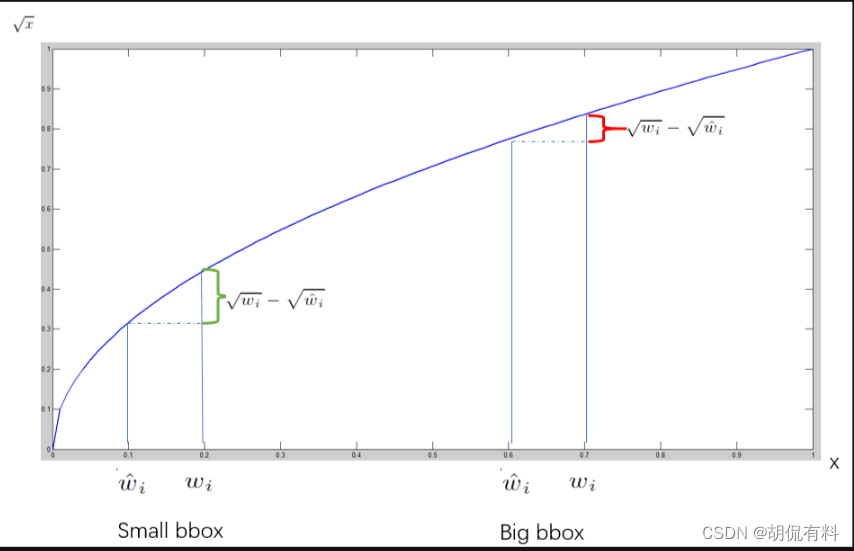
这里对长宽开根号，为什么？
如果没有开根号，
假如有一个小物体包围框为10×10，一个大物体包围框为100×100，他们的预测值和真值偏差都为2，那么损失为（不考虑前面的参数）：

$2^2+2^2=8$
即都为8，但是小框偏差2和大框偏差2严重程度是不一样的。

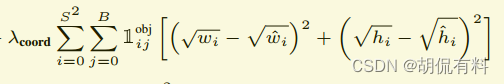
对小物体偏差要求会更严格，即损失会更大。

C. 置信度损失

具体后文会分析

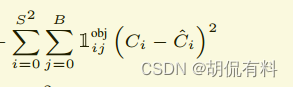
D. 类别损失

即对预测的类型计算损失

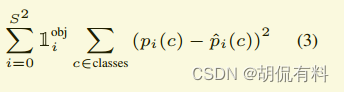
1.4.2 没有物体的情况

没有物体我们只需要计算置信度损失即可。

1.4.4 关于置信度的思考

说明： 为方便叙述和观察，以下只显示一个框，即B=1的情况

阅读过其他博客或是原论文的读者可能发现，我们在此前1.3节中将第五位设置成p，似乎和此前大部分博客中说的不同（就我看到的来说，都不相同）。究竟是咋回事？

大部分将第五位写作C，也就是置信度。如下图所示：

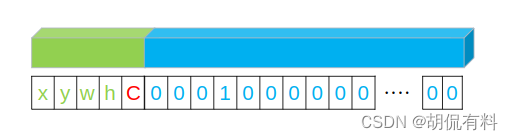
这种说法即对也不对。为什么？

–

说明： 对于一个值代表什么，我们要看他的标签代表什么，或者说在损失计算时候，他的标签（ground truth）代表什么。

1.4.4.1 部分误读：

在github的代码中，存在部分误读。将第五项当作置信度，如下图所示：

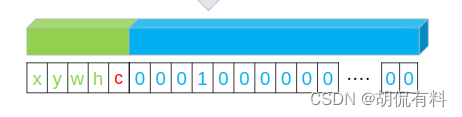
而我们在数据准备阶段时，是如下进行赋值的，即，

• 有物体，该值为1
• 没有物体，该值为0
  
  

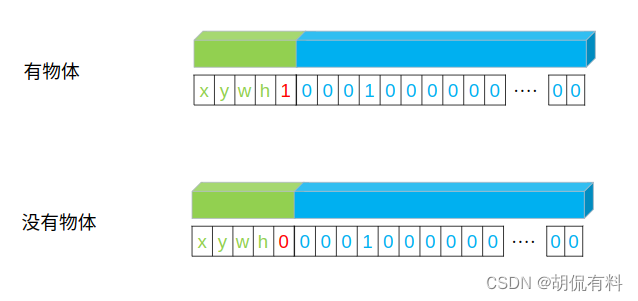
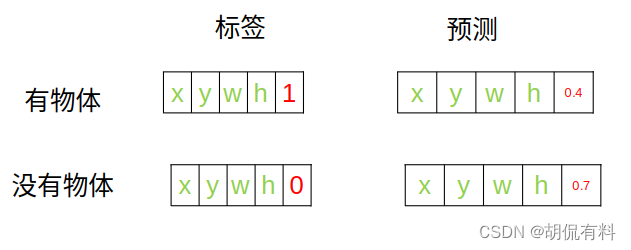
如果直接计算，
$$los{s}_{cof}=(C_i-{\hat{C}}_i{)}^2$$
即，
有物体：$(1-0.4{)}^2$
没有物体：$(0-0.7{)}^2$

这也是部分github代码中存在的一种写法，可是这对吗？我们看论文会发现，置信度是如下定义的：
$$confidence=Pr(object)\ast IO{U}_{pred}^{gt}$$

可以看到，置信度是预测概率和IOU的乘积，这里都没有用到IOU，而是把该值直接当做了置信度，自然是不对的。

实际在计算预测框的概率。

说明： 这中计算方式也是可行的，但不是论文中提到的置信度。

1.4.4.2 论文的表示：

说明： 下文中的“数据表示（准备）”指的是对标签的处理过程。
因为预测生成的数值，（刚开始）具有随机性，或者说，他只是一个值。其具体的含义要根据标签来定。

上述的这种错误实际是被论文中的表述所“误导”，论文中将第五项表述成置信度。

而实际上，这可以分为两部分。
第一部分是数据准备阶段。即将我们程序将本地数据加载到程序中的一种状态。
第二部分是实际使用阶段。即，在程序实际计算损失时候，第五项代表的含义。

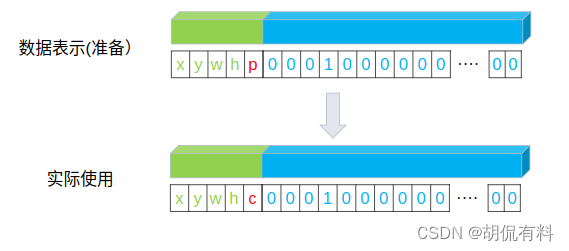
在实际计算时，比如某个格子里面有物体，那么p = 1，所以
$$confience=1\times IOU=IOU$$
所以，在实际使用ABCD各项代表的含义：

• 标签：A：IOU
• 预测：B: 预测的一个值， 0-1之间
• 标签：C: 0
• 预测：D: 预测的一个值，0-1之间

---

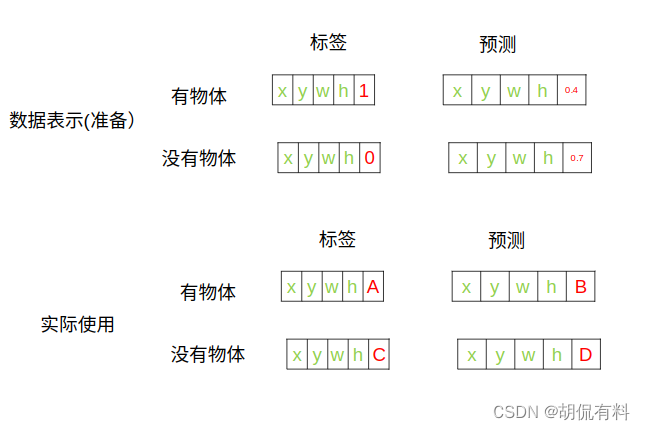
讨论：

1. 可能会有读者，感觉这第五项在计算好像没起作用， 实际上是起作用了，根据这一项，我们可以 将有物体的格子分在一组，没有物体的格子分在一组，然后分开计算，这就是我们前文提到的“负责”。
2. 但是，理论上我们可以根据xywh是否有值，也可进行这种划分：） （那么，还是没起作用？：））

---

那么在实际计算损失时,
有物体：$los{s}_{conf}=(A-B{)}^2$，即，
$$los{s}_{conf}=(IOU-pred{)}^2$$
没有物体：$los{s}_{conf}=(C-D{)}^2$，即，
$$los{s}_{conf}=(0-pred{)}^2$$

这部分和论文中描述的相同。

1.4.4.3 个人看法

笔者感觉可以将上述两种情况进行结合，或许效果会更好。

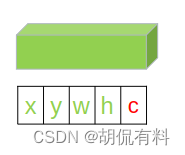
第五项放的是置信度。有物体为1，没有物体为0.（当然，可以看做是概率）

我们将预测的概率和IOU相乘，得到一个既包含概率，又包含对坐标点纠正的损失。

• 有物体时
  • 标签：A = 1
  • 预测：B = pr * IOU
• 没有物体时
  • 标签：C = 0
  • 预测：D = pr

如果没有物体时，我们标签中是没有框的，所以自然无法计算IOU，所以D=pr

但是，这样在公式方面就没法统一。有物体时，我们计算置信度，没有物体时，我们计算的预测概率。

1). 置信度损失的计算

通过上面，我们置信度这一项的损失有必要重新进行梳理。$los{s}_{cof}=(C_i-{\hat{C}}_i{)}^2$

A. 当有物体时

$los{s}_{conf}=(A-B{)}^2$， 即，
$$los{s}_{cof}=(1-pr\times IOU{)}^2$$

B. 当没有物体时

$los{s}_{conf}=(C-D{)}^2$，即，
$$los{s}_{cof}=(0-pr{)}^2$$

C. 小结

所以实际置信度损失，应该是：
有物体时：
$$los{s}_{cof}=(C_i-{\hat{C}}_i{)}^2$$
没有物体时：
$$los{s}_{cof}=(pr-{\widehat{pr}}_i{)}^2$$

没有物体时，我们用的应该是预测的概率，而不是置信度，因为没有IOU，所以没办法计算置信度。

1.4.4.4 小结

关于第五项，可以说有两套数据。第一套数据就是最开始的数据，或者说，数据准备时候的数据，他是我们我们制作标签的数据，同时，也是我们预测的数据。
第五项是概率：

但是在实际使用（计算损失），以及，论文表述时，会将第五项表述成置信度，这也就是我们常看到的。
第五项是置信度：
这是由公式转换而来。

---

至此，我们梳理了几个关键性的概念，接下来从代码层面进行分析。

1.5 代码

1.5.1 模型

模型的核心部分，图片从（448，448，3）变成（7，7，30）

def forward(self, x):
        # (448,448,3) -> (7,7,30)

        S, B, C = self.feature_size, self.num_bboxes, self.num_classes

        x = self.features(x) # (448,448,3) -> (14,14,1024)
        x = self.conv_layers(x) # (14,14,1024) -> (7,7,1024)
        x = self.fc_layers(x) # (7,7,1024) -> (1470)

        x = x.view(-1, S, S, 5 * B + C) # (1470) -> (7,7,30)
        return x

1.5.2 训练

训练部分核心代码

for epoch in range(num_epochs):
    print('\n')
    print('Starting epoch {} / {}'.format(epoch, num_epochs))

    # Training.
    yolo.train()
    total_loss = 0.0
    total_batch = 0

    for i, (imgs, targets) in enumerate(train_loader):
        # Update learning rate.
        update_lr(optimizer, epoch, float(i) / float(len(train_loader) - 1))
        lr = get_lr(optimizer)

        # Load data as a batch.
        batch_size_this_iter = imgs.size(0)
        imgs = Variable(imgs)
        targets = Variable(targets)
        imgs, targets = imgs.cuda(), targets.cuda()

        # Forward to compute loss.
        preds = yolo(imgs)
        loss = criterion(preds, targets)
        loss_this_iter = loss.item()
        total_loss += loss_this_iter * batch_size_this_iter
        total_batch += batch_size_this_iter

        # Backward to update model weight.
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

1.5.3 预测

部分核心代码

for i in range(S): # for x-dimension.
            for j in range(S): # for y-dimension.
                class_score, class_label = torch.max(pred_tensor[j, i, 5*B:], 0)

                for b in range(B):
                    conf = pred_tensor[j, i, 5*b + 4]
                    prob = conf * class_score
                    if float(prob) < self.prob_thresh:
                        continue

                    # Compute box corner (x1, y1, x2, y2) from tensor.
                    box = pred_tensor[j, i, 5*b : 5*b + 4]
                    x0y0_normalized = torch.FloatTensor([i, j]) * cell_size # cell left-top corner. Normalized from 0.0 to 1.0 w.r.t. image width/height.
                    xy_normalized = box[:2] * cell_size + x0y0_normalized   # box center. Normalized from 0.0 to 1.0 w.r.t. image width/height.
                    wh_normalized = box[2:] # Box width and height. Normalized from 0.0 to 1.0 w.r.t. image width/height.
                    box_xyxy = torch.FloatTensor(4) # [4,]
                    box_xyxy[:2] = xy_normalized - 0.5 * wh_normalized # left-top corner (x1, y1).
                    box_xyxy[2:] = xy_normalized + 0.5 * wh_normalized # right-bottom corner (x2, y2).

                    # Append result to the lists.
                    boxes.append(box_xyxy)
                    labels.append(class_label)
                    confidences.append(conf)
                    class_scores.append(class_score)

1.5.4 完整代码

待上传。。。

参考

[1] https://blog.csdn.net/weixin_39190382/article/details/126298644
[2] https://www.cnblogs.com/wangguchangqing/p/10406367.html
[3] https://blog.csdn.net/c20081052/article/details/80236015
[4] https://blog.csdn.net/weixin_43694096/article/details/123523225
[5] https://blog.csdn.net/m0_37192554/article/details/81092514
[6] https://zhuanlan.zhihu.com/p/70387154
[7] https://zhuanlan.zhihu.com/p/89143061
[8] https://blog.csdn.net/wjytbest/article/details/116116966#t7
[9] https://blog.csdn.net/hymn1993/article/details/122858410