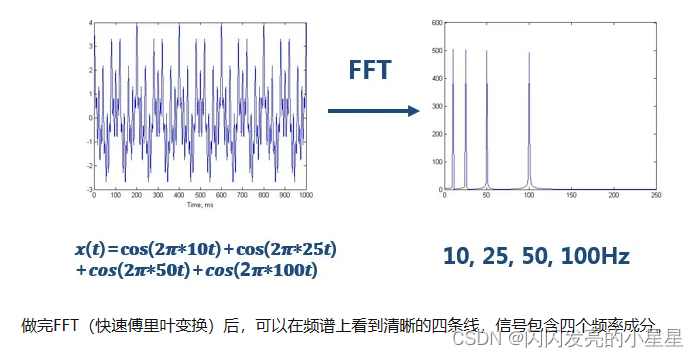
FFT
FFT 快速傅里叶变换,是利用计算机计算DFT的高效、快速计算的方法的统称。
将信号从时域变换到频域范围内。
matlab中的fft
- 语法:
Y = fft(X)
Y = fft(X,n)
Y = fft(X,n,dim)
- 说明
Y = fft(X) 用快速傅里叶变换 (FFT) 算法计算 X 的离散傅里叶变换 (DFT)。
*如果 X 是向量,则 fft(X) 返回该向量的傅里叶变换。
*如果 X 是矩阵,则 fft(X) 将 X 的各列视为向量,并返回每列的傅里叶变换。
*如果 X 是一个多维数组,则 fft(X) 将沿大小不等于 1 的第一个数组维度的值视为向量,并返回每个向量的傅里叶变换。
Y = fft(X,n) 返回 n 点 DFT。如果未指定任何值,则 Y 的大小与 X 相同。
- 如果 X 是向量且 X 的长度小于 n,则为 X 补上尾零以达到长度 n。
- 如果 X 是向量且 X 的长度大于 n,则对 X 进行截断以达到长度 n。
- 如果 X 是矩阵,则每列的处理与在向量情况下相同。
- 如果 X 为多维数组,则大小不等于 1 的第一个数组维度的处理与在向量情况下相同。
Y = fft(X,n,dim) 返回沿维度 dim 的傅里叶变换。例如,如果 X 是矩阵,则 fft(X,n,2) 返回每行的 n 点傅里叶变换。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方,但是这里直接取读取出来的样本数作为N。
FFT 计算公式如下:
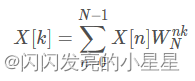
Xk 长度与 N 相同。
根据奈科斯特定律,只有 f=fs/2 范围内的信号才是被采样到的有效信号,因此得到的频谱肯定是关于 N/2 对称的(就是只看前一半的波形就好)。
第k点的实际频率的计算为 f(k) = k * (fs / n) — — (横轴的频率范围为 :f = n * fs / N;)
X[0] 为直流分量 ,幅值 = 模值(X[0]) / N
X[k] 为个点的频率分量(除X[0]外),幅值 = 模值(X[k]) / (N / 2)
示例
使用傅里叶变换求噪声中隐藏的信号的频率分量。
指定信号的参数,采样频率为 1 kHz,信号持续时间为 1.5 秒。
Fs = 1000; % Sampling frequency
T = 1/Fs; % Sampling period
L = 1500; % Length of signal
t = (0:L-1)*T; % Time vector
构造一个信号,其中包含幅值为 0.7 的 50 Hz 正弦量和幅值为 1 的 120 Hz 正弦量。
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
用均值为零、方差为 4 的白噪声扰乱该信号。
X = S + 2*randn(size(t));
在时域中绘制含噪信号。通过查看信号 X(t) 很难确定频率分量。
plot(1000*t(1:50),X(1:50))
title("Signal Corrupted with Zero-Mean Random Noise")
xlabel("t (milliseconds)")
ylabel("X(t)")

计算信号的傅里叶变换。
Y = fft(X);
计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
定义频域 f 并绘制单侧幅值频谱 P1。与预期相符,由于增加了噪声,幅值并不精确等于 0.7 和 1。一般情况下,较长的信号会产生更好的频率逼近值。
f = Fs*(0:(L/2))/L;
plot(f,P1)
title("Single-Sided Amplitude Spectrum of X(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")
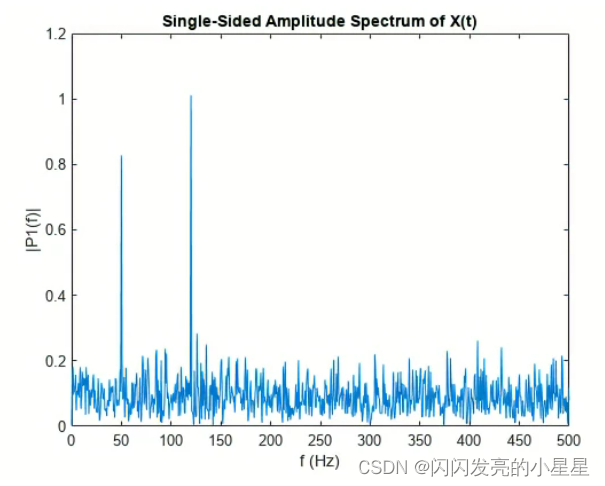
现在,采用原始的、未破坏信号的傅里叶变换并检索精确幅值 0.7 和 1.0。
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
plot(f,P1)
title("Single-Sided Amplitude Spectrum of S(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")
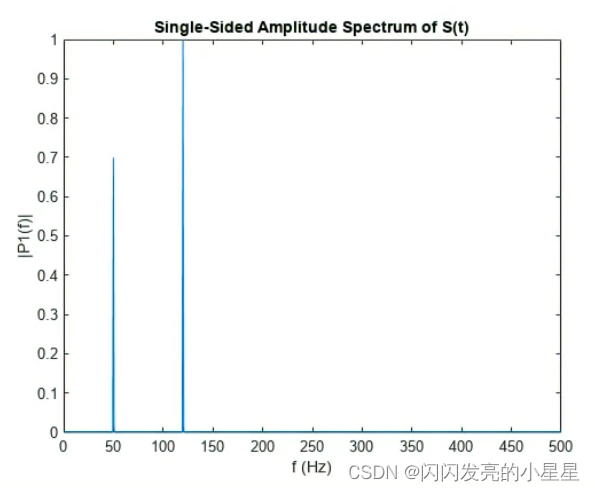
问题
其他参考:
Matlab 计算 FFT 的方法及幅值问题
matlab 官网:快速傅里叶变换