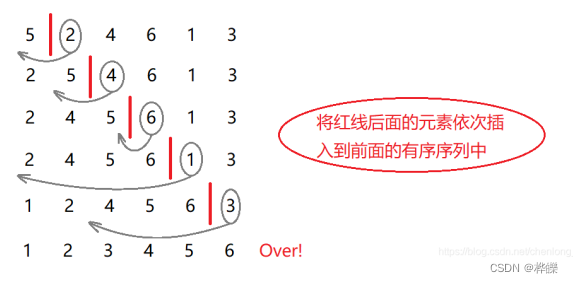
简单选择排序

#include<iostream>
using namespace std;

#define MAXSIZE 20  //记录最大个数
typedef int KeyType;  //关键字类型

typedef int InfoType;

//定义每个记录（数据元素）的结构
struct RecType
    //Record Type：每条记录的类型
{
    KeyType key;  //关键字
    InfoType otherinfo;  //其他数据项
};

struct SqList
    //顺序表(的)结构
{
    RecType r[MAXSIZE + 1];
    //类型为【记录类型】的数组
    //r[0]一般做哨兵或缓冲区
    int length;  //顺序表长度
};

void SelectSort(SqList& L)
{
    for (int i = 1; i <= L.length; i++)
    {
        int k = L.r[i].key;
        for (int j = i; j <= L.length; j++)
        {
            if (L.r[j].key < k)
                k = L.r[j].key;
        }
        if (k != L.r[i].key)
        {
            int temp = L.r[i].key;
            L.r[i].key = k;
            k = temp;
        }
    }
}


int main()
{

}

堆排序

堆的调整：

大根堆

void HeapAdjust(Elem R[], int s, int m) //Heap：堆
//二叉树空间范围：s-m，这里写的是大根堆
// s：smallest
// m：max
{
    //调整R[s]的关键字，使R[s...m]重新成为一个大根堆
    Elem rc = R[s];
    for (int j = 2 * s; j <= m; j *= 2)
    {
        if (j < m && R[j] < R[j + 1])
            j++;  //j为关键字较大的数据元素下标
        if (rc >= R[j])
            break;
        R[s] = R[j];
        s = j;  //记录位置
    }
    R[s] = rc;  //插入
}

在一开始（最开始），我们看这个程序，那是根本完全看不懂，艹

我们甚至还提出了问题：他这里是怎么找到最后一个元素的？？？我怎么没看出来呀

于是就先依葫芦画瓢先造出/想办法搞出一个小根堆来试试：

小根堆

void HeapAdjust(Elem R[], int s, int m) //小根堆
{
    Elem rc = R[s];
    for (int j = 2 * s; j <= m; j *= 2)
    {
        if (j < m && R[j] > R[j + 1])
            j++;  //j为关键字较小的数据元素下标
        if (rc <= R[j])
            break;
        R[s] = R[j];
        s = j;  //记录位置
    }
    R[s] = rc;  //插入
}

然后我们对着程序沉默死磕半天，终于咂摸着知道这东西写的是啥玩意了：

整个堆调整的完整工序如下：

而这里（实际上我们这里）：

PPT实际上写的其实是步骤二（图2）到步骤四（图4）这个整个过程的算法

而不是tmd从图1开始的整个过程的算法

程序开始时他已经默认完前面从图1到图2的过程操作已经给我们提前安排操作好了

TMD!

根据按照操作对程序注解标注：（看过了注解就知道程序他每一步是怎么操作的了）

以小根堆为例：（大根堆同理，这里就不再赘述）

void HeapAdjust(Elem R[], int s, int m) //小根堆
{
    Elem rc = R[s];
    //此时最后的元素已经被放到堆顶，rc记录最后一位元素
    for (int j = 2 * s; j <= m; j *= 2)
        //从第二层子树开始遍历
    {
        if (j < m && R[j] > R[j + 1])
            j++; 
        //j：关键字较小的元素下标
        if (rc <= R[j])
            break;
        //要最后一个元素比他小就算了，不然的话：
        R[s] = R[j];
        //j（较小）元素放上面去
        s = j;  
        //下一轮for循环：
        //从上一轮j的位置开始往下遍历
        //以j的位置为根，向下遍历子树，不断把值小的元素移上去
    }
    R[s] = rc; 
    //最后，把最后的元素插入到最底部
    // 注：
    // 最后退出循环的时候s已经指向最底层了
    // 而不出意外的话，最后的元素理论上也应该是堆里面最大的一个元素
}

堆的建立

#include<iostream>
using namespace std;

typedef int Elem;

void HeapAdjust(Elem R[], int s, int m) //小根堆
{
    Elem rc = R[s];
    //此时最后的元素已经被放到堆顶，rc记录最后一位元素
    for (int j = 2 * s; j <= m; j *= 2)
        //从第二层子树开始遍历
    {
        if (j < m && R[j] > R[j + 1])
            j++; 
        //j：关键字较小的元素下标
        if (rc <= R[j])
            break;
        //要最后一个元素比他小就算了，不然的话：
        R[s] = R[j];
        //j（较小）元素放上面去
        s = j;  
        //下一轮for循环：
        //从上一轮j的位置开始往下遍历
        //以j的位置为根，向下遍历子树，不断把值小的元素移上去
    }
    R[s] = rc; 
    //最后，把最后的元素插入到最底部
    // 注：
    // 最后退出循环的时候s已经指向最底层了
    // 而不出意外的话，最后的元素理论上也应该是堆里面最大的一个元素
}

void Swap(int a, int b)
{
    int temp=b;
    b = a;
    a = temp;
}

void HeapSort(Elem R[],int n)
{
    int i;
    for (i = n / 2; i >= 1; i--)  
        HeapAdjust(R, i, n);
    // 我们默认R[]数据无序
    // 先把R[]中的无序数据都排一遍顺序
    // 相当于我们先构造出一个合格的图1

    for (i = n; i > 1; i--)
    {
        cout << R[1] << endl;//逐个输出元素
        Swap(R[1], R[i]);  
        //互换最后一个元素和根
        //相当于执行图1加工到图2的过程

        HeapAdjust(R, 1, i - 1); 
        //面向剩下的元素重新建堆
    }
}

int main()
{

}