目录
供水管线
黑客小码哥
逆序
来给单词分类
前k小数(进阶)
前K小数
线段树
队列安排
一元多项式的加法
快排变形
供水管线
难度:钻石
0时间限制:1秒
巴占用内存:128M
在个城市之间原本要规划修建许多条下水管道,管理人员发现这些管道会形成一条
回路,而下水道只要将城市联通即可,所以回路会加大施工的成本。所以希望你来帮忙
找出多余的管道来进行优化。当然管道和管道之间是有区别的,比如用s来表示i到
的管道管理费用,S越小则表示该管道管理费用越低。能否去除一些管线,使得总
管理成本最低。求出最低的管理成本(不存在自身与自身成为回路的管道)。

//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e2 + 7;
struct NODE{
int i,j,c;
bool operator<(const NODE &t)const { return c < t.c;}
}p[N];
int fa[N],n,k,ans;
void init(){
for (int i=1;i<N;i++)
fa[i]= i;
}
int find(int x){return x == fa[x] ? x: (fa[x] = find(fa[x]));}
void mer(int x,int y) {
x = find(x), y = find(y);
if (x != y)
fa[x] = y;
}
int main(){
init();
cin >>n >> k;
for (int i=1;i<=k;i++)
cin >> p[i].i>>p[i].j>>p[i].c;
sort(p + 1,p + 1 + k);
for (int i=1;i<=k;i++)
if (find(p[i].i)!=find(p[i].j)){
ans += p[i].c;
mer(p[i].i,p[i].j);
}
cout <<ans;
return 0;
}
黑客小码哥
难度:黄金
时间限制:1秒
巴占用内存:256M
小码哥是一名黑客,他最近刚彩票中奖,由于还没兑换,小码哥十分担心彩票被盗(小
码哥过分谨慎了),他想为自己的保险箱设新的密码,顺便他想让你测试编码。
现有两种编码方式:
1.对于己知字符串中的某种字符,全部变成另一种字符。如里面出现的A全部换成B;
2.对于当前字符串,打乱字符顺序。
先给你一个加密后的字符串和加密前的字符串,判断加密前的字符串是否能得到加密后
的字符串。字符串中字符均为大写字母。
格式
输入格式:第一行加密后的字符串;
第二行加密前的字符串;
有多组数据输入。
/*
MT2128 黑客小码哥
*/
#include<bits/stdc++.h>
using namespace std;
const int LETERCNT = 26;
// 判断两个字符串是否有可能是经过指定加密算法处理前后的两串
bool isSamePossiblely(string str1, string str2){
// 长度不同就一定不是
int strlen = str1.length();
if(strlen != str2.length()) return false;
// 否则进一步判断各字符的出现次数是否一致
int ary1[LETERCNT]={0}, ary2[LETERCNT]={0};
// 先统计各字符串中不同字符的出现次数(即认为存在字符变换操作)
for(int i=0; i<strlen; i++){
ary1[str1[i]-'A']++;
ary2[str2[i]-'A']++;
}
// 消除字符间的顺序差异(即认为存在字符顺序变换操作)
sort(ary1, ary1+LETERCNT);
sort(ary2, ary2+LETERCNT);
// 判断是否可能是变换前后的两字符串
for(int i=0;i<LETERCNT;i++)
if(ary1[i] != ary2[i])
return false;
return true;
}
int main()
{
string str1, str2;
while(cin>>str1>>str2) {
if(isSamePossiblely(str1, str2)) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int st1[30],st2[30];
int main(){
while (cin >>s1 >>s2){
memset(st1,0,sizeof(st1));
memset(st2,0,sizeof(st2));
if (s1.length()!=s2.length()){
cout <<"NO"<<endl;
continue;
}
for (int i=0;i<s1.length();i++)
st1[s1[i]-'A']++,st2[s2[i]-'A']++;
sort(st1,st1 +26);
sort(st2,st2 + 26);
bool flag = true;
for (int i=0;i<26;i++){
if (st1[i] != st2[i]){
cout <<"NO"<<endl;
flag = false;
break;
}
}
if (flag)
cout <<"YES"<<endl;
}
return 0;
}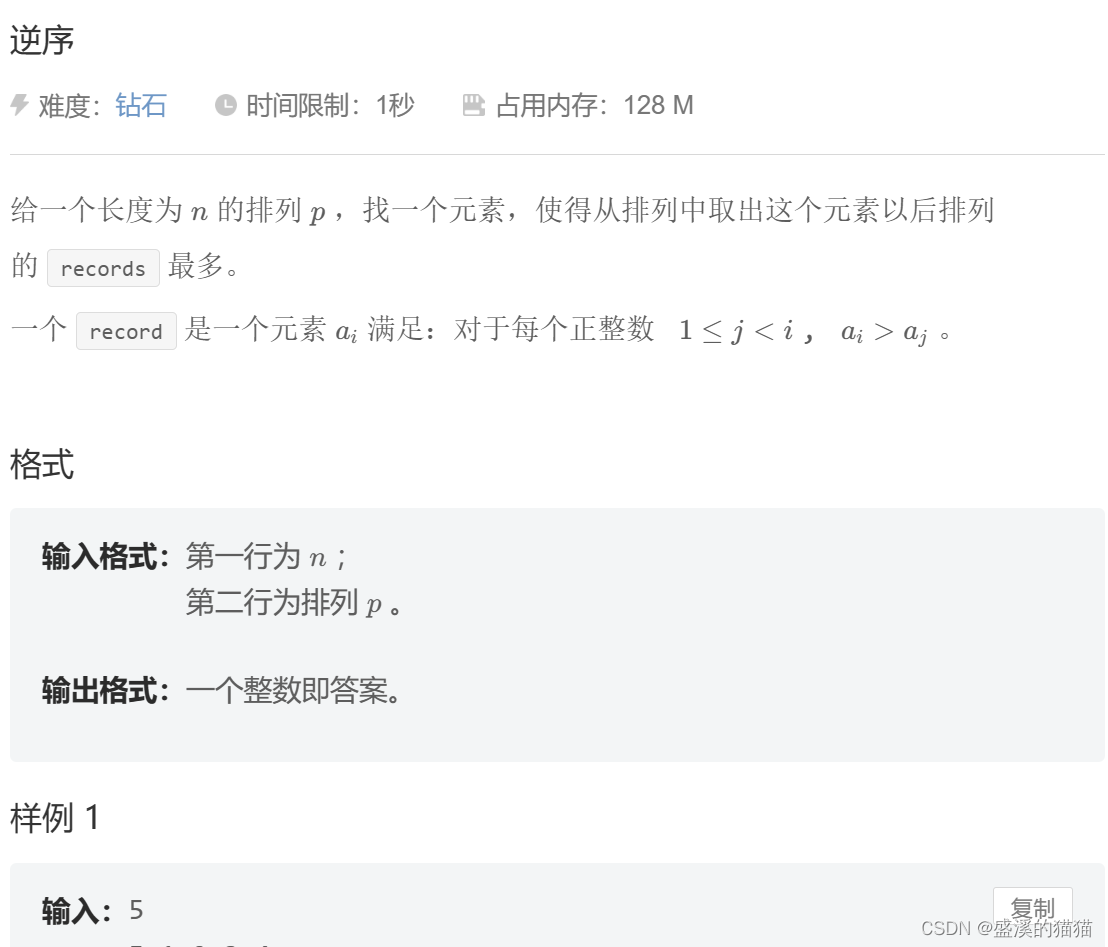
逆序
号难度:钻石
0时间限制:1秒
巴占用内存:128M
给一个长度为的排列p,找一个元素,使得从排列中取出这个元素以后排列
的
records
最多。
一个
record
是一个元素a,满足:对于每个正整数1≤j<i,a>aj。
格式
输入格式:第一行为n;
第二行为排列p。
输出格式:一个整数即答案。
样例1
输入:5
复制
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
const int N=1e5 + 7;
int n;
int c[N],chg [N];
int lowbit(int x){return x & -x;}
void add(int x){
for (;x < N;x += lowbit(x))
c[x]++;
}
int sum(int x){
int ret =0;
for (;x> 0;x -= lowbit(x))
ret += c[x];
return ret;
}
int main(){
cin >> n;
int x=0,maxx =0;
for (int i=1;i<=n;i++){
cin >>x;
maxx = max(maxx,x);
int cnt = sum(x);
if (cnt ==i-1)
chg [maxx]--;
else if (cnt ==i-2)
chg [maxx]++;
add (x);
}
int ans = 1;
for (int i = 1;i <= n;i++)
if (chg[i] > chg[ans])
ans = i;
cout <<ans <<endl;
return 0;
}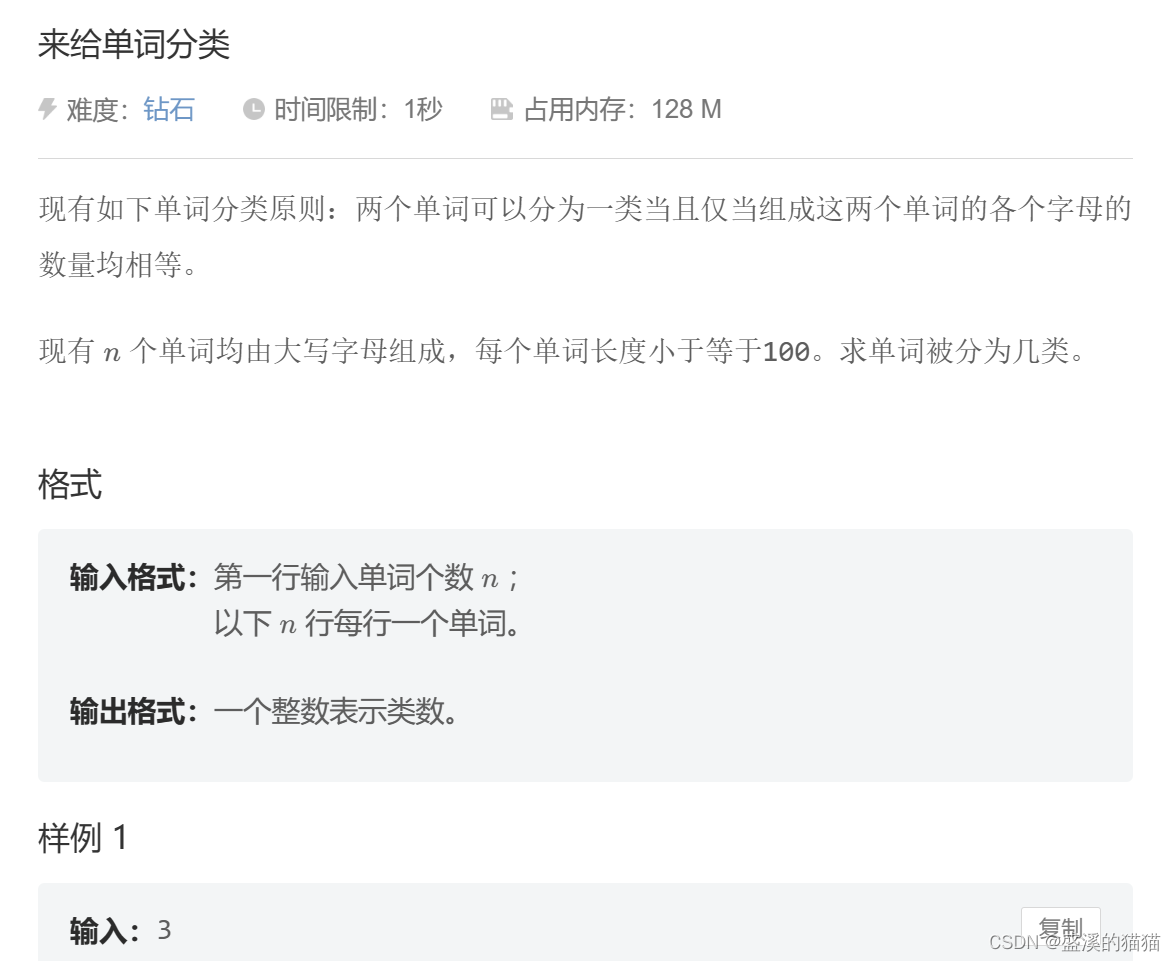
来给单词分类
难度:钻石
0时间限制:1秒
巴占用内存:128M
现有如下单词分类原则:两个单词可以分为一类当且仅当组成这两个单词的各个字母的
数量均相等。
现有n个单词均由大写字母组成,每个单词长度小于等于10。求单词被分为几类。
格式
输入格式:第一行输入单词个数n;
以下n行每行一个单词。
输出格式:一个整数表示类数。
样例1
输入:3
复制
import java.util.Scanner;
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int n= Integer.parseInt(input.next());
Set<String> a=new HashSet<>();
for (int i = 0; i < n; i++) {
char[] ch=input.next().toCharArray();
int[] b=new int[26];
for (int j = 0; j < ch.length; j++) {
b[ch[j]-'A']++;
}
a.add(Arrays.toString(b));
}
System.out.println(a.size());
input.close();
}
}
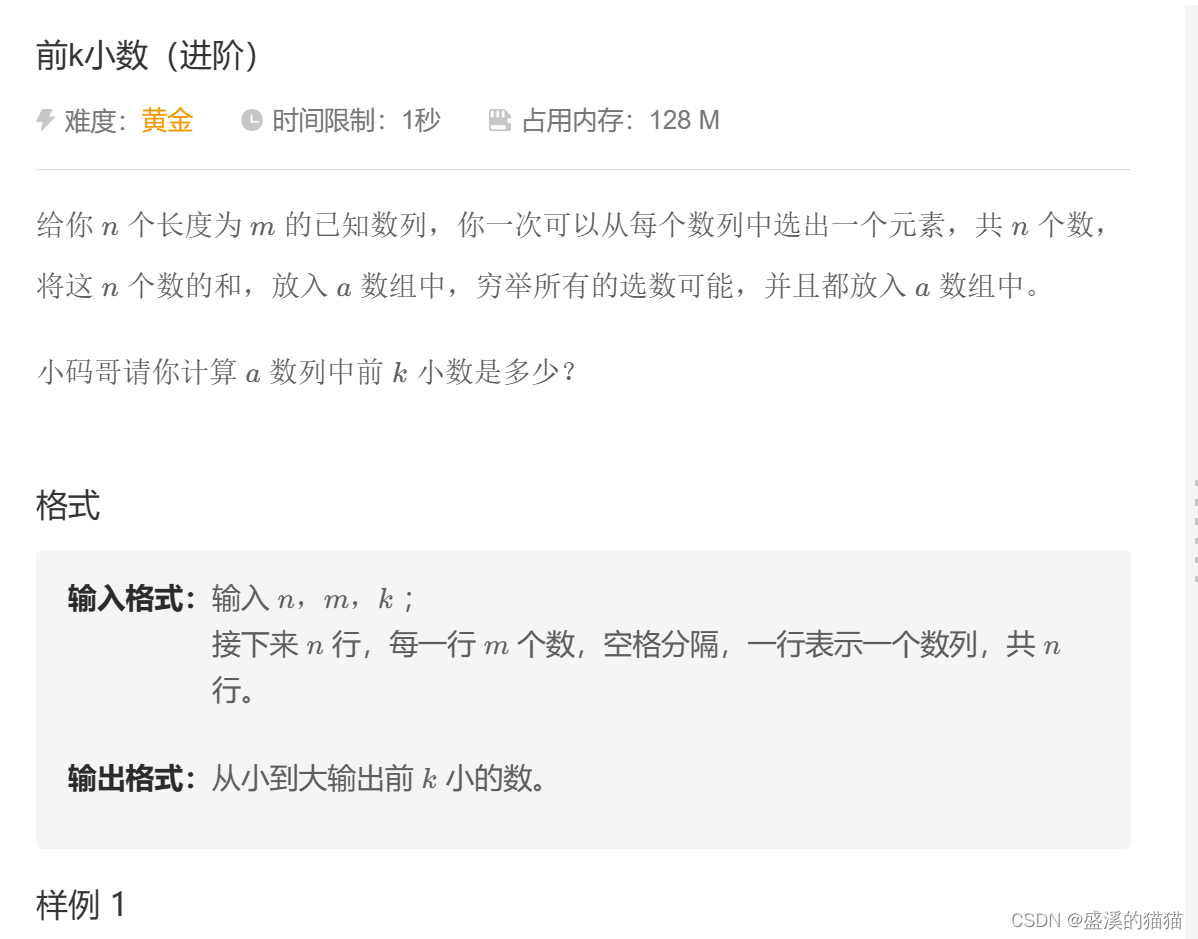
前k小数(进阶)
难度:黄金
时间限制:1秒
巴占用内存:128M
给你n个长度为m的已知数列,你一次可以从每个数列中选出一个元素,共n个数,
将这n个数的和,放入a数组中,穷举所有的选数可能,并且都放入a数组中。
小码哥请你计算a数列中前k小数是多少?
格式
输入格式:输入n,m,k;
接下来n行,每一行m个数,空格分隔,一行表示一个数列,共n
行。
输出格式:从小到大输出前k小的数。
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 + 7;
int n,m,k,a[N],b[N],c[N];
struct NODE {
int ida, idb, num;
bool operator>(const NODE &a) const { return num > a.num; }
}tmp;
priority_queue<NODE,vector<NODE>,greater<NODE>>q;
int main(){
cin>>n>>m>>k;
for (int i=1;i <=m;i++)
cin >>a[i];
for (int i = 1;i<=m;i++)
cin >>b[i];
sort(a + 1,a + m + 1);
sort(b+1,b+m+1);
for (int i = 1;i<=m;i++)
q.push({i,1,a[i]+b[1]});
for (int i = 1;i<=k;i++) {
tmp = q.top(), q.pop();
c[i] = tmp.num;
tmp.num = a[tmp.ida] + b[++tmp.idb];
q.push(tmp);
}
n-=2;
while (n--){
while (!q.empty())
q.pop();
for (int i=1;i <= k;i++)
a[i]=c[i];
for (int i=1;i <=m;i++)
cin >>b[i];
sort(b+1,b+m+1);
for (int i=1;i <=k;i++)
q.push({i,1,a[i]+b[1]});
for (int i=1;i <=k;i++) {
tmp = q.top(), q.pop();
c[i] = tmp.num;
tmp.num = a[tmp.ida] + b[++tmp.idb];
q.push(tmp);
}
}
for (int i=1;i<=k;i++)
cout <<c[i]<<" ";
return 0;
}
前K小数
难度:黄金
©时间限制:1秒
巴占用内存:128M
小码哥现在手上有两个长度为n的数列a,b,(1≤i,j≤n)通过a,+b,可以构造
出n*n个数,求构造出的数中前k小的数。
格式
输入格式:第一行2个数n,k;
第二行n个数,表示数列a;
第三行n个数,表示数列b。
输出格式:从小到大输出前飞小的数。
样例1
输入:33
复制
266
#include<bits/stdc++.h>
using namespace std;
const int maxSize = 10100;
int a[maxSize];
int b[maxSize];
struct Node{
int sum,b;
Node(int sum,int b):sum(sum),b(b){}
bool operator < (const Node &b) const{
return sum>b.sum;
}
};
priority_queue<Node>minList;
int main(){
int n,k;
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
}
for(int i=0;i<n;i++){
cin>>b[i];
}
sort(a,a+n);
sort(b,b+n);
for(int i=0;i<n;i++){
minList.push(Node(a[i]+b[0],0));
}
for(int i=0;i<k;i++){
Node node=minList.top();
minList.pop();
cout<<node.sum<<" ";
int tempB = node.b;
if(tempB+1<n){
minList.push(Node(node.sum-b[tempB]+b[tempB+1],tempB+1));
}
}
return 0;
}

线段树
难度:钻石
0时间限制:1秒
巴占用内存:128M
线段树模板题。已知一个数列,你需要进行下面两种操作:将某区间每一个数加上
,求出某区间每一个数的和。
格式
输入格式:第一行包含两个整数n,m(5≤n,m≤105),分别表示该数列数字的
个数和操作的总个数;
第二行包含n个用空格分隔的整数(0-109),其中第i个数字表
示数列第i项的初始值:
接下来行每行包含3或4个整数,表示一个操作,具体如下:
1xyk:将区间[X,y]内每个数加上k。
2xy:输出区间[x,y内的数的和。
其中:1≤x≤y≤n,0≤k≤105。
输出格式:输出包含若干行整数,
即为所有操作2的结果。
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
const int N=1e5 + 7;
#define int long long//有时候觉得ll麻烦,就可以用。但记得改signed main
struct NODE {
int l, r, val, lz;//lz为懒标记
}tree[4 * N];
int a[N];
void build(int p,int l,int r){
tree[p].l=l,tree[p].r=r;
if(l==r){
tree[p].val = a[l];
return;
}
int mid =l + ((r-l)>>1);
build(p *2,l,mid);
build(p *2 + 1,mid + 1,r);
tree[p].val = tree[p* 2].val + tree[p * 2+ 1].val;
}
void lazy(int p,int v) {
int s = tree[p].l, t = tree[p].r;
tree[p].val += (t - s + 1) * v, tree[p].lz += v;
}
void pushdown(int p){
lazy(2 * p,tree[p].lz);
lazy(2 * p +1,tree[p].lz);
tree[p].lz = 0;
}
//带懒标记区间修改,[1,r]
//为修改区间,p为当前节点编号,c为区间节点变化值,求和非求最值
void update(int l,int r,int c,int p){
int s =tree[p].l,t = tree[p].r;
if (l <=s && t <=r)
return lazy(p,c);
if (tree[p].lz && s != t)
pushdown(p);
int mid = s +((t -s)>>1);
if (l<=mid)
update(l,r,c,p * 2);
if (r > mid)
update(l,r,c,p * 2+1);
tree[p].val =tree[p * 2].val+ tree[p * 2 + 1].val;
}
//带懒标记区间查询(区间求和),[L,r】为修改区间,p为当前节点编号
int query(int l,int r,int p) {
int s = tree[p].l, t = tree[p].r;
if (l <= s && t <= r)
return tree[p].val;
if (tree[p].lz)
pushdown(p);
int mid = s + ((t - s) >> 1), sum = 0;
if (l <= mid)
sum = query(l, r, p * 2);
if (r > mid)
sum += query(l, r, p * 2 + 1);
return sum;
}
signed main(){
int n,m;
cin>>n>>m;
for (int i=1;i<=n;i++)
cin >>a[i];
build(1,1,n);
while (m--){
int op,x,y,k;
cin >>op;
if (op ==1) {
cin >> x >> y >> k;
update(x, y, k, 1);
}else{
cin >>x >>y;
cout <<query(x,y,1)<<endl;
}
}
return 0;
}
队列安排
难度:黄金
时间限制:1秒
巴占用内存:128M
一个学校里老师要将班上N个同学排成一列,同学被编号为1~N,他采取如下的方
法:
1.先将1号同学安排进队列,这时队列中只有他一个人:
2.2一N号同学依次入列,编号为1的同学入列方式为:老师指定编号为1的同学站在
编号为1~(亿一1)中某位同学(即之前已经入列的同学)的左边或右边:
3.从队列中去掉M(M<N)个同学,其他同学位置顺序不变。
在所有同学按照上述方法队列排列完毕后,老师想知道从左到右所有同学的编号。
格式
输入格式:第1行为一个正整数N,表示了有N个同学;
第2一N行,第i行包含两个整数k,p,其中k为小于i的正整数,
p为0或者1。若p为0,则表示将i号同学插入到k号同学的左边,p
为1耒示活入右力·
#include<iostream>
#include<bits/stdc++.h>
#include<algorithm>
#include<math.h>
#include<string.h>
#include<string>
using namespace std;
const int N = 1e6+10;
struct line
{
int pr, ne;
bool mk;
}a[N];
int f[N];
int n , m;
int ans = 0;
int main()
{
cin >> n;
int i , j;
int k , p;
a[0].ne = 1;
a[0].pr = 0;
a[1].mk = 1;
a[1].pr = 0;
for(i = 2 ; i <= n ; i++)
{
cin >> k >> p;
a[i].mk = 1;
if(p == 0)
{
a[a[k].pr].ne = i;
a[i].pr = a[k].pr;
a[k].pr = i;
a[i].ne = k;
}
else
{
a[a[k].ne].pr = i;
a[i].pr = k;
a[i].ne = a[k].ne;
a[k].ne = i;
}
}
cin >> m;
int x;
for(i = 1 ; i <= m ; i++)
{
cin >> x;
if(!a[x].mk)
{
continue;
}
a[x].mk = 0;
a[a[x].pr].ne = a[x].ne;
a[a[x].ne].pr = a[x].pr;
}
printf("%d",a[0].ne);
int now = a[0].ne;
now = a[now].ne;
while(now)
{
printf(" %d",now);
now = a[now].ne;
}
cout << endl;
return 0;
}

一元多项式的加法
号难度:钻石
0时间限制:1秒
巴占用内存:128M
小码哥给出两个一元多项式工4和工B,请你将这两个一元多项式相加,得到新的一元
多项式Lc。
如样例:
L4=1-10x6+2x8+7x14
LB=-x4+10x6-3x19+8x14+4x18
LC=LA+LB=1-x4+2x8-3x19+15x14+4x18
格式
输入格式:第一行两个整数n和m,分别表示L4和LB的项数;
接下来n行,每行输入工4的每一项的信息,两个整数分别表示该项
的系数coef和次数expm,输入保证次数递增;
接下来m行,每行输入LB的每一项的信息,两个整数分别表示该项
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N =2e6 +7;
struct NODE {
ll nex, coef, expn;
}node [N];
int n,m,head,tail,pos;
ll coefA[N],expnA[N],coefB[N],expnB[N];
void insert(int curr,ll val1,ll val2){
node[++pos].coef = val1;
node[pos].expn = val2;
node[pos].nex = node[curr].nex;
node[curr].nex = pos;
if (!node[pos].nex)
tail = pos;
}
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf("%ld%lld",&coefA[i],&expnA[i]);
for (int i=1;i<=m;i++)
scanf("%lld%lld",&coefB[i],&expnB[i]);
int l=1,r=1;
while (l <=n &&r<=m) {
if (expnA[l] == expnB[r]) {
insert(tail, coefA[l] + coefB[r], expnA[l]);
l++, r++;
} else {
if (expnA[l] < expnB[r]) {
insert(tail, coefA[l], expnA[l]);
l++;
} else {
insert(tail, coefB[r], expnB[r]);
r++;
}
}
}
while (l <=n) {
insert(tail, coefA[l], expnA[l]);
l++;
}
while (r <=m) {
insert(tail, coefB[r], expnB[r]);
r++;
}
for (int i=node[head].nex;i!=0;i=node[i].nex)
if (node[i].coef !=0)
printf("%lld %lld\n",node[i].coef,node[i].expn);
return 0;
}
快排变形
难度:黄金
0时间限制:1秒
巴占用内存:128M
有”个数,问如果通过每次交换邻项的两个数来使数组中的元素变为升序排列。
eg:98765,
变为升序:
56789.
需要10次邻项交换。
格式
输入格式:第一行输入一个整数n,表示序列长度:
第二行输入n个数。
输出格式:输出一个整数,表示最少的交换次数。
//
// Created by abner on 2023/5/10.
//
#include <bits/stdc++.h>
using namespace std;
const int N=2e5 +7;
int a[N],b[N],c[N],n;
long long ans;
int lowbit(int x){return x &-x;}
void add(int i,int x){
for (;i<=n;i+=lowbit(i))
c[i]+=x;
}
int sum(int i){
int ans =0;
for (;i>0;i-=lowbit(i))
ans +=c[i];
return ans;
}
bool cmp(const int x,const int y){
if (b[x]==b[y])
return x >y;
return b[x] > b[y];
}
int main(){
cin >>n;
for (int i=1;i<=n;i++) {
cin >> b[i];
a[i] = i;
}
sort(a +1,a +n+1,cmp);
for (int i=1;i<=n;i++){
add(a[i],1);
ans += sum(a[i]-1);
}
cout <<ans <<endl;
return 0;
}







![[Java基础练习-002]综合应用(基础进阶),如果你会做,那说明你java入门了,](https://img-blog.csdnimg.cn/ea68ec2aa1874ef3b06fdc00d81c5960.png)