20230503 - 二叉树2 | 二叉树的层序遍历、226. 翻转二叉树、101. 对称二叉树

1、二叉树的层序遍历

二叉树的层序遍历，就是图论中的广度优先搜索在二叉树中的应用，需要借助队列来实现（此时又发现队列的一个应用了）。

来吧，一口气打十个：

102.二叉树的层序遍历

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        //队列存储，进行层序遍历
        Queue<TreeNode> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        while(!q.isEmpty()){
            //记录每一行的
            ArrayList<Integer> row = new ArrayList<>();
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                TreeNode cur = q.poll();
                row.add(cur.val);
                //若是左右孩子存在，则存入左右孩子作为下一次层次
                if(cur.left!=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            } 
            //每一层加入输出
            res.add(row);
        }
        return res;
    }
}

107.二叉树的层次遍历II

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        //队列存储，进行层序遍历
        Queue<TreeNode> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        while(!q.isEmpty()){
            //记录每一行的
            ArrayList<Integer> row = new ArrayList<>();
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                TreeNode cur = q.poll();
                row.add(cur.val);
                //若是左右孩子存在，则存入左右孩子作为下一次层次
                if(cur.left!=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            } 
            //每一层加入输出
            res.add(row);
        }
        List<List<Integer>> res1 = new ArrayList<>();
        for(int i=res.size()-1;i>=0;i--){
            res1.add(res.get(i));
        }
        return res1;
    }
}

199.二叉树的右视图

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        // List<List<Integer>> res = new ArrayList<>();
          List<Integer> list = new ArrayList<>();
        if(root == null) return list;
        //队列存储，进行层序遍历
        Queue<TreeNode> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        while(!q.isEmpty()){
            //记录每一行的
            ArrayList<Integer> row = new ArrayList<>();
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                TreeNode cur = q.poll();
                row.add(cur.val);
                //若是左右孩子存在，则存入左右孩子作为下一次层次
                if(cur.left!=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            } 
            //每一层加入输出
            list.add(row.get(row.size()-1));
        }

       
        return list;
    }
}

637.二叉树的层平均值

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> list = new ArrayList<>();
        if(root == null) return list;
        //队列存储，进行层序遍历
        Queue<TreeNode> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        
        while(!q.isEmpty()){
            //记录每一行的
             double levelSum = 0.0;
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                TreeNode cur = q.poll();
                levelSum += cur.val;
                //若是左右孩子存在，则存入左右孩子作为下一次层次
                if(cur.left!=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            } 
            //每一层加入输出
            list.add(levelSum / n);
        }

        return list;
    }
}

429.N叉树的层序遍历

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
          List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        //队列存储，进行层序遍历
        Queue<Node> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        while(!q.isEmpty()){
            //记录每一行的
            ArrayList<Integer> row = new ArrayList<>();
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                Node cur = q.poll();
                row.add(cur.val);
                // //若是左右孩子存在，则存入左右孩子作为下一次层次
                // if(cur.left!=null) q.add(cur.left);
                // if(cur.right !=null) q.add(cur.right);
                List<Node> children = cur.children;
                if(children == null || children.size()==0) continue;
                for(Node child:children){
                    if(child!=null) q.add(child);
                }
            } 
            //每一层加入输出
            res.add(row);
        }
        return res;
    }
}

515.在每个树行中找最大值

class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;
        Queue<TreeNode> q = new ArrayDeque<>();
        q.add(root);
        while(!q.isEmpty()){
            //记录最大值
            int maxVal = Integer.MIN_VALUE;
            int len = q.size();
            for(int i=0;i<len;i++){
                //当前访问节点
                TreeNode cur = q.poll();
                if(maxVal<cur.val) maxVal = cur.val;
                //左右子树不为空进行记录
                if(cur.left!=null) q.add(cur.left);
                if(cur.right!=null) q.add(cur.right);
            }

            //结束时记录
            res.add(maxVal);
        }
        return res;
    }
}

116.填充每个节点的下一个右侧节点指针、
117.填充每个节点的下一个右侧节点指针II

class Solution {
    public Node connect(Node root) {
        if(root == null) return root;
        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while(!q.isEmpty()){
            int len =q.size();
            for(int i=0;i<len;i++){
                //当前节点
                Node cur = q.poll();
                //指向next
                if(i< len-1){
                    cur.next = q.peek() ;//出了队列，因此peek指向的就是下一个元素
                }
                //把node的左右孩子加入
                if(cur.left!=null) q.add(cur.left);
                if(cur.right!=null) q.add(cur.right);
            }
        }
        return root;
    }
}

104.二叉树的最大深度

class Solution {
    public int maxDepth(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return 0;
        //队列存储，进行层序遍历
        Queue<TreeNode> q = new ArrayDeque<>();
        //第一个入队
        q.add(root);
        while(!q.isEmpty()){
            //记录每一行的
            ArrayList<Integer> row = new ArrayList<>();
            int n = q.size();
            //因为先进入的是根节点，故每层节点多少，队列大小就是i多少
            for(int i=0;i<n;i++){
                //接收临时
                TreeNode cur = q.poll();
                row.add(cur.val);
                //若是左右孩子存在，则存入左右孩子作为下一次层次
                if(cur.left!=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            } 
            //每一层加入输出
            res.add(row);
        }
        return res.size();
    }
}
、

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null)   return 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        int depth = 0;
        while (!que.isEmpty())
        {
            int len = que.size();
            while (len > 0)
            {
                TreeNode node = que.poll();
                if (node.left != null)  que.offer(node.left);
                if (node.right != null) que.offer(node.right);
                len--;
            }
            depth++;
        }
        return depth;
    }
}

111.二叉树的最小深度

class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        Queue<TreeNode> q = new LinkedList<>();
        q.add(root);
        int depth = 0;
        while(!q.isEmpty()){
            int len = q.size();
            depth++;
            for(int i=0;i<len;i++){
                TreeNode cur  = q.poll();
                //如果当前节点的左右子树都为空，说明就是最小高度
                if(cur.left == null && cur.right == null) return depth;
                if(cur.left !=null) q.add(cur.left);
                if(cur.right !=null) q.add(cur.right);
            }
        }

        return depth;
    }
}

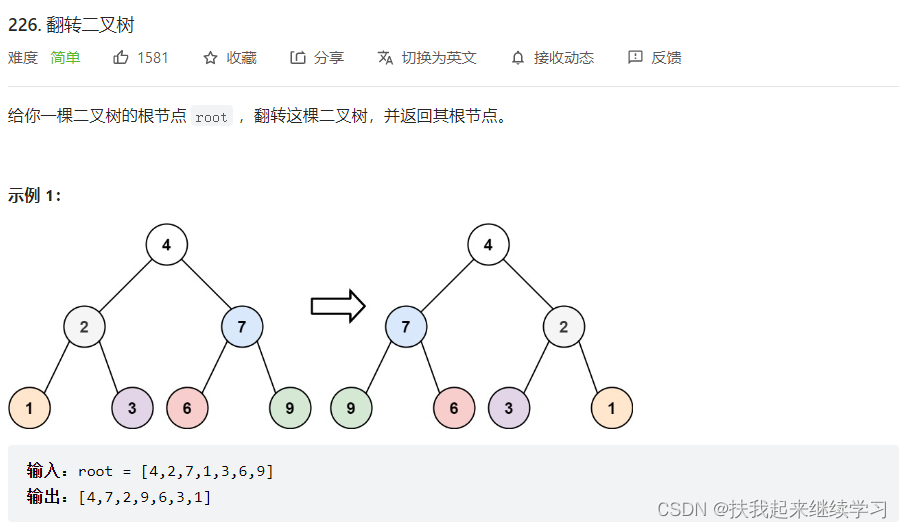
2、226. 翻转二叉树

在这里插入图片描述

DFS

class Solution {
    public TreeNode invertTree(TreeNode root) {
        //使用前序遍历
        if(root == null) return null;
        //前
        swap(root);
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
    public void swap(TreeNode node){
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
    }
}

BFS

class Solution {
    public TreeNode invertTree(TreeNode root) {
        //使用前序遍历
        // if(root == null) return null;
        // //前
        // swap(root);
        // invertTree(root.left);
        // invertTree(root.right);
        // return root;
        if(root == null) return null;
        //层序遍历
        Queue<TreeNode> q = new LinkedList<>();
        q.add(root);

        while(!q.isEmpty()){
            int len = q.size();
            for(int i=0;i<len;i++){
                TreeNode cur = q.poll();
                swap(cur);
                if(cur.left!=null) q.add(cur.left);
                if(cur.right!=null) q.add(cur.right);
            }
        }

        return root;

    }
    public void swap(TreeNode node){
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
    }
}

3、101. 对称二叉树

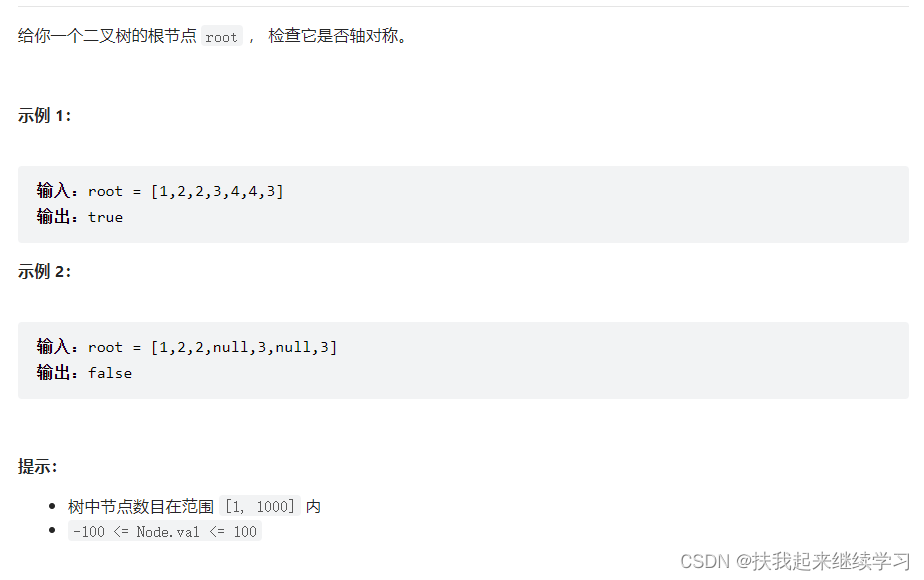
在这里插入图片描述
左节点为空，右节点不为空，不对称，return false
左不为空，右为空，不对称 return false
左右都为空，对称，返回true
此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

左右都不为空，比较节点数值，不相同就return false
此时左右节点不为空，且数值也不相同的情况我们也处理了。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left,root.right);

    }

    public boolean compare(TreeNode left,TreeNode right){
        //左节点为空，右节点不为空，不对称，return false
        if(left == null && right !=null) return false;
        //左节点不为空，右节点为空，不对称
        if(left!=null && right == null) return false;
        //左右节点都为空，说明对称
        if(left==null && right == null) return true;

        //左节点不等于右节点
        if(left.val !=right.val){
            return false;
        }

        //比较外侧
        boolean c = compare(left.left,right.right);

        //比较内测
        boolean d = compare(left.right,right.left);

        return c&&d;
    }
}