硬件通信之 从单片机到C/C++指针详解

news2024/10/7 8:23:33

 一  单片机理论概述

1.1 单片微型计算机（Single Chip Microcomputer）简称单片机，是把组成微型计算机的主要功能部件（CPU、RAM、ROM、I/O口、定时/计数器、串行口等）集成在一块芯片中，构成一个完整的微型计算机。常用的单片机：51单片机，STM32单片机

1.2 最小系统板的构成：复位电路图示

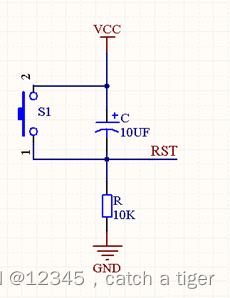
复位：指使系统回到初始状态，重新开始执行程序。不同MCU的复位电平可能不同，比如51单片机为高电平复位，STM32为低电平复位。为防止系统正常执行过程中误触，复位需要一定的时间的电平持续（比如0.1S）才会被判定复位。）图中为高电平复位，电阻可以看成下拉电阻

软件复位：32单片机可以使用看狗或者特定的函数进行软件复位。

上电复位：由于上电时电容中电荷为零，存在电容从0V充至5V的过程，此时电阻的RST从5V降至0V。由于RST端高于1.5V视为高电平，所以实际上电容从0充至3.5的0.1S时间内会触发系统复位。

按键复位：当平时按键不动时，电容充满电，电阻没有电流所以没有压降，如图，RST引脚此时属于低电平。当按键按下时，电容瞬间放电，按键松开时其实相当于是一个上电过程，同上会触发复位（实际上，手动按键不加电容一定情况下也能正常复位，但存在不稳定性）

 1.3 时钟晶振


晶振振荡原理：晶振的主要部件是石英晶体，结构为石英薄片两侧涂抹导电银层。利用石英的压电效应（通电产生形变，形变又会发电），对石英晶体通交流电会产生形变，形变又产生电压，当外电路频率和晶体固有频率相同时，晶体的振幅最大，同时产生相当稳定的振荡（正弦波），利用这个正弦波为单片机提供稳定的时钟频率。 

1.4 常见开发板和单片机

树莓派4B：

Broadcom BCM2711, Quad core Cortex-A72 (ARM v8) 64-bit SoC @ 1.5GHz
Raspberry Pi(中文名为“树莓派”,简写为RPi，(或者RasPi / RPI) 是为学习计算机编程教育而设计)，只有信用卡大小的微型电脑，其系统基于Linux。
可以将树莓派理解为一台微型电脑，它与我们平时使用的电脑近乎相同。

Arduino：

AVR单片机、ARM芯片
Arduino是一款便捷灵活、方便上手的开源电子原型平台。
它构建于开放原始码simple I/O介面版，并且具有使用类似Java、C语言的Processing/Wiring开发环境。主要包含两个的部分：硬件部分是可以用来做电路连接的Arduino电路板；另外一个则是Arduino IDE，你的计算机中的程序开发环境。只要在IDE中编写程序代码，将程序上传到Arduino电路板后，程序会告诉Arduino电路板要做什么。
简单来说，arduino是对单片机的二次封装。

Stm32:

ARM Cortex-M内核单片机
stm32全称是意法半导体32位系列微控制器芯片。STM32系列专为要求高性能、低成本、低功耗的嵌入式应用设计的ARM Cortex®-M0，M0+，M3, M4和M7内核。
主流产品（STM32F0、STM32F1、STM32F3）、超低功耗产品（STM32L0、STM32L1、STM32L4、STM32L4+）、高性能产品（STM32F2、STM32F4、STM32F7、STM32H7）

51单片机：

51单片机是对兼容英特尔8051指令系统的单片机的统称
51单片机广泛应用于家用电器、汽车、工业测控、通信设备中。因为51单片机的指令系统、内部结构相对简单，所以国内许多高校用其进行单片机入门教学。
51单片机是Intel在1981年推出的由8031微控制器芯片改造升级的、使用CISC指令集的、冯诺依曼架构的、8位的8051微控制器。后Intel将8051微控制器的内核授权给其他芯片厂商,使得市面上广泛出现类似于8051的芯片,这种采用8051内核的芯片被简称为51。
从上述例子中我们能直观地看到这些开发板和单片机所使用处理器的不同，但是树莓派、Arduino、stm32和我们日常使用的手机均是使用arm架构的处理器。

1.5 学习资料

1：B站 郭天祥，唐老师讲电赛

2：CSDN：小鱼教你模数电，乙酸氧铍，优信电子

3：硬件：硬创社

4：数据手册：半岛小芯

1.6 参考文献

https://blog.csdn.net/weixin_44161383/article/details/103593337

https://blog.csdn.net/florence_jz/article/details/129729236

https://blog.csdn.net/qq_57707070/article/details/128664070

二 计算机语言

2.1 我们知道最简单的计算机也必须有两个零件组成，CPU（指令处理器）和RAM（指令存储器），比如常见的手机，电脑最重要的性比就是cpu的处理速度，和ram的容量。

2.2 数据在计算机中是以二进制的形式存储的，不管我们传输什么内容，最终会编译成二进制才能被机器识别，所以从用户界面到机器语言是有一个过程的：

​

2.3  既然二进制是存储在内存中的，那计算机是怎样找到这个二进制数据呢，这就涉及到内存地址的概念。我们每定义一个变量，都会在内存中分配一个空间，这个空间会根据数据的大小占据不同的二进制位数。为了更方便的计算数据大小，我们通常用字节来表示数据大小，1byte=8位二进制。

2.4 那么内存具体是怎样分配字节空间的呢，内存实际上是按照容量大小分成有序字节数组，每个字节有唯一的内存地址。如下图，4G容量的内存就会分成2^32 个字节，然后按顺序定义字节编号

​

 2.5 通常我们使用的电脑或者手机经常会听到32位和64位的，那这32位和64位跟什么有关呢，这其实跟cpu指令集有关，代表着cpu一次能处理数据的最大位数，即也表示着cpu对内存的寻址能力，32 位操作系统对内存寻址不能超过 4GB，64 位操作系统对内存寻址可以超过 4GB。所以在工作频率相同的情况下，64位处理器的处理速度会比32位的更快。

三 C/C++中的指针

3.1 指针是什么？上面内容我们说了内存地址的概念，以及CPU处理指令是一个寻址的过程。那在C/C++中怎样获取这个地址编号呢，这就涉及到指针，我们可以定义一个指针变量，指向这个内存地址，就可以获取地址编号和地址数据

3.2 指针变量从定义上看与普通变量并没有区别，都是赋值用的，都需要类型和变量名，只不过普通变量指向数据，指针变量指向数据的地址。如下分别定义整型变量a和指针变量p

int a;//定义普通整型变量
int *p;//定义整型指针变量

3.3 我们每定义一个变量，就会在内存中分配一个地址，比如我们定义两个整形变量，可以打印下这两个变量的地址：

#include <iostream>
using namespace std;
int main() {
    int a=10;
    int b=10;
    printf("&a:0x%x\n",&a);
    printf("&b:0x%x\n",&b);
    return 0;
}

如下变量a和b的地址是不一样的

​

 3.4 指针的使用，既然是指针变量，就把指针指向已经存在的内存地址。如下：p指针指向a的地址

#include <iostream>
using namespace std;
int main() {
    int var_runoob=10;//定义普通整型变量
    int *p;//定义整型指针变量
    p = &var_runoob;//在指针变量中存储var_runoob的地址
    printf("&a:0x%x\n",&var_runoob);
    printf("&p:0x%x\n",p);
    return 0;
}

可以看到a和p的地址是一样的

​

 指针赋值过程图：p本身就是一个地址变量，所以不用在用&符号取地址了

​

 3.5 指针的运算

指针的加减和我们正常的加减有所区别，因为指针是地址变量，自增自减也是地址的运算

比如对指针变量 p 进行 p++、p--、p + i 等操作，所得结果也是一个指针，只是指针所指向的内存地址相比于 p 所指的内存地址前进或者后退了 i 个操作数

​

示例：定义一个p地址变量，然后自增

#include <iostream>
using namespace std;
int main() {
    int *p;
    printf("&p2:0x%x\n", p);
    p++;
    printf("&p2:0x%x\n", p);
    p++;
    printf("&p2:0x%x\n", p);
    p++;
    printf("&p2:0x%x\n", p);
    return 0;
}

 打印可以看到地址每次增加了4个字节，这是因为一个int类型占4个字节

​

3.6 非法指针，空指针，不指向任何东西。如下定义一个空指针：

#include <iostream>
using namespace std;
int main() {
    int *p=NULL;
    printf("&p:0x%x\n",p);
    return 0;
}

控制台输出指针p的地址是0，0即代表不指向任何内存

在大多数的操作系统上，程序不允许访问地址为 0 的内存，因为该内存是为操作系统保留的。但是，内存地址 0 有一个特别重要的意义，它表明改指针不指向一个可访问的内存位置

3.7 野指针，指针指向的位置不可知。

原因：

  • 指针未被初始化
  • 指针越界访问
  • 指针指向的空间释放

规避：

  • 注意数组不要越界访问
  • 及时把指针赋成空指针
  • 避免返回局部变量的地址
  • 使用指针前检查有效性

示例：

#include <iostream>
using namespace std;

//指针函数，返回变量a的地址
int* test( ) {
    int a = 5;
    return &a;
}

int main() {
    //定义指针变量P,指向a的地址
    int* p = test();
    printf("&p:0x%x\n",p);
    return 0;
}

打印后看到指针p的地址也是0，没指向任何内存

变量a的地址只在test()函数内有效，当把a的地址传给指针p时，因为出了test函数，变量a的空间地址释放，导致p变成了野指针。

 3.8 二级指针，即指向指针的指针，也可以说指针的类型是指针。

#include <iostream>
using namespace std;
int main() {
    int a = 10;
    int* p= &a;//p是int类型的一级指针
    int** pp= &p;//pp是存放的一级指针的地址

    printf("&p:0x%x\n",p);
    printf("&p:0x%x\n",&p);
    printf("&p:0x%x\n",pp);
    //int*** ppp =&pp;//这里的ppp就是三级指针
    return 0;
}

打印可以看到 二级指针pp和一级指针*p的地址一样，说明pp存放的是一级指针p的地址

 3.9 数组指针，是一个指针，它指向一个数组，指针的地址是数组的首元素地址

#include <iostream>
using namespace std;
int main() {
    int a[3]= {1,2,3};// 声明一个int类型的数组，这个数组有3个元素
    int *p = a;// 声明一个int类型的指针变量.指向a数组

    printf("&a:0x%x\n\n",&a);

    printf("&a[0]:0x%x\n",&a[0]);
    printf("&a[1]:0x%x\n",&a[1]);
    printf("&a[2]:0x%x\n\n",&a[2]);

    printf("&a[2]:0x%x\n",p);

    return 0;
}

 打印可以看到，数组变量a的地址是数组第0个元素的地址，指针p也是数组首元素的地址

3.10 指针数组，是一个数组，数组中的每一个元素都是指针。数组取地址是首元素指针的地址

#include <iostream>
using namespace std;
int main() {
    int* p[3];//声明一个指针数组，该数组有10个元素，其中每个元素都是一个指向int类型的指针

    printf("&p[0]:0x%x\n",&p[0]);
    printf("&p[1]:0x%x\n",&p[1]);
    printf("&p[2]:0x%x\n",&p[2]);

    printf("&p:0x%x\n",p);
    return 0;
}

可以看到 数组的地址和第一个元素的指针地址是一样的。

四 二进制在计算机中的使用

4.1 有符号数和无符号数，用来表示正数和负数。最高位（第一位）是符号位，正数符号位为“0” ，负数符号位为“1” 。如 1和-1表示为如下

0000 0001
1000 0001

4.2 原码

就是机器数，是加了一位符号位的二进制数，因为数值有正负之分

如1和-1的原码表示为如下：

0000 0001
1000 0001

4.3 反码

带符号位的原码乘除运算时结果正确，而在加减运算的时候就出现了问题。

比如: 用十进制表示:1 + (-1) = 0, 但用二进制表示：

00000001 + 10000001 = 10000010

将结果换算成十进制数也就是 -2。于是在原码的基础上发明了反码,用来解决这种问题。

如 1和-1反码表示为如下：

0000 0001
1111 1110

4.4 补码

虽然反码的出现解决了正负数的加减问题, 但却让0这个数字有了两种"形态": “0"和”-0"，
但这是不合逻辑的，只应该有一个0，所以出现了补码

正数的补码就是其本身

负数的补码是在其原码基础上, 符号位不变, 其余各位取反, 最后+1(等同于在反码的基础上+1)，如 1和-1反码表示为如下：

0000 0001
1111 1111

总结：

1、正数的原码、反码、补码都一样；
2、负数的反码 = 它的原码符号位不变，其他位取反 (取反的意思：0 换成 1 ，1 换成 0 )；
3、负数的补码 = 它的反码 +1；
4、0的反码、补码都是0；
5、在计算机运算的时候，都是以 补码 的方式来运算的 。
6、二进制 转为 十进制，必须使用 二进制 的原码进行转换 。

4.5 示例

使用“有符号数”来模拟一下，在计算机中是怎样运算的

正数相加：

例如：1+1 ，在计算机中运算如下：

1的原码为：

00000000 00000000 00000000 00000001

因为“正数的原码、反码、补码都一样”，所以，1的补码 = 1的原码，所以 1的补码+ 1的补码 就等于：

00000000 00000000 00000000 00000001
+
00000000 00000000 00000000 00000001

=

00000000 00000000 00000000 00000010

00000000 00000000 00000000 00000010（ 转换为10进制） = 2

正数相减：

例如：1 - 2，在计算机中运算如下：

在计算机中减运算其实是作为加运算来操作的，所以，1 - 2 = 1 + ( -2 )

第一步：把 1的补码找出来（因为正数的原码、反码、补码都一样，所以我们可通过原码直接获取补码）：

1的补码：

00000000 00000000 00000000 00000001

第二步：把-2的原码找出来：

-2的原码：

10000000 00000000 00000000 00000010

第三步：把-2的反码找出来：

-2的反码：

11111111 11111111 11111111 11111101

第三步：把-2的补码找出来：

-2的补码：

11111111 11111111 11111111 11111110

第四步：1的补码与-2的补码相加：

00000000 00000000 00000000 00000001
+
11111111 11111111 11111111 11111110

=

11111111 11111111 11111111 11111111

第五步：将计算结果的补码转换为原码，反其道而行之即可（如果想将二进制转换为十进制，必须得到二进制的原码）

补码：11111111 11111111 11111111 11111111

=

反码：11111111 11111111 11111111 11111110

=

原码：10000000 00000000 00000000 00000001

第六步：将计算结果的二进制原码 转换 为十进制

二进制原码：10000000 00000000 00000000 00000001 = 1*2^0 = -1

4.6 java中为什么byte的取值范围是-128~127

java中byte占一个字节, 也就是8bit(位)， 其中最高位是符号位，剩下7位用来表示数值。

若符号位为0， 则表示为正数，范围为00000000~01111111(补码形式)，也就是十进制的0-127。

若符号位为1， 则表示为负数， 范围为10000000~11111111(补码形式)， -128~-1， 11111111转换为原码就是10000001，也就是-1。

在补码中,为了避免存在"-0"，规定10000000为-128，所以解释了byte的取值范围为什么是-128~127。

4.7 Java中的<< 和 >> 和 >>>

首先<< 和 >> 和 >>>是java中的位运算符，是针对二进制进行操作的。

除了这些还有&、|、^、~、几个位操作符。不管是初始值是依照何种进制，都会换算成二进制进行位操作。

Java中的<< 表示左移移，不分正负数，低位补0。

以下数据类型默认为byte为8位，左移时不管正负，低位补0

正数：r = 20 << 2

20的二进制补码：0001 0100

向左移动两位后：0101 0000

结果：r = 80

负数：r = -20 << 2

-20 的二进制原码 ：1001 0100

-20 的二进制反码 ：1110 1011

-20 的二进制补码 ：1110 1100

左移两位后的补码：1011 0000

反码：1010 1111

原码：1101 0000

结果：r = -80

Java中的‘ >> ’表示右移，如果该数为正，则高位补0，若为负数，则高位补1；

注：以下数据类型默认为byte为8位

正数：r = 20 >> 2　

20的二进制补码：0001 0100

向右移动两位后：0000 0101

结果：r = 5

负数：r = -20 >> 2　

-20 的二进制原码 ：1001 0100

-20 的二进制反码 ：1110 1011

-20 的二进制补码 ：1110 1100

右移两位后的补码：1111 1011

反码：1111 1010

原码：1000 0101

结果：r = -5

‘ >>> ’ 表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位同样补0　

注：以下数据类型默认为int 32位

正数：　r = 20 >>> 2

的结果与 r = 20 >> 2 相同；

负数：　r = -20 >>> 2

-20原码：10000000 00000000 00000000 00010100

反码：11111111 11111111 11111111 11101011

补码：11111111 11111111 11111111 11101100

右移：00111111 11111111 11111111 11111011

结果：r = 1073741819

五  进制间转换

5.1 常见的进制

十进制：

十进制是Decimal，简写为D
都是以0-9这九个数字组成。


二进制：

二进制是Binary，简写为B
由0和1两个数字组成。


八进制：

八进制是Octal，简写为O
由0-7数字组成，为了区分与其他进制的数字区别，开头都是以0开始。


十六进制：

十六进制为Hexadecimal，简写为H
表示方式为0x开头
计数到F后，再增加1个，就进位。
由0-9和A-F组成，英文字母A，B，C，D，E，F分别表示数字10～15。

123456789ABCDEF
123456789101112131415

5.2 十进制转二进制

十进制数除2取余法，即十进制数除2，余数为权位上的数，得到的商值继续除2，依此步骤继续向下运算直到商为0为止

如下图：把150转为二进制是：10010110

 5.3 二进制转十进制

把二进制数按权展开、相加即得十进制数.如下图10010110转为十进制是：150

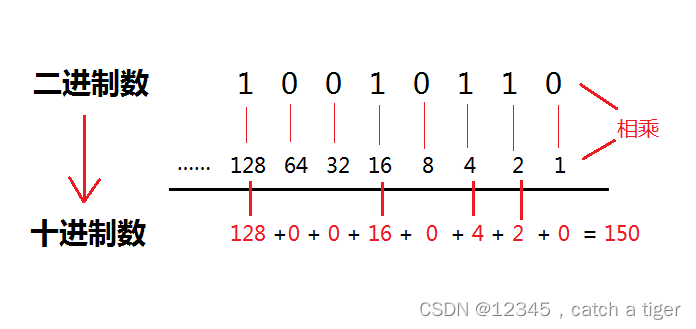
 5.4 基础的二进制和十进制对应关系

关注二进制1所在的位置1234
二进制0001001001001000
十进制1248
与二的次方的关系20212223

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/509694.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

centos7安装nginx

centos7安装nginx

1.配置环境 1).gcc yum install -y gcc2).安装第三方库 pcre-devel yum install -y pcre pcre-devel3).安装第三方库 zlib yum install -y zlib zlib-devel2.下载安装包并解压 nginx官网下载&#xff1a;http://nginx.org/en/download.html 或者 使用wget命令进行下载 wg…
阅读更多...
第一期 | ICASSP 2023 论文预讲会

第一期 | ICASSP 2023 论文预讲会

ICASSP 2023 论文预讲会是由CCF语音对话与听觉专委会、语音之家主办&#xff0c;旨在为学者们提供更多的交流机会&#xff0c;更方便、快捷地了解领域前沿。活动将邀请 ICASSP 2023 录用论文的作者进行报告交流。 ICASSP &#xff08;International Conference on Acoustics, …
阅读更多...
GraphHopper调研笔记

GraphHopper调研笔记

一、 GraphHopper GraphHopper是一种快速且内存有效的Java导航引擎&#xff0c;默认使用OSM和GTFS数据&#xff0c;也可导入其他的数据源。支持CH&#xff08;Contraction Hierarchies&#xff09;、A*、Dijkstra算法。 1、应用介绍 graphhopper有以下几种常见的地图应用&am…
阅读更多...
AI 不会取代打工人，使用 AI 的人才会

AI 不会取代打工人，使用 AI 的人才会

一、被AI端掉饭碗之前&#xff0c;提升自己的硬核实力 AI工具带来了工业革命级别的效率提升&#xff0c;除了强大&#xff0c;更多的引发了打工人的集体焦虑&#xff1a;“我的活ai都能干了&#xff0c;那我做什么呢&#xff1f;” 当然&#xff0c;还有另一种更积极的解答&a…
阅读更多...
C语言中变量的默认初始值

C语言中变量的默认初始值

在对数组元素求和时&#xff0c;竟然离奇的发现错了&#xff0c;冲了一会儿浪之后才现在问题在这里 main函数代码&#xff1a; int main(void){int arr[5] {1,2,3,4,5};int res sum(arr,arr5);printf("%d",res); }求和函数&#xff08;利用双指针求的数组元素之和…
阅读更多...
第8章 虚拟主机

第8章 虚拟主机

第8章 虚拟主机 虚拟主机&#xff0c;就是把一台物理服务器划分成多个“虚拟”的服务器&#xff0c;这样我们的一台物理服务器就可以当做多个服务器来使用&#xff0c;从而可以配置多个网站。 Nginx提供虚拟主机的功能&#xff0c;就是为了让我们不需要安装多个Nginx&#xf…
阅读更多...
2023年8月24-25日｜2023中国绿色数据中心峰会

2023年8月24-25日｜2023中国绿色数据中心峰会

2023中国绿色数据中心峰会 会议背景 应对气候变化已经成为21世纪人类社会面临的紧迫挑战&#xff0c;推进绿色发展成为全球共识。2021年12月&#xff0c;国家发改委等四部门印发的《贯彻落实碳达峰碳中和目标要求推动数据中心和5G等新型基础设施绿色高质量发展实施方案》提出…
阅读更多...
QT MD4 MD5 Sha1等几种加密方式

QT MD4 MD5 Sha1等几种加密方式

QT MD4 MD5 Sha1等几种加密方式 [1] QT MD4 MD5 Sha1等几种加密方式[2] qt MD5 和AES 加密一 、MD5 加密二、AES 加密和解密 [3] QT中sqlite数据库数据加密/混淆---MD5/SHA1/SHA2/SHA3&#xff08;1&#xff09;创建一个加密对象&#xff08;2&#xff09;放入要加密的数据&…
阅读更多...
嘉立创EDA PDF文件的输出教程

嘉立创EDA PDF文件的输出教程

在PCB生产调试期间&#xff0c;为了方便查看文件或者查询相关元件信息&#xff0c;会把PCB设计文件转换成PDF文件。下面介绍常规PDF文件的输出方式。 前期工作是需要在电脑上安装PDF阅读器&#xff0c;准备充足后按照以下步骤进行操作。 1&#xff09;执行菜单命令“导出-PDF…
阅读更多...
企业财务管理为何需要数字化转型？

企业财务管理为何需要数字化转型？

为什么企业财务管理需要数字化转型&#xff1f; 许多企业在推动各大业务部门进行数字化转型时&#xff0c;往往会忽略财务部门。然而&#xff0c;作为掌握公司核心资源与数据和推动企业数字化建设的部门&#xff0c;财务也应成为企业数字化转型的重要突破口。 这篇就用几个案…
阅读更多...
用Leangoo领歌Scrum敏捷开发工具管理产品路线图？

用Leangoo领歌Scrum敏捷开发工具管理产品路线图？

那我们来看下&#xff0c;如何利用Leangoo管理产品路线图&#xff1f; 首先什么是产品路线图&#xff1f; 产品路线图是一个高层次的战略计划&#xff0c;它描述了产品在未来一段时间可能会如何发展和壮大。 产品路线图确保整个产品团队持续关注产品的目标&#xff0c;帮助产…
阅读更多...
07-微服务部署2023系列-centos+docker部署nacos

07-微服务部署2023系列-centos+docker部署nacos

1、创建nacos的数据库配置 1.1、创建数据库 1.2、创建用户nacos并授权数据库 参考 06 mysql 创建账户部分内容 1.3、执行数据库脚本 导入官方nacos sql语句。如果是历史有历史数据&#xff0c; 从历史数据sql导入 2、创建 bridge 网络并指定 IP 区间 2.1、创建自定义网络…
阅读更多...
第十章 使用Samba或NFS实现共享文件

第十章 使用Samba或NFS实现共享文件

文章目录 第十章 使用Samba或NFS实现共享文件一、SAMBA文件共享服务1、SAMBA简介2、相关配置&#xff08;1&#xff09;、安装软件&#xff08;2&#xff09;、删除多余配置文件&#xff08;3&#xff09;、Samba服务验证方式 3、配置共享资源&#xff08;1&#xff09;、用于设…
阅读更多...
认识 AbortController控制器对象 及其应用

认识 AbortController控制器对象 及其应用

参考文章1 参考文章2 一、什么是AbortController (abort 意为 中止/废弃) AbortController是一个控制器对象&#xff08;DOM API&#xff09;&#xff0c;可通过new构造函数的方式&#xff0c;生成控制器实例对象&#xff0c;根据需要终止/取消一个或多个Web请求/监听事件 通…
阅读更多...
微信开发者工具突然打不开问题解决

微信开发者工具突然打不开问题解决

今天微信小程序开发者工具 好好的在电脑里 突然就打不开了 这个问题已经上百度了 想必并不是很少遇到 可能是版本太旧 或者 其中依赖文件丢失 这个基本不用抱什么幻想 还是得重新装 先将快捷打开方式删掉 然后找到工具所在目录 把它删了 然后访问如下地址 https://mp.weixi…
阅读更多...
日期时间选择器el-date-picker，限制可选范围，以后端接口某个时间字段为时间节点

日期时间选择器el-date-picker，限制可选范围，以后端接口某个时间字段为时间节点

哈喽 大家好啊 今天需要做一个时间选择器的限制&#xff0c;不然用户选择某个时间节点之前的时间 比如用户选择发货时间不允许早于收货时间&#xff08;来自后端接口&#xff09; picker-options当前时间日期选择器特有的选项参考下表object 首先申明一个时间可选对象 因为我…
阅读更多...
黑马程序员-学成在线项目总结

黑马程序员-学成在线项目总结

黑马程序员-学成在线项目总结 收获 基础公共样式 清除默认样式&#xff0c;例如内边距、外边距、项目符号等等 设置通用样式&#xff0c;例如&#xff1a;文字样式 项目结构 注:多个css文件引入顺序&#xff0c;先清除&#xff0c;后设置 版心效果 许多网页整体都有版心居…
阅读更多...
Java框架学习01（Spring框架）

Java框架学习01（Spring框架）

1、什么是Spring框架&#xff1f; Spring 是一款开源的轻量级 Java 开发框架&#xff0c;旨在提高开发人员的开发效率以及系统的可维护性。 我们一般说 Spring 框架指的都是 Spring Framework&#xff0c;它是很多模块的集合&#xff0c;使用这些模块可以很方便地协助我们进行…
阅读更多...
网络漏洞管理

网络漏洞管理

网络漏洞是硬件、软件或流程中的漏洞或缺陷&#xff0c;可能威胁到网络的正常运行。漏洞会使您的业务和客户的敏感数据面临风险&#xff0c;导致黑客轻松进入、销售额下降、声誉损失和处罚。网络漏洞可以分为硬件、固件、软件和人类漏洞。如果这些实体中的任何一个没有得到适当…
阅读更多...
关于Kerberos认证的一些攻击手法学习总结

关于Kerberos认证的一些攻击手法学习总结

Kerberos认证流程 前言 本文主要分享最近学习的关于域内Kerberos认证的一些攻击手法&#xff0c;以自我的理解为主&#xff0c;从原理理解切入到基本工具利用来阐述&#xff0c;个人的理解分析较为啰嗦&#xff0c;嫌太兀长的可以跳着看就好&#xff0c;还请各位谅解。如有错误…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023