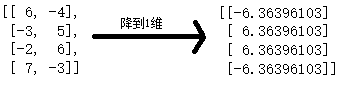
数字签名基本概念
- R1:receiver确认、证实sender的签名,这个签名不能被伪造
- S:sender发送出签名的教习给receiver,不能否认他签发的消息
- R2:receiver堆收到的签名消息不能否认,收报认证
- T:第三方可以确认手法收发双方之间的消息传输,但不可伪造
与消息认证的区别:
消息认证:只用于防范第三者破坏,未验证sender身份(RS双方没有利害冲突)
- receiver验证sender身份是否被篡改
- receiver验证消息是否被篡改
数字签名:(RS双方存在利害冲突)
- 数字签名确定消息来源的真实性
- 数字签名保证实体身份的真实性
- 不可否认
与公钥加密的区别
公钥
- A用B公开密钥加密data后,发送data(已加密)给B
- B用私钥堆密文解密得到明文
签名
- A用私钥加密消息m签名,将m与签名发送给B
- B 收到A签名,使用A公钥验证签名有效性
- 签名消息可能要多年以后验证
- 签名可能要多次严正
- 签名安全性、防伪造要求高
- 签名速度要比验证速度快
分类
消息是否被压缩分类:
- 对整体消息签名
- 对压缩的消息签名
按消息/签名对应关系划分
- 确定性deterministic数字签名:消息与签名一一对应。对同意消息签名永不变化 —— RSA/Rabin算法
- 随机化 randomized
构成
- 签名算法 signature algorithm
- 验证算法 verification algorithm
安全性约定: 签名算法、密钥是秘密的,只有签名人掌握;验证算法公开
签名
( M , S , K , V ) (M,S,K,V) (M,S,K,V)
- M 明文空间
- S 签名集合
- K 密钥空间
- V 验证函数的值域, 真、伪组成
∀ k ∈ K , m ∈ M 签名算法 : s = S i g k ( m ) ∈ S 验证算法 : V e r l ( s , m ) ∈ { t r u e , f a l s e } \forall k\in K, m\in M\\签名算法:s = Sig_k(m)\in S \\ 验证算法: Ver_l(s,m)\in\{true, false\} ∀k∈K,m∈M签名算法:s=Sigk(m)∈S验证算法:Verl(s,m)∈{true,false}
安全性:m和s很难推出签名者私钥 k k k,很难伪造信息 m ′ m' m′使得 V e r k ( s , m ′ ) = t r u e Ver_k(s,m') = true Verk(s,m′)=true
签名体制
RSA数字签名
参数同之前讲过的RSA
n = p ∗ q n = p * q n=p∗q
选e计算出d让 e d ≡ 1 m o d ϕ ( n ) ed \equiv 1\ mod\ \phi(n) ed≡1 mod ϕ(n)
n和e公开,p,q,d保密
RSA密码:
c
=
m
e
c = m ^ e
c=me
∀
m
∈
Z
n
,
签名
s
=
S
i
g
k
(
m
)
=
m
d
m
o
d
n
\forall m \in Z_n, 签名s = Sig_k(m) = m^d\ mod\ n
∀m∈Zn,签名s=Sigk(m)=md mod n
验证真实性:签名者才知道私钥d,其他人难以伪造
m
≡
s
e
m
o
d
n
m\equiv s^e\ mod \ n
m≡se mod n
Rabin
N
=
p
q
N = pq
N=pq。 p和q都是大质数
m
,
s
∈
Q
R
p
∩
Q
R
q
m,s\in QR_p\cap QR_q
m,s∈QRp∩QRq QR是二次剩余集
pq密钥,N公钥
签名过程
- 消息 m , 0 < m < N , m ∈ Q R p ∩ Q R q 消息m, 0<m<N,m\in QR_p\cap QR_q 消息m,0<m<N,m∈QRp∩QRq
- s = S i g k ( m ) = m m o d ( p × q ) s = Sig_k(m) = \sqrt{m}\ mod\ (p\times q) s=Sigk(m)=m mod (p×q)
验证过程
m ≡ s 2 m o d N m\equiv s^2\ mod \ N m≡s2 mod N
二次剩余集
n为正整数,整数a满足
g
c
d
(
a
,
n
)
=
1
gcd(a,n) = 1
gcd(a,n)=1
x
2
=
a
m
o
d
n
有解
x^2=a\ mod \ n有解
x2=a mod n有解
a为mod n的平方剩余
如选n=7
x
2
=
1
m
o
d
7
x
=
1
/
6
x^2=1\ mod \ 7\quad x = 1/6
x2=1 mod 7x=1/6
x
2
=
2
m
o
d
7
x
=
3
/
4
x^2=2\ mod \ 7\quad x = 3/4
x2=2 mod 7x=3/4
x
2
=
3
m
o
d
7
无解
x^2=3\ mod \ 7\quad 无解
x2=3 mod 7无解
x
2
=
4
m
o
d
7
x
=
2
/
5
x^2=4\ mod \ 7\quad x = 2/5
x2=4 mod 7x=2/5
x
2
=
5
m
o
d
7
无解
x^2=5\ mod \ 7\quad 无解
x2=5 mod 7无解
x
2
=
6
m
o
d
7
无解
x^2=6\ mod \ 7\quad 无解
x2=6 mod 7无解
1, 2, 4是 mod 7的二次剩余,且每个二次剩余有两个平方根
3, 5, 6是 mod 7的非二次剩余
ELGamal
参数
- p 大素数,在 Z p Z_p Zp中求解离散对数十分困难
- g 群 Z p ∗ Z_p^* Zp∗的一个生成元或本原元素
- M 消息空间 Z p ∗ Z_p^* Zp∗
- S 签名空间 Z p − 1 Z_{p-1} Zp−1
- x 用户密钥 x ∈ Z p ∗ x\in Z_p^* x∈Zp∗
- y 用户公钥 y ≡ g x m o d p y\equiv g^x\ mod \ p y≡gx mod p
p,g,y公钥,x密钥
签名过程
- 选择随机数 k ∈ Z p ∗ m ∈ M k\in Z_p^*\quad m\in M k∈Zp∗m∈M
- 得到 H ( m ) H(m) H(m)
- 得到 r = g k m o d p r = g^k\ mod\ p r=gk mod p
- 得到 s = [ H ( m ) − x r ] k − 1 m o d ( p − 1 ) s = [H(m) - xr]k^{-1} \ mod\ (p-1) s=[H(m)−xr]k−1 mod (p−1)
- 得到签名 S i g k ( m ) = ( r , s ) , m 与 ( r , s ) Sig_k(m)=(r,s), m与(r,s) Sigk(m)=(r,s),m与(r,s)发给对方
验证过程
- 得到 m 与 ( r , s ) m与(r,s) m与(r,s)
- 计算 H ( m ) H(m) H(m)
- 验证
V e r k ( H ( m ) , ( r , s ) ) = = t r u e ⇔ y r r s = g H ( m ) m o d p Ver_k(H(m), (r,s)) == true \Leftrightarrow y^rr^s=g^{H(m)}\ mod\ p Verk(H(m),(r,s))==true⇔yrrs=gH(m) mod p
( r x + s k ) = H ( m ) m o d ( p − 1 ) (rx+sk)=H(m)\ mod\ (p-1) (rx+sk)=H(m) mod (p−1)
得到
y r r s = g H ( m ) m o d p y^rr^s=g^{H(m)}\ mod\ p yrrs=gH(m) mod p
Example
- p = 467, g = 2, x = 127
- 得到 y = g x = 2 127 = 132 m o d 467 y = g^x = 2^{127}=132 \ mod\ 467 y=gx=2127=132 mod 467
- 得到m的哈希值 H ( m ) = 100 H(m)=100 H(m)=100,选随机数k = 213 (注意213和466互质,且 21 3 − 1 = 431 m o d 466 213^{-1} = 431\ mod \ 466 213−1=431 mod 466)
- 有 r = 2 213 = 29 m o d 467 r = 2^{213}=29\ mod\ 467 r=2213=29 mod 467 s = ( 100 − 127 × 29 ) × 431 = 51 m o d 466 s = (100-127\times 29)\times 431 = 51\ mod\ 466 s=(100−127×29)×431=51 mod 466
- 验证:收信人计算出 H ( m ) = 100 H(m) = 100 H(m)=100, 13 2 29 2 9 51 = 189 m o d 467 132^{29}29^{51}=189\ mod\ 467 132292951=189 mod 467, 2 100 = 189 m o d 467 2^{100}=189\ mod\ 467 2100=189 mod 467
安全性
不知道<消息,签名>对的时候,伪造签名 近似 求离散对数
Attacker若掌握同一随机数k下两个消息
m
1
,
m
2
m_1,m_2
m1,m2的合法签名
(
r
1
,
s
1
)
,
(
r
2
,
s
2
)
(r_1,s_1),(r_2,s_2)
(r1,s1),(r2,s2)会构造如下方程
m
1
=
r
1
x
+
s
1
k
m
2
=
r
2
x
+
s
2
k
m_1=r_1x+s_1k\\ m_2=r_2x+s_2k
m1=r1x+s1km2=r2x+s2k
攻击者解此房产可求出x和k
确保安全性需要选签名的时候选择不同随机数k
Schnorr签名体制
参数
- q,p 大素数,q|p-1, 在 Z p Z_p Zp中求解离散对数 十分困难
- g Z p Z_p Zp中乘群 Z p ∗ Z_p^* Zp∗的一个元素,满足 g q = 1 m o d p g^q = 1\ mod\ p gq=1 mod p
- M 消息空间, Z p ∗ Z_p^* Zp∗
- S 签名空间 Z p ∗ × Z p − 1 Z_p^*\times Z_{p-1} Zp∗×Zp−1
- x 用户密钥 1 < x < q 1 < x < q 1<x<q
- y 用户公钥 y ≡ g x m o d p y\equiv g^x\ mod \ p y≡gx mod p
p,q,g,y公钥,x密钥
过程
- user 使用随机数 k ∈ Z q , m ∈ M k\in Z_q, m\in M k∈Zq,m∈M
- 计算 w = g k m o d p w=g^k\ mod\ p w=gk mod p
- 计算 r = H ( w ∣ ∣ m ) r = H(w||m) r=H(w∣∣m) ||表示拼接
- 计算 s = k + x r m o d p s = k+xr\ mod\ p s=k+xr mod p
- 签名 S i g k ( m ) = ( r , s ) Sig_k(m)=(r,s) Sigk(m)=(r,s)作为签名,将m和 ( r , s ) (r,s) (r,s)送给对方
验证
- 收到消息 m m m和签名 ( r , s ) (r,s) (r,s)
- 计算 H ( m ) H(m) H(m)
- 计算 w ′ = g s y − r m o d p w' = g^s y^{-r}\ mod\ p w′=gsy−r mod p
- 计算 H ( w ′ ∣ ∣ m ) H(w'||m) H(w′∣∣m)
- 验证 H ( w ′ ∣ ∣ m ) = r , 即 V e r ( y , ( e , s ) , m ) = t r u e H(w'||m) = r, 即Ver(y,(e,s),m) = true H(w′∣∣m)=r,即Ver(y,(e,s),m)=true
安全性
Schnorr与ElGamal区别
- E体制中,g是 Z p Z_p Zp本原元素;S体制中,g是 Z p ∗ Z_p^* Zp∗中子集 Z q ∗ Z_q^* Zq∗的本原元,它不是 Z p ∗ 的本原元 Z_p^*的本原元 Zp∗的本原元
- S的签名比E短,由 ∣ q ∣ |q| ∣q∣和 ∣ H ( m ) ∣ |H(m)| ∣H(m)∣决定
- w = g k m o d p w = g^k\ mod\ p w=gk mod p可以预先计算,签名要一次乘法、一次加法,签名速度快,适合智能卡应用
- S签名短,安全性逊于E签名
DSS签名体制
DSA事故DSS签名标准中采用的数字签名算法
参数
- p 大素数, 2 L − 1 < p < 2 L 2^L-1<p<2^L 2L−1<p<2L, 512 ≤ L ≤ 1024 512\le L \le 1024 512≤L≤1024
- q:(p-1)的素因子,且 2 159 < q < 2 160 2^{159}<q<2^{160} 2159<q<2160 字长160b
- g g = h ( p − 1 ) / q m o d p g=h^{(p-1)/q}\ mod\ p g=h(p−1)/q mod p
- x 用户私钥 1 < x < q 1 < x < q 1<x<q
- y 用户公钥
y
=
g
x
m
o
d
p
y = g^x\ mod\ p
y=gx mod p
p,q,g,y公钥,x是私钥
签名
- user使用随机数
- 计算 H ( m ) H(m) H(m)
- 计算 r = ( g k m o d p ) m o d q r = (g^k\ mod\ p)\ mod\ q r=(gk mod p) mod q
- 计算 s = [ k − 1 ( H ( m ) + x r ) ] m o d q s = [k^{-1}(H(m)+xr)]\ mod\ q s=[k−1(H(m)+xr)] mod q
- 签名 S i g k ( m ) = ( r , s ) Sig_k(m) = (r,s) Sigk(m)=(r,s) 将m和(r,s)送给对方
验证
- 收到m与(r,s)
- H ( m ) H(m) H(m)
- w = s − 1 m o d q w=s^{-1}\ mod\ q w=s−1 mod q
- u 1 = [ H ( m ) w ] m o d q u_1 = [H(m)w]\ mod\ q u1=[H(m)w] mod q
- u 2 = r w m o d q u_2 = rw\ mod\ q u2=rw mod q
- v = [ ( g u 1 y u 2 ) m o d p ] m o d q v = [(g^{u1}y^{u2})\ mod\ p]\ mod\ q v=[(gu1yu2) mod p] mod q
- 验证 v = r v = r v=r
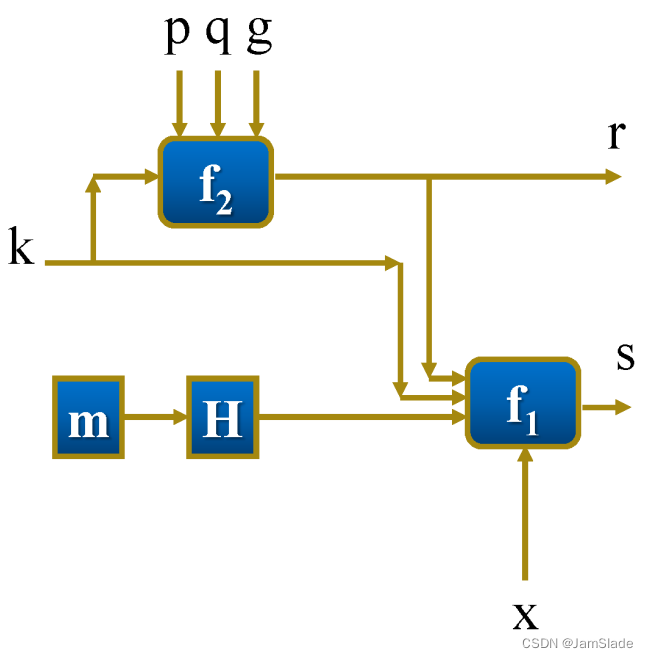
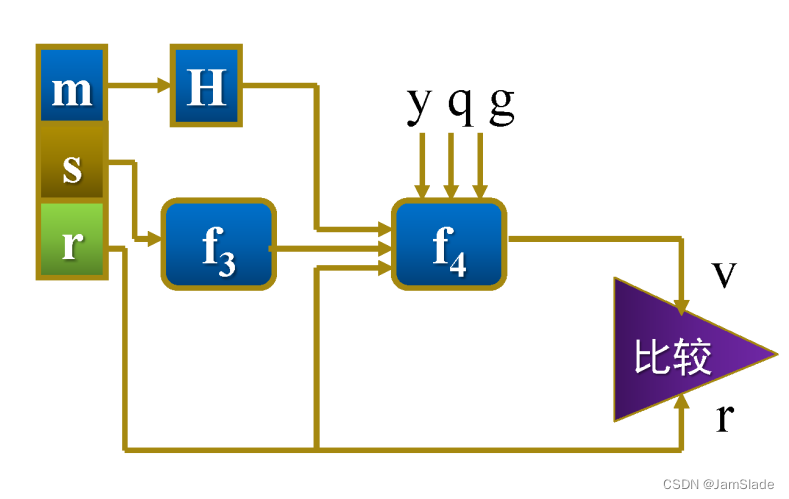
ESIGN
- n, n = p 2 q n = p^2q n=p2q大合数,公钥
- p,q 两个大素数
- M 消息空间
- S 命名空间
- k 安全参数
签名
- 选择随机数 $ 0<r<pq $
- 计算 H ( M ) H(M) H(M)
- 计算 w = 大于等于 [ ( H ( M ) − r k ) m o d n ] / p q w = 大于等于[(H(M) - r^k)\ mod\ n]/ pq w=大于等于[(H(M)−rk) mod n]/pq的最小整数
- 计算 s = r + [ ( w / k r k − 1 m o d p ) ] × p q s = r + [(w/kr^{k-1}\ mod\ p)]\times pq s=r+[(w/krk−1 mod p)]×pq
- S i g k ( M , k ) = s Sig^{k}(M,k)=s Sigk(M,k)=s作为签名,M和s送给对方
验证
- 收到M和s
- 计算 H ( M ) H(M) H(M)
- 计算 s r k m o d p s^{rk}\ mod\ p srk mod p
- 计算 a,它是大于等于 2 n / 3 2n/3 2n/3最小整数
- 验证 V e r k ( H ( M ) , s ) = t r u e ⇔ H ( M ) ≤ s k ∧ s k m o d n < H ( M ) + 2 a Ver_k(H(M),s) = true \Leftrightarrow H(M)\le s^k \land s^k\ mod\ n < H(M) + 2^a Verk(H(M),s)=true⇔H(M)≤sk∧sk mod n<H(M)+2a
算法可以用预计算提高签名速度
发送方预计算:
u
=
r
k
m
o
d
n
v
=
1
/
(
k
r
k
−
1
)
m
o
d
p
u = r^k\ mod\ n\quad v = 1/(kr^{k-1})\ mod\ p
u=rk mod nv=1/(krk−1) mod p
计算w:w = 大于等于 [ H ( M ) − u m o d n ] / p q [H(M)-u\ mod\ n]/pq [H(M)−u mod n]/pq的最小整数
计算s s = r + ( w v m o d p ) × p q s = r + (wv\ mod\ p)\times pq s=r+(wv mod p)×pq
通过预先计算,让速度提高十倍。K = 2,3会被破解,建议k = 8,16,32,64,128,256,1024
Okamoto
- p,q: 大素数,p至少512bit
- q: (p-1)的素因子,q长约140bit
- g1,g2:全局公钥,与q同长
- s1,s2:秘钥,与q同长
- M: 消息空间 M ∈ Z P ∗ M\in Z^*_{P} M∈ZP∗
- S: 签名空间 Z P ∗ × Z P − 1 Z_P^*\times Z_{P-1} ZP∗×ZP−1
- v: 用户公钥 v = g 1 − s 1 g 2 − s 2 m o d p v = g_1^{-s1}g_2^{-s2}\ mod\ p v=g1−s1g2−s2 mod p
- p,q,g1,g2,v公钥, s1,s2密钥
如何签名?
- 选随机数 r1,r2, 满足 0 < r 1 , r 2 < q 0 <r_1,r_2<q 0<r1,r2<q
- 算 e = H ( g 1 r 1 g 2 r 2 m o d p , M ) e = H(g_1^{r_1}g_2^{r_2}\ mod\ p, M) e=H(g1r1g2r2 mod p,M)
- 算 y 1 = ( r 1 + e s 1 ) m o d q y_1 = (r_1 + es_1)\ mod\ q y1=(r1+es1) mod q
- 算 y 2 = ( r 2 + e s 2 ) m o d q y_2 = (r_2 + es_2)\ mod\ q y2=(r2+es2) mod q
- S i g k ( M , k ) = S = ( e , y 1 , y 2 ) Sig_k(M,k)=S=(e,y_1,y_2) Sigk(M,k)=S=(e,y1,y2)做签名,M和S送给对方
g 1 y 1 g 2 y 2 v e m o d p = g 1 r 1 e s 1 g 2 r 2 r s 2 ( g 1 − s 1 g 2 − s 2 ) e m o d p = g 1 r 1 g 2 r 2 m o d p g_1^{y_1}g_2^{y_2}v^e\ mod\ p \\ =g_1^{r_1es_1}g_2^{r_2rs_2}(g_1^{-s1}g_2^{-s_2}) ^e\ mod\ p \\ = g_1^{r_1}g_2^{r_2}\ mod\ p g1y1g2y2ve mod p=g1r1es1g2r2rs2(g1−s1g2−s2)e mod p=g1r1g2r2 mod p
所以
H
(
g
1
y
1
g
2
y
2
v
e
m
o
d
p
,
M
)
=
H
(
g
1
r
1
g
2
r
2
m
o
d
p
,
M
)
=
e
H(g_1^{y_1}g_2^{y_2}v^e\ mod\ p, M) = H(g_1^{r_1}g_2^{r_2}\ mod\ p, M) = e
H(g1y1g2y2ve mod p,M)=H(g1r1g2r2 mod p,M)=e
OSS签名体制
- n 大整数
- k 随机数,满足(k, n) = 1
- h 满足 h = − k − 2 m o d n h = -k^{-2}\ mod\ n h=−k−2 mod n
- M: 消息空间 M ∈ Z P ∗ M\in Z^*_{P} M∈ZP∗
- S: 签名空间 Z P ∗ × Z P ∗ Z_P^*\times Z_{P}^* ZP∗×ZP∗
- h,n是公钥,k是密钥
签名过程
- 选随机数r满足(r, n) = 1
- 计算 s 1 = ( M / r + r ) / 2 m o d n s_1 =(M/r + r)/2\ mod\ n s1=(M/r+r)/2 mod n
- 计算 s 2 = k ( M / r − r ) / 2 m o d n s_2 =k(M/r - r)/2\ mod\ n s2=k(M/r−r)/2 mod n
- S i g k ( M , k ) = S = ( s 1 , s 2 ) Sig_k(M,k) = S = (s_1,s_2) Sigk(M,k)=S=(s1,s2)
验证过程
- 收到M和 ( s 1 , s 2 ) (s_1,s_2) (s1,s2)
- 计算 M ′ = s 1 2 + h × s + 2 2 m o d n M^{'} = s_1^2+h\times s+2^2\ mod\ n M′=s12+h×s+22 mod n
- 验证 V e r k ( H ( M ) , r , s ) = t r u e ⇔ M = M ′ Ver_k(H(M), r, s) = true \Leftrightarrow M = M^{'} Verk(H(M),r,s)=true⇔M=M′
缺陷:
对于二次,三次多项式构造的签名并不安全
四次多项式已被拱北
ESIGN在OSS上提出的新方案
离散对数
- p: 大素数
- q: (p-1)的素因子
- g: g ∈ Z P ∗ ∧ g q = 1 m o d p g\in Z_P^* \land g^q=1\ mod\ p g∈ZP∗∧gq=1 mod p
- M: 消息空间 M ∈ Z P ∗ M\in Z^*_{P} M∈ZP∗
- S: 签名空间
- x: 用户密钥, 1 < x < q 1< x<q 1<x<q
- y:用户公钥 y = g x m o d p y = g^x\ mod\ p y=gx mod p
p,q,g,y公钥,x密钥
签名过程
- 选择随机数k, 0 < k < q 0<k<q 0<k<q
- 计算H(m)
- 计算 r = g k m o d p r = g^k\ mod\ p r=gk mod p
- 签字 a k = b + c x m o d q ak = b + cx\ mod\ q ak=b+cx mod q
- S i g k ( m ) = ( r , s ) Sig_k(m) = (r,s) Sigk(m)=(r,s)作为签名,将m和(r,s)送给对方
验证
- 收到m和(r,s)
- V e r ( M , r , s ) = t r u e ⇔ r a = g b y c m o d q Ver(M,r,s) = true \Leftrightarrow r^a=g^by^c\ mod\ q Ver(M,r,s)=true⇔ra=gbyc mod q
以上签名可以看作其特例
| a | b | c | 对应体制 |
|---|---|---|---|
| ± r ± r ±r | ± s ±s ±s | ± H ( m ) ±H(m) ±H(m) | Yen; Laih |
| ± r ± r ±r | ± H ( m ) ±H(m) ±H(m) | ± s ±s ±s | Agnew; Yen |
| ± s ±s ±s | ± r ± r ±r | ± H ( m ) ±H(m) ±H(m) | |
| ± s ±s ±s | ± H ( m ) ±H(m) ±H(m) | ± r ± r ±r | ElGamal; DSA |
| ± H ( m ) ±H(m) ±H(m) | ± s ±s ±s | ± r ± r ±r | Schonorr; Nyberg |
| ± H ( m ) ±H(m) ±H(m) | ± r ± r ±r | ± s ±s ±s |
11. 其他签名
- 不可否认签名
- 防失败签名 fail-stop signature
- 盲签名 blind signature
- 群签名 group signature (代表一个群体,匿名)
- 代理签名 proxy
- 指定证实人签名 designate confirmer signature
- 一次性签名 one time
消息认证码MAC基本用途
- 消息认证
- 消息认证与保密:计算MAC后加密
- 消息认证与保密:先加密后计算MAC
与杂凑算法/加密/签名结合方案
- 保密性 + 消息认证
- 仅消息认证
- 即消息认证,也有数字签名
- 提供保密性,消息认证,数字签名