SHA
Hash函数
定义
-
任意长度的数据M变换为定长码h
h = H A S H ( M ) h = H ( M ) h = HASH(M)\quad h = H(M) h=HASH(M)h=H(M) -
实用性: 给定M,计算h时高效的
-
安全性:
- 单向性 给出h,反向计算原文x时不可行的,否则截取H(M||Key),hash逆运算可以得到Key泄漏密钥
- 抗碰撞性,给定x,找到KaTeX parse error: Undefined control sequence: \noteq at position 2: y\̲n̲o̲t̲e̲q̲ ̲x,使得 H ( y ) = H ( x ) H(y)=H(x) H(y)=H(x)是不可行的。 否则可以冒充
- 抗强碰撞性 找到任何满足 H ( x ) = H ( y ) H(x)=H(y) H(x)=H(y)的偶对 ( x , y ) (x,y) (x,y)在计算上是不可行的
hash函数一般结构
- 将输入分为L-1个大小为b位的分组
- 若第L-1个分组不足b位,填充到b位
- 附加第L个分组,表示总长度
(输入中包含长度,所以攻击者必须找出具 所以攻击者必须找出具 有相同Hash值且长度相等的两条报文 OR 长度不等,加入报文长度后hash相同的报文)
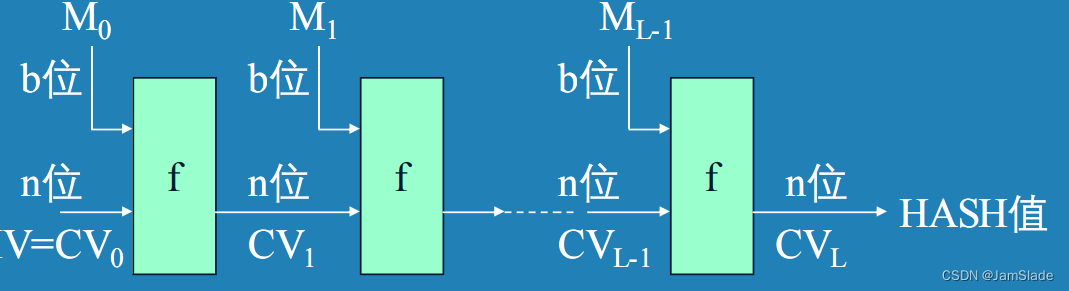
b位分组通过L次连接迭代通过压缩函数f,f输出n位
作用
- 错误检测
- 作为MAC,用于认证
- 数字签名
- 保密
SHA-1 HASH函数
SHA-0, 1, 2三种
SHA-2包括三个hash函数, SHA-256, SHA-384, SHA-512
SHA-1基础: MD5
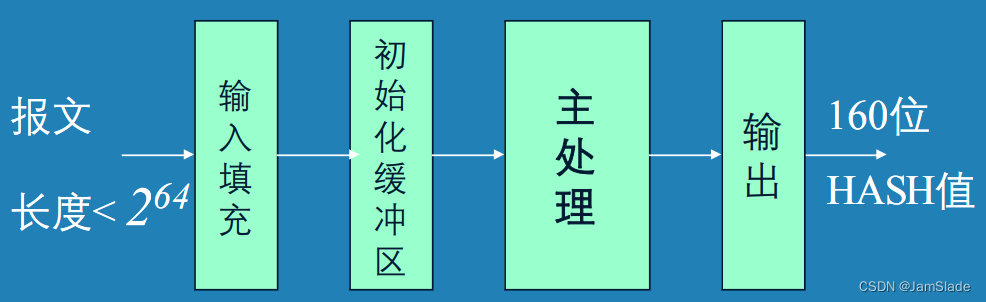
SHA-1输入长度,小于
2
6
4
2^64
264位的报文,输出
160
160
160位报文摘要
对输入按 512位分组
运算算法
- 输入填充,让填充后的报文长度满足
l e n g t h = 448 m o d 512 length = 448 \ mod \ 512 length=448 mod 512
- 在末尾加一个1和若干个0
- 本身已满足的话,为了避免二义性,添加512位(填充数介于1-512)
- 初始化缓冲区
- 缓冲区:5个32位寄存器,保存160位的中间 or 最终结果
- 五个寄存器初始化如下:
A: 67452301
B: EFCDAB89
C: 98BADCFE
D: 10325476
E: C3D2E1F0
(大端模式存储)
- 主处理
- 每次处理512位分组,循环次数 – L
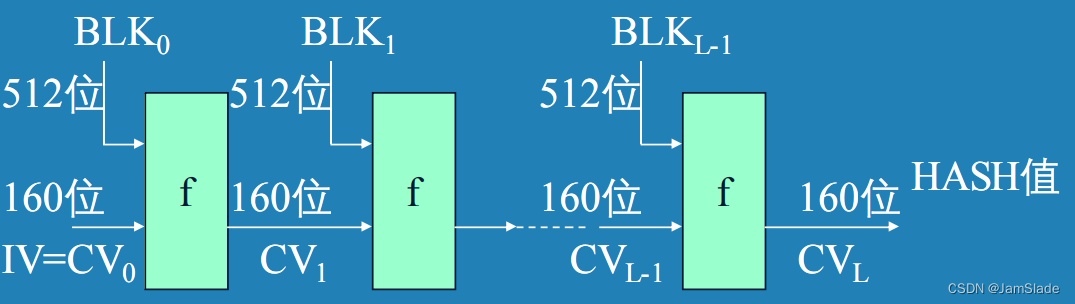
- f压缩函数位核心
- 四层运算(每层20步迭代)组成, 四层运算结构相同
- 输入当前要处理的是512位的分组BLK和160位缓冲区ABCDE的内容
- 每层要对ABCDE内容更新(逻辑函数f是不一样的)
- 第四层输出与第一层输出相加得到最后结果
- 输出
- 所有的L个512位的分组处理完后,第L个分组的输出即是160位的报文摘要
- 归纳
C V 0 = I V CV_0 = IV CV0=IV
KaTeX parse error: Undefined control sequence: \leL at position 29: …_i\quad 0\le i \̲l̲e̲L̲ ̲- 1
具体如下
C
V
i
+
1
(
0
)
=
C
V
i
(
0
)
+
A
i
C
V
i
+
1
(
1
)
=
C
V
i
(
1
)
+
B
i
C
V
i
+
1
(
2
)
=
C
V
i
(
2
)
+
C
i
C
V
i
+
1
(
3
)
=
C
V
i
(
3
)
+
D
i
C
V
i
+
1
(
4
)
=
C
V
i
(
4
)
+
E
i
CV_{i+1}(0) = CV_i(0)+A_i \\ CV_{i+1}(1) = CV_i(1)+B_i \\ CV_{i+1}(2) = CV_i(2)+C_i \\ CV_{i+1}(3) = CV_i(3)+D_i \\ CV_{i+1}(4) = CV_i(4)+E_i
CVi+1(0)=CVi(0)+AiCVi+1(1)=CVi(1)+BiCVi+1(2)=CVi(2)+CiCVi+1(3)=CVi(3)+DiCVi+1(4)=CVi(4)+Ei
上述的+是 mod 2^{32}加法
- 压缩函数
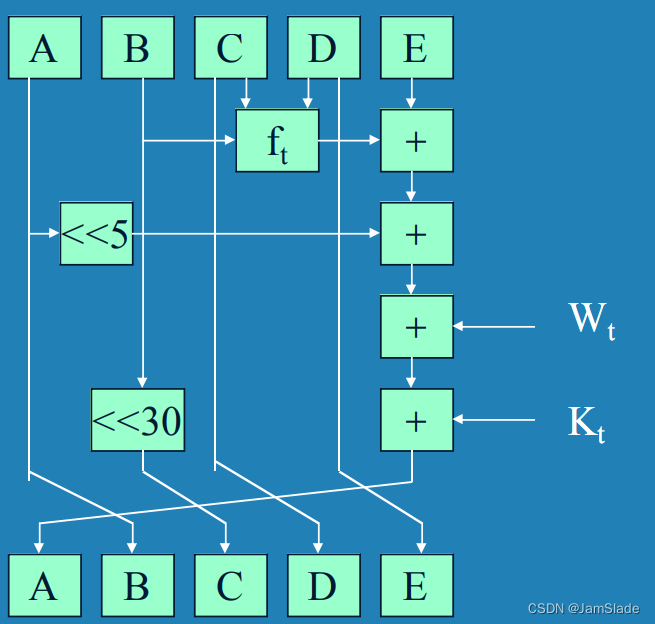
缺点
- 输出B=输入A
- 输出D=输入C
- 输出E=输入D
- A、C、D没有运算
形式
A
←
(
E
+
f
t
(
B
,
C
,
D
)
+
(
A
<
<
5
)
+
W
t
+
K
t
)
B
←
A
C
←
B
<
<
30
D
←
C
E
←
A \leftarrow (E + f_t(B,C,D) + (A<<5) + W_t + K_t) \\ B\leftarrow A\\ C\leftarrow B<<30\\ D\leftarrow C\\E\leftarrow
A←(E+ft(B,C,D)+(A<<5)+Wt+Kt)B←AC←B<<30D←CE←
- 单轮对A,B,C,D,E进行20次迭代, 四轮共80次迭代 0 ≤ t ≤ 79 0\le t \le 79 0≤t≤79
- < < s <<s <<s表示32位变量左移s位
- + + +为 mod 32的加法
- 逻辑函数
f
t
f_t
ft四个轮次略有区别
- f 1 = f t ( B , C , D ) = ( B ∧ C ) ∨ ( ¬ B ∧ D ) f_1=f_t(B,C,D) = (B\land C)\lor(\lnot B\land D) f1=ft(B,C,D)=(B∧C)∨(¬B∧D)
- f 2 = f t ( B , C , D ) = B ⊕ C ⊕ D f_2 = f_t(B,C,D) = B\oplus C\oplus D f2=ft(B,C,D)=B⊕C⊕D
- f 3 = f t ( B , C , D ) = ( B ∧ C ) ∨ ( B ∧ D ) ∨ ( C ∧ D ) f_3=f_t(B,C,D) = (B\land C)\lor(B\land D) \lor(C\land D) f3=ft(B,C,D)=(B∧C)∨(B∧D)∨(C∧D)
-
f
4
=
f
t
(
B
,
C
,
D
)
=
B
⊕
C
⊕
D
f_4 = f_t(B,C,D) = B\oplus C\oplus D
f4=ft(B,C,D)=B⊕C⊕D
- 缺点: f 2 f 4 f_2\ f_4 f2 f4均为线性函数
-
K
t
K_t
Kt 加法常量,共有四个不同加法产量
- 第一层 5A827999
- 第二层 6ED9EBA1
- 第三次 8F1BBCDC
- 第四层 CA62C1D6
- 缺点: 压缩字K作用范围太小,只影响A不影响B\C\D\E
-
W
t
W_t
Wt:当前分组BLK导出的32位字
- 每步使用从512位的报文分组BLK导出的一个32位的字 W t W_t Wt
- 把BLK划分为16个32位的字( M 0 , M 15 M_0, M_{15} M0,M15),扩展到80个32位字( M 0 , M 79 M_0, M_{79} M0,M79)
- 0 ≤ t ≤ 15 W t = M t 0\le t\le 15\quad W_t = M_t 0≤t≤15Wt=Mt
-
16
≤
t
≤
79
W
t
=
(
W
t
−
16
⊕
W
t
−
13
⊕
W
t
−
8
⊕
W
t
−
3
)
<
<
1
16\le t \le 79\quad W_t = (W_{t-16}\oplus W_{t-13}\oplus W_{t-8}\oplus W_{t-3})<<1
16≤t≤79Wt=(Wt−16⊕Wt−13⊕Wt−8⊕Wt−3)<<1
- 缺点: 压缩函数是线性函数; 压缩字 W t W_t Wt的作用范围太小(和K一样)
补充
- SHA-1可用
- MD-5不安全
SHA-2 HASH函数
- 三个Hash函数 SHA-256/384/512
- AES配套
- 安全性能更强
- 与SHA-1比较:结构相同、逻辑函数相同、mod运算相同
| (单位:bit) | SHA-1 | SHA-256 | SHA-384 | SHA-512 |
|---|---|---|---|---|
| 消息摘要长度 | 160 | 256 | 384 | 512 |
| 消息长度 | <2^64 | <2^64 | <2^128 | <2^128 |
| 分组长度 | 512 | 512 | 1024 | 1024 |
| 字长度 | 32 | 32 | 64 | 64 |
| 步骤数 | 80 | 64 | 80 | 80 |
| 安全性 | 80 | 128 | 192 | 25 |
安全性:对输出长度为n比特的hash函数的攻击产生碰撞的工具约为 2 n / 2 2^{n/2} 2n/2
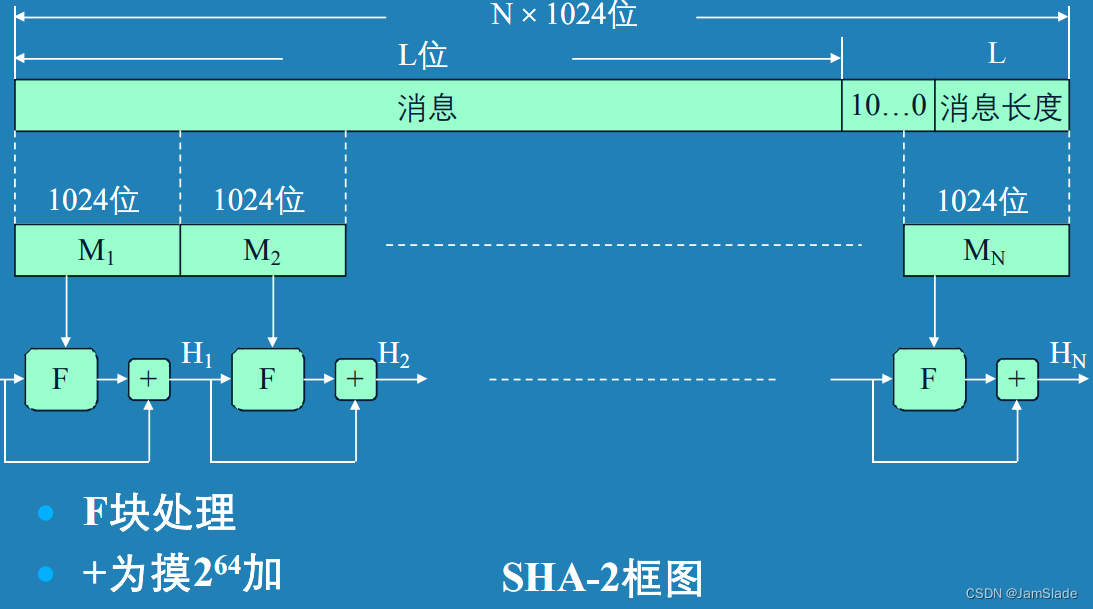
SHA-512
- 输入长度 < 2 128 <2^{128} <2128
- 数据分组长度 1024
- 输出长度 512
运算算法
- 填充
- 使填充后的长度=896 mod 1024
- 已满足也需要填充(1个1 若干个0)
- 附加长度
- 填充后附加128位的块,表示原消息长度
完成1、2步后,数据长度为1024的整数倍, 数据 / 1024为块数N,对其迭代处理
- 初始化缓冲区
- 中间结果、最终结果存于512比特的缓冲区中,缓冲区使用8个64比特的寄存器(A,B,C,D,E,F,G,H)
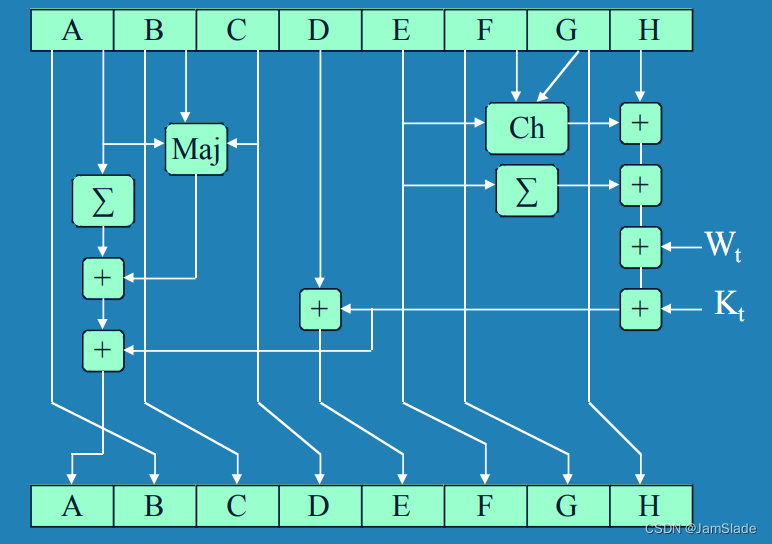
A = 6 A 09 E 667 F 3 B C C 908 E = 510 E 527 F A D E 682 D 1 B = B B 67 A E 8584 C A A 73 B F = 9 B 05688 C 2 B 3 E 6 C 1 F C = 3 C 6 E F 372 F E 94 F 82 B G = 1 F 83 D 9 A B F B 41 B D 6 B D = A 54 F F 53 A 5 F 1 D 36 F 1 H = 5 B E 0 C D 19137 E 2179 A=6A09E667F3BCC908 \quad E=510E527FADE682D1 \\ B=BB67AE8584CAA73B \quad F=9B05688C2B3E6C1F \\ C=3C6EF372FE94F82B \quad G=1F83D9ABFB41BD6B\\ D=A54FF53A5F1D36F1 \quad H=5BE0CD19137E2179 A=6A09E667F3BCC908E=510E527FADE682D1B=BB67AE8584CAA73BF=9B05688C2B3E6C1FC=3C6EF372FE94F82BG=1F83D9ABFB41BD6BD=A54FF53A5F1D36F1H=5BE0CD19137E2179
来源:前八个素数平方根,取小数部分前64个比特
存储方式:高有效字节存低字节位置(大端
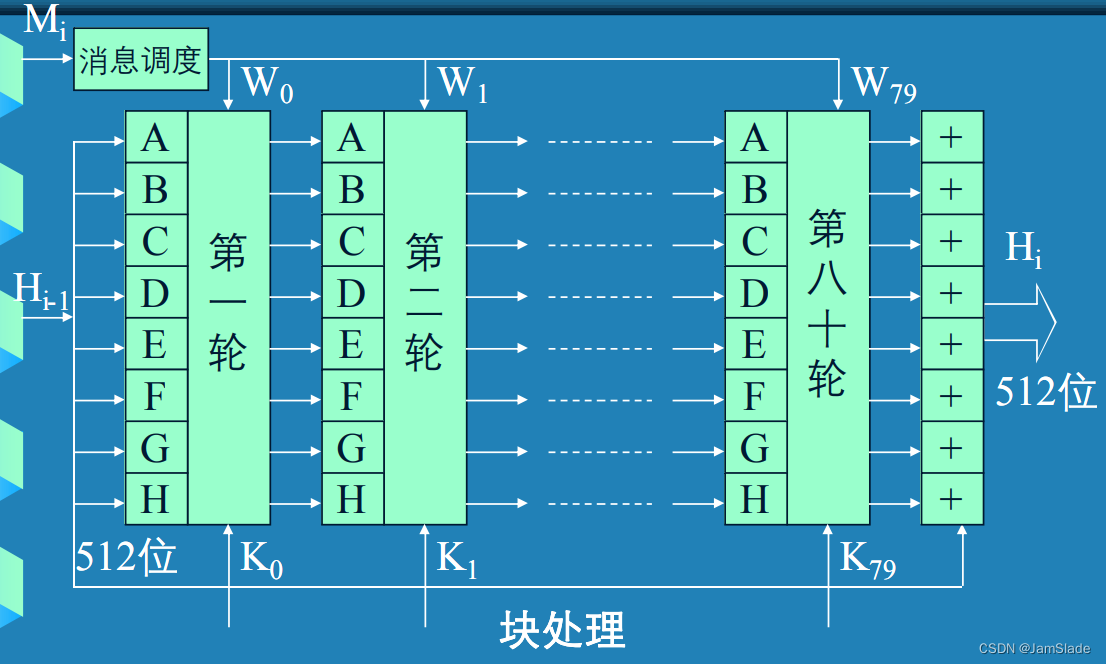
- 块处理
1024比特快的处理 + 80轮迭代运算
- 512bits缓冲区的ABCDEFGH为输入,更新缓冲区的值。第一轮时,缓冲区里的值是中间 缓冲区里的值是中间的Hash值 H i − 1 H_{i-1} Hi−1
- 每轮t使用64bit的 W t W_t Wt与常数 K t K_t Kt
- 迭代后输出 H i H_i Hi
- 存储方式:高有效字节存于低地址字节位置
- 轮函数
前两个同SHA-1,后两函数不同
C
H
(
E
,
F
,
G
)
=
(
E
∧
F
)
⊕
(
¬
E
∧
G
)
M
a
j
(
A
,
B
,
C
)
=
(
A
∧
B
)
⊕
(
A
∧
C
)
⊕
(
B
∧
C
)
∑
0
512
=
R
O
T
R
28
(
A
)
⊕
R
O
T
R
34
(
A
)
⊕
R
O
T
R
39
(
A
)
∑
1
512
=
R
O
T
R
14
(
E
)
⊕
R
O
T
R
18
(
E
)
⊕
R
O
T
R
41
(
E
)
CH(E,F,G)=(E \land F)⊕(\lnot E \land G)\\ Maj(A,B,C)=(A \land B)⊕(A \land C)⊕(B \land C)\\ ∑_0^{512}=ROTR^{28}(A)⊕ ROTR^{34}(A)⊕ ROTR^{39}(A)\\ ∑_1^{512}=ROTR^{14}(E)⊕ ROTR^{18}(E)⊕ ROTR^{41}(E)
CH(E,F,G)=(E∧F)⊕(¬E∧G)Maj(A,B,C)=(A∧B)⊕(A∧C)⊕(B∧C)0∑512=ROTR28(A)⊕ROTR34(A)⊕ROTR39(A)1∑512=ROTR14(E)⊕ROTR18(E)⊕ROTR41(E)
- R O T R i ( X ) ROTR^i(X) ROTRi(X)表示X循环右移i位
- 附加常数
K
t
K_t
Kt
- 最小的80个素数开立方,取根的小数部分前64bit
- 小数部分随机,消除数据中的规律性
- 压缩字
W
t
W_t
Wt
- 1024bit的块中取出,分为16个64位的 M t M_t Mt
- W t = M t 0 ≤ t ≤ 15 W_t = M_t\quad 0\le t\le 15 Wt=Mt0≤t≤15
- W t = σ 1 512 ( W t − 2 ) + W t − 7 + σ 0 512 ( W t − 15 ) + W t − 16 W_t = \sigma_1^{512}(W_{t-2})+W_{t-7} + \sigma_0^{512}(W_{t-15}) + W_{t-16} Wt=σ1512(Wt−2)+Wt−7+σ0512(Wt−15)+Wt−16
- σ 0 512 ( x ) = R O T R 1 ( x ) ⊕ R T O R 8 ( x ) ⊕ S H R 7 ( x ) \sigma_0^{512}(x) = ROTR^1(x) \oplus RTOR^8(x) \oplus SHR^7(x) σ0512(x)=ROTR1(x)⊕RTOR8(x)⊕SHR7(x)
- σ 1 512 ( x ) = R O T R 19 ( x ) ⊕ R T O R 61 ( x ) ⊕ S H R 6 \sigma_1^{512}(x) = ROTR^{19}(x) \oplus RTOR^{61}(x) \oplus SHR^6 σ1512(x)=ROTR19(x)⊕RTOR61(x)⊕SHR6
- S H R i ( x ) 表示 x 左移 i 位右边填 0 SHR^i(x)表示x左移i位右边填0 SHRi(x)表示x左移i位右边填0
函数变化
T
1
=
H
+
C
h
(
E
,
F
,
G
)
+
(
Σ
1
5
12
E
)
+
W
t
+
K
t
T
2
=
(
Σ
0
512
A
)
+
M
a
j
(
A
,
B
,
C
)
A
=
T
1
+
T
2
B
=
A
C
=
B
D
=
C
E
=
D
+
T
1
F
=
E
G
=
F
H
=
G
T_1 = H + Ch(E,F,G) + (\Sigma_1^512 E) + W_t + K_t\\ T_2 = (\Sigma ^{512}_0 A) + Maj(A,B,C)\\ A = T_1 + T_2\\ B = A\\ C = B\\ D = C\\ E = D+T_1\\ F = E\\ G = F\\ H = G
T1=H+Ch(E,F,G)+(Σ1512E)+Wt+KtT2=(Σ0512A)+Maj(A,B,C)A=T1+T2B=AC=BD=CE=D+T1F=EG=FH=G
缺点:直接相等的太多
总结
- SHA-512结构等同SHA-1
- 前者输出长度更长,抗穷举攻击能力更强
- 逻辑函数与后者差别不大 (SHA-1 20轮使用一个逻辑函数、 SHA-2 每轮4个逻辑函数)
- 应用未开始、安全性暂时未检验