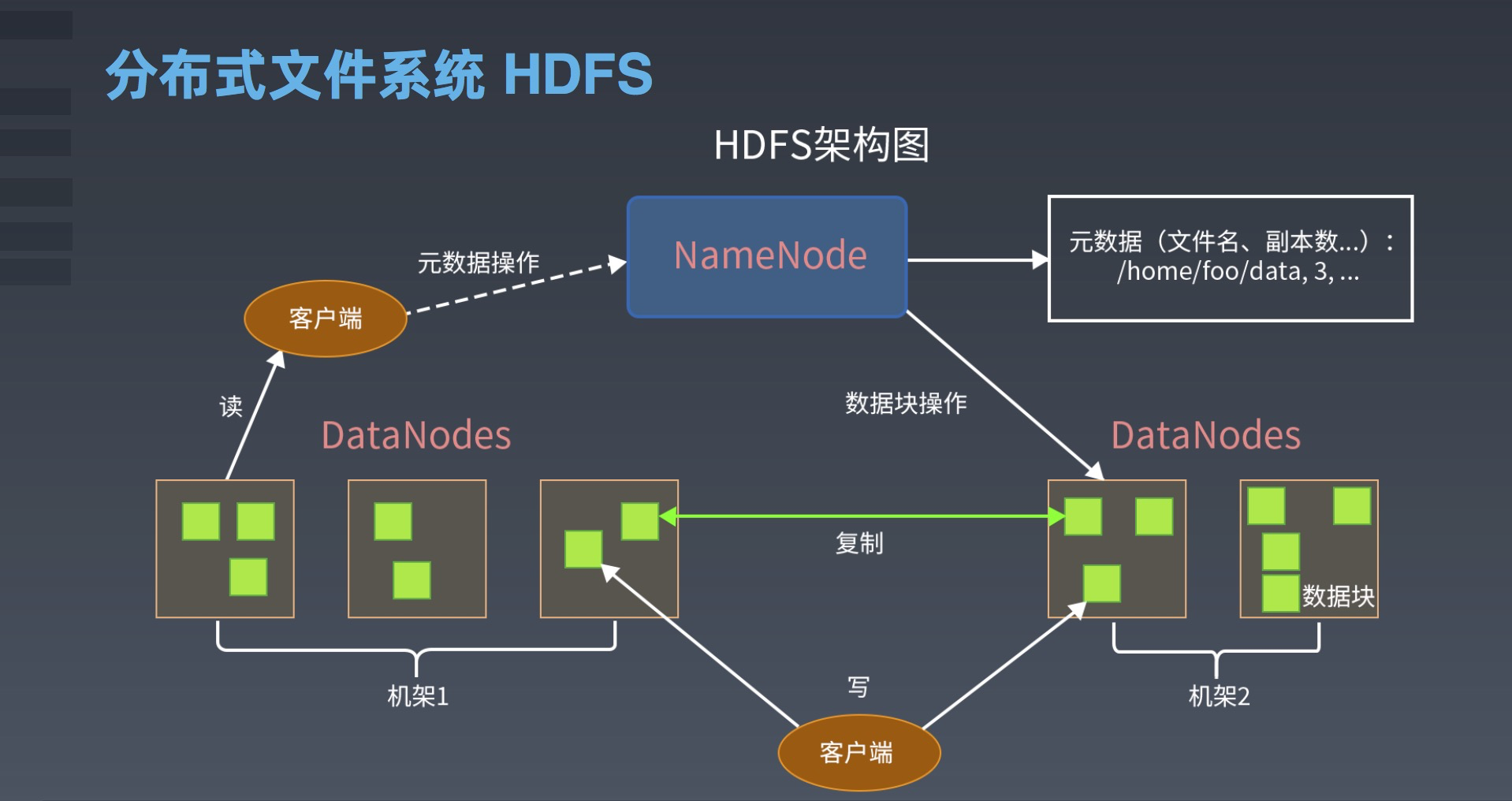
树和二叉树
文章目录
- 树和二叉树
- 树
- 定义
- 形式化定义
- 递归定义
- 树的(逻辑)表示
- 树形表示法
- 文氏图表示法
- 凹入表示法
- 括号表示法
- 树的基本术语
- 1. 结点的度与树的度
- 2. 分支结点与叶结点
- 3. 路径与路径长度
- 4. 孩子结点、双亲结点和兄弟结点
- 5. 子孙结点和祖先结点
- 6. 结点的层次和树的高度
- 7. 有序树和无序树
- 8. 森林
- 树的性质
- 性质1:树中的结点数等于所有结点的度数之和加1。
- 度为m的树的其他重要特性
- 性质2:度为m的树中第i层至多有mi-1个结点(i>=1)。
- 性质3:高度为h的m叉树至多有(mh-1)/(m-1)个结点。
- 性质4:具有n个结点的m叉树的最小高度为⌈logm(n(m-1)+1)⌉。
- 树的基本运算
- 树的遍历
- 树的先根遍历
- 树的后根遍历
- 树的层次遍历
- 树的存储结构
- 1. 双亲存储结构
- 2. 孩子链式存储结构
- 3. 孩子兄弟链存储结构
- 二叉树
- 递归定义
- 二叉树的五种基本形态
- 逻辑结构表示法
- 二叉树和二次树的区别
- 两种特殊的二叉树(满二叉树和完全二叉树)
- 满二叉树
- 完全二叉树
- 完全二叉树的特点
- 二叉树的性质
- 性质1
- 性质2
- 性质3
- 性质4:(完全二叉树的性质)
- 森林、树转换为二叉树
- 二叉树还原为森林、树
- 二叉树的存储结构
- 二叉树的顺序存储结构
- 完全二叉树的顺序存储结构
- 一般二叉树的顺序存储结构
- 二叉树的顺序存储结构的特点
- 二叉树的链式存储结构
- 二叉链存储结构示例
- 二叉链存储结构的特点
- 求二叉链的空指针个数
- 二叉树的基本运算
- 创建二叉树
- 销毁二叉树
- 查找结点
- 找孩子结点
- 求高度
- 输出二叉树
树
定义
形式化定义

递归定义

树的(逻辑)表示
树形表示法

文氏图表示法

凹入表示法

括号表示法

树的基本术语
- 树结点 (Tree Node) :树中元素的基本单位。包含一个数据元素及若干指向其子树的分支。
- 结点的度 (Degree) :结点拥有的子树个数。
- 树的度 (Tree Degree) :树中各结点的度的最大值。
- 双亲 (Parent)和孩子 (Child) :把一个树结点的直接前驱 (只有一个)称为该结点的双亲;相反的,把一个树结点的所有直接后继 (零到多个)称为该结点的孩子。
- 兄弟 (Sibling) :同一双亲的孩子之间称为兄弟。
- 祖先 (Ancenstor):从根到该结点所经分支上的所有结点。
- 子孙 (Descendant) :以某结点为根的子树中的任一结点。
- 树的层次 (Level) :从根结点算起,根为第一层,根的孩子为第二层,以此类推。
- 树的深度 (Depth)或高度:树中各结点层次的最大值。
- 有序树 (Ordered Tree)和无序树 ((Unordered Tree)) :如果树中结点的各子树可看成从左至右是有次序的 (即不能互换),则称该树为有序树,否则称为无序树。
1. 结点的度与树的度

2. 分支结点与叶结点

3. 路径与路径长度

4. 孩子结点、双亲结点和兄弟结点

5. 子孙结点和祖先结点

6. 结点的层次和树的高度

7. 有序树和无序树

8. 森林


树的性质
性质1:树中的结点数等于所有结点的度数之和加1。


度为m的树的其他重要特性


小练一下

性质2:度为m的树中第i层至多有mi-1个结点(i>=1)。

性质3:高度为h的m叉树至多有(mh-1)/(m-1)个结点。

等比数列前N项和计算公式:Sn =a1 (1-q^n)/ (1-q)
性质4:具有n个结点的m叉树的最小高度为⌈logm(n(m-1)+1)⌉。


树的基本运算
树的运算主要分为三大类:
查找满足某种特定关系的结点,如查找当前结点的双亲结点等。插入或删除某个结点,如在树的当前结点上插入一个新结点或删除当前结点的第i个孩子结点等。遍历树中每个结点。
树的遍历

树的先根遍历

树的后根遍历

树的层次遍历

树的存储结构
1. 双亲存储结构


typedef struct {
int data;
int parent;
}PTree[MaxSize];
优缺点
双亲存储结构的优点是可以方便地找到任意结点的双亲结点,但是缺点是不容易找到任意结点的孩子结点,也不方便计算树的深度和度数。
2. 孩子链式存储结构


优缺点
孩子链式存储结构的优点是可以方便地找到任意结点的所有孩子结点,但是缺点是不容易找到任意结点的双亲结点,也不方便计算树的深度和度数。
定义MaxSize为3,然后定义TSonNode类型,如下:
#define MaxSize 3
typedef struct node{
int data;
struct node *sons[MaxSize];
} TSonNode;
然后,创建10个TSonNode类型的结点,并给它们赋值,如下:
//创建10个结点
TSonNode *nodes[10];
for(int i = 0; i < 10; i++){
//为每个结点分配内存空间
nodes[i] = (TSonNode *)malloc(sizeof(TSonNode));
//为每个结点的data赋值
nodes[i]->data = i;
//为每个结点的sons数组赋初值NULL
for(int j = 0; j < MaxSize; j++){
nodes[i]->sons[j] = NULL;
}
}
接下来,建立结点之间的关系,即设置sons数组的指针,如下:
//建立结点之间的关系
nodes[0]->sons[0] = nodes[1]; //节点0的第一个孩子是节点1
nodes[0]->sons[1] = nodes[2]; //节点0的第二个孩子是节点2
nodes[1]->sons[0] = nodes[3]; //节点1的第一个孩子是节点3
nodes[1]->sons[1] = nodes[4]; //节点1的第二个孩子是节点4
nodes[2]->sons[0] = nodes[5]; //节点2的第一个孩子是节点5
nodes[2]->sons[1] = nodes[6]; //节点2的第二个孩子是节点6
nodes[3]->sons[0] = nodes[7]; //节点3的第一个孩子是节点7
nodes[4]->sons[0] = nodes[8]; //节点4的第一个孩子是节点8
nodes[6]->sons[0] = nodes[9]; //节点6的第一个孩子是节点9
最后,遍历这棵树,打印出每个结点的数据和孩子结点的数据,如下:
//遍历这棵树,打印出每个结点的数据和孩子结点的数据
for(int i = 0; i < 10; i++){
printf("node %d: data = %d, sons = ", i, nodes[i]->data);
for(int j = 0; j < MaxSize; j++){
if(nodes[i]->sons[j] != NULL){
printf("%d ", nodes[i]->sons[j]->data);
}
else{
printf("NULL ");
}
}
printf("\n");
}
运行这段代码,可以得到以下输出:
node 0: data = 0, sons = 1 2 NULL
node 1: data = 1, sons = 3 4 NULL
node 2: data = 2, sons = 5 6 NULL
node 3: data = 3, sons = 7 NULL NULL
node 4: data = 4, sons = 8 NULL NULL
node 5: data = 5, sons = NULL NULL NULL
node 6: data = 6, sons = 9 NULL NULL
node 7: data = 7, sons = NULL NULL NULL
node 8: data = 8, sons = NULL NULL NULL
node 9: data = 9, sons = NULL NULL NULL
3. 孩子兄弟链存储结构



优缺点
孩子兄弟链存储结构的优点是可以将任意一棵树转化为一棵二叉树,从而利用二叉树的算法和性质,也可以方便地找到任意结点的孩子结点和兄弟结点,但是缺点是不容易找到任意结点的双亲结点,也不方便计算树的深度和度数。
首先,定义TSBNode类型,如下:
typedef struct tnode{
int data;
struct tnode *hp;
struct tnode *vp;
} TSBNode;
然后,创建9个TSBNode类型的结点,并给它们赋值,如下:
//创建9个结点
TSBNode *nodes[9];
for(int i = 0; i < 9; i++){
//为每个结点分配内存空间
nodes[i] = (TSBNode *)malloc(sizeof(TSBNode));
//为每个结点的data赋值
nodes[i]->data = i;
//为每个结点的hp和vp赋初值NULL
nodes[i]->hp = NULL;
nodes[i]->vp = NULL;
}
接下来,建立结点之间的关系,即设置hp和vp指针,如下:
//建立结点之间的关系
nodes[0]->vp = nodes[1]; //节点0的第一个孩子是节点1
nodes[1]->hp = nodes[2]; //节点1的水平方向的下一个兄弟是节点2
nodes[1]->vp = nodes[3]; //节点1的第一个孩子是节点3
nodes[2]->hp = nodes[4]; //节点2的水平方向的下一个兄弟是节点4
nodes[2]->vp = nodes[5]; //节点2的第一个孩子是节点5
nodes[3]->hp = nodes[6]; //节点3的水平方向的下一个兄弟是节点6
nodes[4]->vp = nodes[7]; //节点4的第一个孩子是节点7
nodes[6]->hp = nodes[8]; //节点6的水平方向的下一个兄弟是节点8
最后,遍历这棵树形表,打印出每个结点的数据和水平方向和垂直方向的下一个结点的数据,如下:
//遍历这棵树形表,打印出每个结点的数据和水平方向和垂直方向的下一个结点的数据
for(int i = 0; i < 9; i++){
printf("node %d: data = %d, hp = ", i, nodes[i]->data);
if(nodes[i]->hp != NULL){
printf("%d ", nodes[i]->hp->data);
}
else{
printf("NULL ");
}
printf(", vp = ");
if(nodes[i]->vp != NULL){
printf("%d ", nodes[i]->vp->data);
}
else{
printf("NULL ");
}
printf("\n");
}
运行这段代码,可以得到以下输出:
node 0: data = 0, hp = NULL , vp = 1
node 1: data = 1, hp = 2 , vp = 3
node 2: data = 2, hp = 4 , vp = 5
node 3: data = 3, hp = 6 , vp = NULL
node 4: data = 4, hp = NULL , vp = 7
node 5: data = 5, hp = NULL , vp = NULL
node 6: data = 6, hp = 8 , vp = NULL
node 7: data = 7, hp = NULL , vp = NULL
node 8: data = 8, hp = NULL , vp = NULL
二叉树
递归定义

例子

二叉树的五种基本形态

逻辑结构表示法

二叉树和二次树的区别

两种特殊的二叉树(满二叉树和完全二叉树)
满二叉树


完全二叉树

完全二叉树的特点

例题

二叉树的性质
性质1

求解一般二叉树结点个数方法归纳

性质2
性质3

性质4:(完全二叉树的性质)


求解完全二叉树结点个数方法归纳

森林、树转换为二叉树



二叉树还原为森林、树



二叉树的存储结构
二叉树的顺序存储结构

完全二叉树的顺序存储结构

一般二叉树的顺序存储结构

二叉树的顺序存储结构的特点


二叉树的链式存储结构

typedef struct btNode{
char data;
struct btNode *lChild, *rChild;
} BTNode, *BTree;
二叉链存储结构示例

二叉链存储结构的特点

求二叉链的空指针个数

二叉树的基本运算


创建二叉树
// 创建一个二叉树节点
BTree createNode(char data) {
BTree node = (BTree)malloc(sizeof(BTNode));
node->data = data;
node->lChild = NULL;
node->rChild = NULL;
return node;
}
// 创建一个二叉树
BTree createTree() {
char data;
scanf("%s", &data); // 输入节点数据
if (data == '#') { // 如果是'#',表示空节点,返回NULL
return NULL;
}
BTree root = createNode(data); // 创建根节点
root->lChild = createTree(); // 递归创建左子树
root->rChild = createTree(); // 递归创建右子树
return root; // 返回根节点
}

销毁二叉树


查找结点
查找一个二叉树中的某个节点的一种方法是使用递归的方式,从根节点开始,比较节点的数据和要查找的数据,如果相等,就返回该节点,如果不相等,就分别在左子树和右子树中递归查找,如果找到了,就返回找到的节点,如果没有找到,就返回NULL。
// 查找一个二叉树中的某个节点
BTree searchNode(BTree root, char data) {
if (root == NULL) { // 如果根节点为空,返回NULL
return NULL;
}
if (root->data == data) { // 如果根节点的数据和要查找的数据相等,返回根节点
return root;
}
BTree left = searchNode(root->lChild, data); // 递归在左子树中查找
if (left != NULL) { // 如果在左子树中找到了,返回找到的节点
return left;
}
BTree right = searchNode(root->rChild, data); // 递归在右子树中查找
if (right != NULL) { // 如果在右子树中找到了,返回找到的节点
return right;
}
return NULL; // 如果都没有找到,返回NULL
}


找孩子结点
查找一个二叉树中的某个节点的孩子节点的一种方法是使用递归的方式,从根节点开始,比较节点的数据和要查找的数据,如果相等,就返回该节点的左孩子和右孩子,如果不相等,就分别在左子树和右子树中递归查找,如果找到了,就返回找到的节点的孩子节点,如果没有找到,就返回NULL。
// 查找一个二叉树中的某个节点的孩子节点
void searchChildren(BTree root, char data, BTree &leftChild, BTree &rightChild) {
if (root == NULL) { // 如果根节点为空,返回NULL
leftChild = NULL;
rightChild = NULL;
return;
}
if (root->data == data) { // 如果根节点的数据和要查找的数据相等,返回根节点的左孩子和右孩子
leftChild = root->lChild;
rightChild = root->rChild;
return;
}
searchChildren(root->lChild, data, leftChild, rightChild); // 递归在左子树中查找
if (leftChild != NULL || rightChild != NULL) { // 如果在左子树中找到了,返回
return;
}
searchChildren(root->rChild, data, leftChild, rightChild); // 递归在右子树中查找
}
求高度

// 定义一个max方法
int max(int a, int b) {
if (a > b) { // 如果a大于b,返回a
return a;
}
else { // 否则,返回b
return b;
}
}
// 求一个二叉树的高度
int getHeight(BTree root) {
if (root == NULL) { // 如果根节点为空,返回0
return 0;
}
int leftHeight = getHeight(root->lChild); // 递归求左子树的高度
int rightHeight = getHeight(root->rChild); // 递归求右子树的高度
return max(leftHeight, rightHeight) + 1; // 返回较大的高度加1
}
输出二叉树

// 用二叉树的括号表示来输出二叉树
void printTreeWithBrackets(BTree root) {
if (root == NULL) { // 如果根节点为空,不打印任何东西
return;
}
printf("%c", root->data); // 打印根节点的数据
printf("("); // 打印一个左括号
printTreeWithBrackets(root->lChild); // 递归输出左子树
printf(")"); // 打印一个右括号
printf(",");
printf("("); // 打印一个左括号
printTreeWithBrackets(root->rChild); // 递归输出右子树
printf(")"); // 打印一个右括号
}