一、理论部分
率失真理论:
在给定失真的前提下如何最大限度第去除冗余。
在视频编码中的率失真理论为在给定码率RT的前提下最大限度的减少视频信息的失真,用数学描述为第一个式子所示,其中m*为取得最小码率时的编码方式,S为编码方式的集合。

对于该有条件的优化问题,可以采用拉格朗日优化法解决,通过引入拉格朗日系数λ将约束性求最值问题转为非约束性求最值问题,如第二个式子所示。
编码工具集:
如分级预测、帧内预测、帧间预测、44变换、88变换等、UVCL熵编码、CABAC熵编码等,当编码工具集固定时,对于固定的信源来说,一个编码器必然有一个确定的可操作点X的集合,由于集合点的离散型,可以在这个集合中近似出曲线包络,其中最优的一条包络被称为率失真曲线理论值。当编解码中引入了新的工具时,率失真曲线理论值可能会向左下方移动。

对于给定的R,其失真最小的点在率失真曲线理论值曲线上,上述率失真优化的公式一即让选择到的可操作点尽可能贴近理论值曲线。
编码工具决定了RD曲线的形态,即对于给定的信源,其有可能的(R,D)点集合,然而在每次编码中只能选择一个(R,D)点,通过编码策略进行选择,即怎样利用编码工具:什么时候采用帧内编码,什么时候采用帧间编码,怎样分块等让选择到的(R,D)点贴近理论曲线,这个选择的过程即率失真优化。
由于引入了拉格朗日系数,不再给定码率RT,设D+λR=J,过(R,D)做一条斜率为λ的斜线,其于纵轴截距即为J,让J最小即让截距最小,此时让(R,D)逼近理论曲线的问题可转化为过(R,D)做一条斜率为λ的斜线,让其与y轴截距最小,通过数学推导可知,当该斜线于曲线相切时理论最小,寻找给(R,D)点的过程即HEVC中的率失真优化。
通过引入λ可以更方便地去权衡视频质量与码率的重要性,当λ设置较大时,为了让J更小,就需要控制R的大小,即更注重码率,当λ设置较小时,为了让J更小,就需要控制D的大小,即更注重视频质量。
二、HEVC中帧内预测中的RDO
率失真优化贯穿于视频编解码的整个阶段,这里以帧内预测为例:
在HM中,帧内预测分为三个步骤:模式粗选(rough mode decision,RMD)、最佳可能预测模式(most possible mode,MPM)和率失真优化(RDO)
RMD依次按照35种模式对当前PU进行预测,计算预测像素于原始像素的差,对差值进行阿达玛变换后求和,将最好的几个模式加入备选模式集中
MPM依据相邻PU间的相似性,将待编码PU附近的已编码PU的模式加入备选模式集中
RDO在最终的备选模式集中进行优化,选出最优编码策略,这个过程如下:
01.分层递归遍历所有CU划分
由于HEVC的编码结构为基于CTU的四叉树划分,这个过程的率失真优化流程可以按照如下递归式表式:
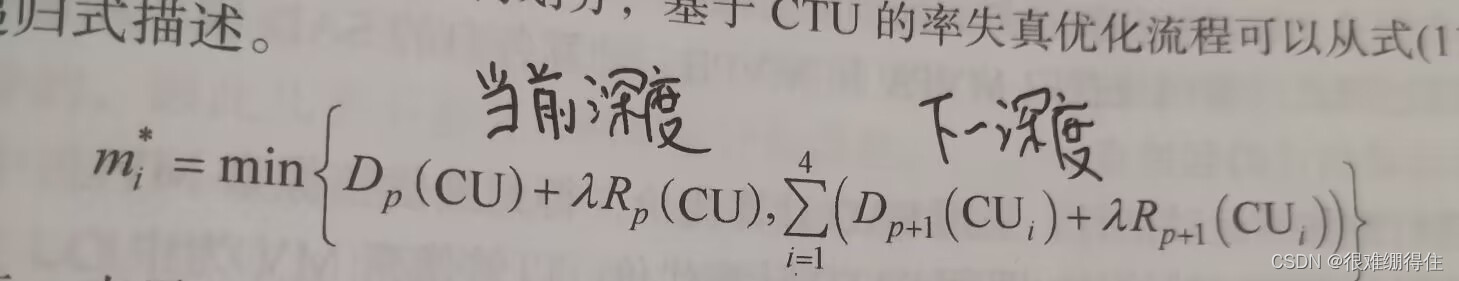
每次递归比较当前深度的率失真代价于下一深度的率失真代价
在递归的过程中确定出能使率失真代价最小的编码策略
02.对每个CU确定PU划分
03.对每个PU进行帧内预测
三、HM中的RDO实现
在TLibCommon中的TComCudata中存在三个成员函数:
Double& getTotalCost ( ) { return m_dTotalCost; }
Distortion& getTotalDistortion ( ) { return m_uiTotalDistortion; }
UInt& getTotalBits ( ) { return m_uiTotalBits; }
分别为获取总的率失真代价,计算总失真,计算总比特数,这些数据作为该类的成员,可以被其他函数修改,
如总失真m_dTotalCost在CTU的初始化时被设为最大值,在后续递归调用时会被更新为其他值,总失真被初始化为0,总码率被初始化为0:

在计算某层CU划分结果的总结果时,需要计算其划分的pccu中的数值

上述计算是对于整体结果的统计,对于每个部分的相关数据计算的代码在TLibCommon中的TComRDcost中:
如计算失真的代码如下:
Distortion TComRdCost::getDistPart( Int bitDepth, const Pel* piCur, Int iCurStride, const Pel* piOrg, Int iOrgStride, UInt uiBlkWidth, UInt uiBlkHeight, const ComponentID compID, DFunc eDFunc )
{
DistParam cDtParam;
setDistParam( uiBlkWidth, uiBlkHeight, eDFunc, cDtParam );
cDtParam.pOrg = piOrg;
cDtParam.pCur = piCur;
cDtParam.iStrideOrg = iOrgStride;
cDtParam.iStrideCur = iCurStride;
cDtParam.iStep = 1;
cDtParam.bApplyWeight = false;
cDtParam.compIdx = MAX_NUM_COMPONENT; // just for assert: to be sure it was set before use
cDtParam.bitDepth = bitDepth;
if (isChroma(compID))
{
return ((Distortion) (m_distortionWeight[compID] * cDtParam.DistFunc( &cDtParam )));
}
else
{
return cDtParam.DistFunc( &cDtParam );
}
其中DistParam cDtParam;是存在有关图像失真相关数据的对象,DistFunc为失真函数
enum ComponentID
{
COMPONENT_Y = 0,
COMPONENT_Cb = 1,
COMPONENT_Cr = 2,
MAX_NUM_COMPONENT = 3
};
由于亮度与色度的失真计算方式不同,需要通过枚举型数据compID进行判断:
通过直接调用熵编码类的getNumberOfWrittenBits()来计算码率:
rpcTempCU->getTotalBits() += m_pcEntropyCoder->getNumberOfWrittenBits(); // dQP bits
rpcTempCU->getTotalBins() += ((TEncBinCABAC *)((TEncSbac*)m_pcEntropyCoder->m_pcEntropyCoderIf)->getEncBinIf())->getBinsCoded();
rpcTempCU->getTotalCost() = m_pcRdCost->calcRdCost( rpcTempCU->getTotalBits(), rpcTempCU->getTotalDistortion() );
计算出的码率getTotalBits()与失真getTotalDistortion一起通过calcRdCost拿去计算总失真:
计算总失真的代码如下:
Double TComRdCost::calcRdCost( Double numBits, Double distortion, DFunc eDFunc )
{
Double lambda = 1.0;
switch ( eDFunc )
{
case DF_SSE:
assert(0);
break;
case DF_SAD:
lambda = m_dLambdaMotionSAD[0]; // 0 is valid, because for lossless blocks, the cost equation is modified to compensate.
break;
case DF_DEFAULT:
lambda = m_dLambda;
break;
case DF_SSE_FRAME:
lambda = m_dFrameLambda;
break;
default:
assert (0);
break;
}
if (eDFunc == DF_SAD)
{
if (m_costMode != COST_STANDARD_LOSSY)
{
return ((distortion * 65536.0) / lambda) + numBits; // all lossless costs would have uiDistortion=0, and therefore this cost function can be used.
}
else
{
return distortion + (((numBits * lambda) ) / 65536.0);
}
}
else
{
if (m_costMode != COST_STANDARD_LOSSY)
{
return (distortion / lambda) + numBits; // all lossless costs would have uiDistortion=0, and therefore this cost function can be used.
}
else
{
return distortion + (numBits * lambda);
}
}
}
eDFunc 代表了不同的损失函数,不同损失函数在率失真代价计算中使用的λ有所不同,随后根据不同的模式与不同的代价函数计算出失真。