文章目录
- 题目收藏
- 不含重复字符的最长子串
- 最长公共子串
- 剑指 Offer
- 剑指 Offer 05. 替换空格
- 剑指 Offer 03. 数组中重复的数字
- 剑指 Offer 04. 二维数组中的查找
- 剑指 Offer 09. 用两个栈实现队列
- 剑指 Offer 07. 重建二叉树
- 剑指 Offer 06. 从尾到头打印链表
- 剑指 Offer 11. 旋转数组的最小数字
- 剑指 Offer 12. 矩阵中的路径
- 剑指 Offer 27. 二叉树的镜像
- 剑指 Offer 28. 对称的二叉树
- 剑指 Offer 29. 顺时针打印矩阵
- 剑指 Offer 30. 包含min函数的栈
- 剑指 Offer 31. 栈的压入、弹出序列
- 剑指 Offer 32 - I. 从上到下打印二叉树
- 剑指 Offer 32 - II. 从上到下打印二叉树 II
- 剑指 Offer 33. 二叉搜索树的后序遍历序列
- 剑指 Offer 34. 二叉树中和为某一值的路径
- 剑指 Offer 15. 二进制中1的个数
- 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
- 22.链表中倒数第k个节点
- 剑指 Offer II 022. 链表中环的入口节点
- 剑指 Offer 24. 反转链表
- 剑指 Offer 25. 合并两个排序的链表
- 剑指 Offer 26. 树的子结构
- 剑指 Offer 39. 数组中出现次数超过一半的数字
- 剑指 Offer 42. 连续子数组的最大和
题目收藏
不含重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
滑动窗口:左边界l, 右边界i, 右边界从0~len-1,用unordered_map记录字符上一次出现的位置,如果出现过就把左边界移动到max(l,字符上次出现的位置+1)
每次左边界移动,都是从含有一个重复的字符到不包含重复字符
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> last_exist;
int len=s.size();
int l=0;
int ans=0;
for(int i=0;i<len;i++){
if(last_exist.find(s[i])==last_exist.end()){
last_exist[s[i]]=i;
ans=max(ans,i-l+1);
}
else{
l=max(l,last_exist[s[i]]+1);
last_exist[s[i]]=i;
ans=max(ans,i-l+1);
}
}
return ans;
}
};

最长公共子串
给定两个字符串,求这两个字符串的不包含数字的最长公共子串的长度。
#include<bits/stdc++.h>
using namespace std;
const int N = 10010;
char s1[N],s2[N];
int res, f[N];
int main()
{
scanf("%s %s", s1 , s2);
int l = strlen(s1), r = strlen(s2);
for (int i = 1; i <= l; i++ )//将s1的长度看作物品数量(对应01背包)
{
for (int j = r; j>=1; j--)//s2的长度看作背包容量(对应01背包)
{
if (s1[i-1] == s2[j-1] && s1[i-1] > '9' && s2[j-1] > '9')//将s2的每个字符看作物品(体积为1,价值为x,其中x只有满足条件(满足相等)才有价值1,否则为0,<既然都为0了,为啥还要放进背包呢?>)
{
f[j] = f[j - 1] + 1;//背包的价值
res = max(res, f[j]);//res记录每次的最大值
}
else f[j] = 0;//都不满足,即所有物品价值为0,所以背包总价值也为0
}
}
printf("%d\n", res);
return 0;
}
剑指 Offer
剑指 Offer 05. 替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
- c++字符串可以修改,因为
i一定小于j,所以可能原地修改 - 从后往前,先得出修改后的长度,时间复杂度
O
(
n
)
O(n)
O(n)
class Solution { public: string replaceSpace(string s) { int n=s.size(); int num=0; for(int i=0;i<n;i++) if(s[i]==' ') num++; s.resize(n + 2 * num); for(int i=n-1,j=n-1+num*2;i<j;){ //i,j>=0也可 if(s[i]==' '){ s[j]='0';s[j-1]='2';s[j-2]='%';j-=3;i--; } while(i>=0 && j>=0 && s[i]!=' ') {//这一直报错,因为当i--后可能变为负的 s[j]=s[i];i--;j--; } } return s; } };
剑指 Offer 03. 数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
-
哈希表空间 O ( n ) O(n) O(n)
-
原地交换时间和哈希一样是 O ( n ) O(n) O(n),空间 O ( 1 ) O(1) O(1)

class Solution { public: int findRepeatNumber(vector<int>& nums) { int i=0; while(i<nums.size()){ if(nums[i]!=i) { if(nums[nums[i]]!=nums[i])//因为都在[0,n)之间,不会越界 swap(nums[i],nums[nums[i]]); else return nums[i]; } else i++; } return -1; } };
剑指 Offer 04. 二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
基准是右上角或者左下角,这样才可以剔除一行或一列;左上角无法剔除,无法缩小查找范围
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int n=matrix.size();
if(n==0) return false;
int m=matrix[0].size();
int r=0,c=m-1;
while(r<n && c>=0){
if(matrix[r][c]==target) return true;
else if(target<matrix[r][c]) c--;
else r++;
}
return false;
}
};
剑指 Offer 09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
class CQueue {
//两个栈,一个出栈,一个入栈
private Stack<Integer> stack1;
private Stack<Integer> stack2;
public CQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
if(!stack2.isEmpty()){
return stack2.pop();
}else{
while(!stack1.isEmpty()){
stack2.push(stack1.pop());
}
return stack2.isEmpty() ? -1 : stack2.pop();
}
}
}
剑指 Offer 07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
递推参数: 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder = preorder;
for(int i = 0; i < inorder.size(); i++)
dic[inorder[i]] = i;
return recur(0, 0, inorder.size() - 1);
}
private:
vector<int> preorder;
unordered_map<int, int> dic;
TreeNode* recur(int root, int left, int right) {
if(left > right) return nullptr; // 递归终止
TreeNode* node = new TreeNode(preorder[root]); // 建立根节点
int i = dic[preorder[root]]; // 划分根节点、左子树、右子树
node->left = recur(root + 1, left, i - 1); // 开启左子树递归
node->right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
return node; // 回溯返回根节点
}
};
剑指 Offer 06. 从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
从头遍历链表,入栈,再出栈。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
stack<ListNode*> sk;
vector<int> s;
ListNode* pNode=head;
while(pNode!=nullptr){
sk.push(pNode);
pNode=pNode->next;
}
while(!sk.empty()){
pNode=sk.top();
s.push_back(pNode->val);
sk.pop();
}
return s;
}
};
剑指 Offer 11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
输入:numbers = [3,4,5,1,2]
输出:1
输入:numbers = [2,2,2,0,1]
输出:0
class Solution {
public:
int minArray(vector<int>& numbers) {
//二分
int n=numbers.size();
int l=0,r=n-1;
int mid=l;//初始化为l,当numbers直接递增时
int ans=numbers[0];
while(numbers[l]>=numbers[r]){
if(l+1==r) {
mid=r;break;
}
mid=(l+r)>>1;
if(numbers[mid]==numbers[l] && numbers[mid]==numbers[r]){
for(int i=0;i<n;i++)
ans=min(ans,numbers[i]);
return ans;
}
if(numbers[mid]>=numbers[l]) l=mid;
else if(numbers[mid]<=numbers[r]) r=mid;
}
return numbers[mid];
}
};
- 按照旋转规则,第一个元素应该大于等于最后一个元素,特例
[1,2,3],此时,不进while()直接return numbers[mid]=numbers[0] - 若中间元素位于前面的递增子数组,那么它应该大于等于第一个指针指向的元素—>将第一个指针移到mid

剑指 Offer 12. 矩阵中的路径
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
rows = board.size();
cols = board[0].size();
for(int i = 0; i < rows; i++) {
for(int j = 0; j < cols; j++) {
if(dfs(board, word, i, j, 0)) return true;
}
}
return false;
}
private:
int rows, cols;
bool dfs(vector<vector<char>>& board, string word, int i, int j, int k) {
if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k]) return false;
if(k == word.size() - 1) return true;
board[i][j] = '\0';//已经用过这个字符了
bool res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = word[k];//回溯到上一层,恢复现场
return res;
}
};
剑指 Offer 27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
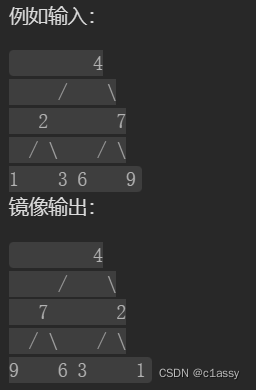
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(root == nullptr) return nullptr;
stack<TreeNode*> stack;
stack.push(root);
while (!stack.empty())
{
TreeNode* node = stack.top();
stack.pop();
if (node->left != nullptr) stack.push(node->left);
if (node->right != nullptr) stack.push(node->right);
TreeNode* tmp = node->left;
node->left = node->right;
node->right = tmp;
}
return root;
}
};
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if (root == nullptr) return nullptr;
TreeNode* tmp = root->left;
root->left = mirrorTree(root->right);
root->right = mirrorTree(tmp);
return root;
}
};
剑指 Offer 28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
bool isSymmetric(Treenode* root){
if(root==NULL) return false;
return check(root->left,root->right);
}
bool check(Treenode* u, Treenode* v){
if(u==NULL && v==NULL) return true;
if(u==NULL || v==NULL || u->val!=v->val) return false;
return check(u.left, v.right) && check(u.right, v.left);
}
class Solution {
public:
bool check(TreeNode *u, TreeNode *v) {
queue <TreeNode*> q;
q.push(u); q.push(v);
while (!q.empty()) {
u = q.front(); q.pop();
v = q.front(); q.pop();
if (!u && !v) continue;
if ((!u || !v) || (u->val != v->val)) return false;
q.push(u->left);
q.push(v->right);
q.push(u->right);
q.push(v->left);
}
return true;
}
bool isSymmetric(TreeNode* root) {
return check(root, root);
}
};
剑指 Offer 29. 顺时针打印矩阵
观察发现可以一圈一圈地输出,每圈的左上角可以表示成(start,start),循环继续的条件是n>start*2 && m>start*2,每圈可以分为从左到右,从上到下。。四步,每步打印的范围是start~m-1-start。。但是有的圈并不总是由这四步组成
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
int n=matrix.size();
if(n==0) return {};
int m=matrix[0].size();
int start=0;
while(n>start*2 && m>start*2){
int endX=m-1-start;
int endY=n-1-start;
for(int i=start;i<=endX;i++) res.push_back(matrix[start][i]);
for(int i=start+1;i<=endY;i++) res.push_back(matrix[i][endX]);
if(start<endY) for(int i=endX-1;i>=start;i--) res.push_back(matrix[endY][i]);
if(start<endX) for(int i=endY-1;i>start;i--) res.push_back(matrix[i][start]);
start++;
}
return res;
}
};
剑指 Offer 30. 包含min函数的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
借助一个辅助栈,其包含的是一个非递增序列–>如果新入栈的元素大于之前的最小值,仍然往辅助栈中压入该最小值,否则压入新入栈的元素
class MinStack {
stack<int> x_stack;
stack<int> min_stack;
public:
MinStack() {
min_stack.push(INT_MAX);
}
void push(int x) {
x_stack.push(x);
min_stack.push(::min(min_stack.top(), x));
}
void pop() {
x_stack.pop();
min_stack.pop();
}
int top() {
return x_stack.top();
}
int min() {
return min_stack.top();
}
};
剑指 Offer 31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
借助一个栈来模拟,先按照压入顺序入栈,如果弹出序列的j在栈顶,就弹出;否则,继续压入…
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> s;
int n=pushed.size();
for(int i=0,j=0;i<n;i++){
s.push(pushed[i]);
while(j<n &&!s.empty()&& popped[j]==s.top()) {
s.pop();j++;
}
}
if(s.empty()) return true;
else return false;
}
};
剑指 Offer 32 - I. 从上到下打印二叉树
二叉树的层序遍历/BFS
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
if(root==NULL) return {};
vector<int> res;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
auto t=q.front();
res.push_back(t->val);
q.pop();
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
return res;
}
};
剑指 Offer 32 - II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行
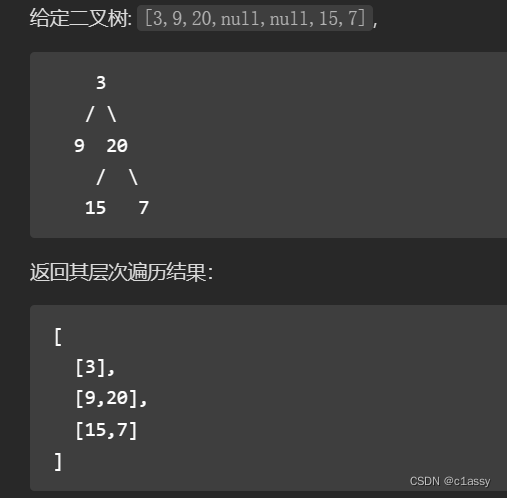
因为每次在队列中的都属于同一层。所以,循环q.size()次,对每个结点的处理不变。
vector<vector<int>> levelOrder(TreeNode* root) {
if(root==NULL) return {};
queue<TreeNode*> q;
q.push(root);
vector<vector<int>> ans;
while(!q.empty()){
vector<int> res;
int cnt=q.size();
for(int i=0;i<cnt;i++){
auto t=q.front();
q.pop();
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
res.push_back(t->val);
}
ans.push_back(res);
}
return ans;
}
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
输入: [1,6,3,2,5]
输出: false输入: [1,3,2,6,5]
输出: true
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
return verify(postorder,0,postorder.size()-1);
}
bool verify(vector<int>& postorder,int left,int right){
if(left>=right) return true;
int root=postorder[right];
int i=left;
while(i<=right && postorder[i]<root) i++;
int j=i;
while(j<=right && postorder[j]>root) j++;//必须是递增的,所哟从i之后的都要大于root
return j==right && verify(postorder,left,i-1)&&verify(postorder,i,right-1);
}
};
剑指 Offer 34. 二叉树中和为某一值的路径
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
void dfs(TreeNode* root, int target){
if(root==nullptr) return;
target-=root->val;
path.push_back(root->val);
if(root->left==nullptr && root->right==nullptr && target==0) ans.push_back(path);
dfs(root->left,target);
dfs(root->right,target);
//回溯时的恢复
path.pop_back();
}
vector<vector<int>> pathSum(TreeNode* root, int target) {
dfs(root,target);
return ans;
}
};
剑指 Offer 15. 二进制中1的个数
可能输入负数,如0x80000000。负数右移:10001010>>3=11110001
- 循环的次数等于整数二进制的位数
int NumberOf1(int n){ int count=0; unsigned int flag=1; while(flag){ if(n&flag) count++; flag=flag<<1; } return count; } - 二进制数字n中1的个数
n&(n-1)把n最右边的1变为0int NumberOf1(int n){ int count=0; while(n){ count++; n=n&(n-1); } return count; }
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

class Solution {
public:
vector<int> exchange(vector<int>& nums)
{
int i = 0, j = nums.size() - 1;
while (i < j)
{
while(i < j && (nums[i] & 1) == 1) i++;
while(i < j && (nums[j] & 1) == 0) j--;
swap(nums[i], nums[j]);
}
return nums;
}
};
(nums[i] & 1) == 1)这里是一个判断数字属于数组的前半部分还是后半部分的函数。
22.链表中倒数第k个节点
只遍历链表一次:
思路:第一个指针从头节点开始走k-1步,第二个指针保持不动;从第k步开始,第二个指针也开始从头结点动(由于两个指针相差k-1,所以当第一个指针到末尾时,第二个指针刚好指向倒数第k个节点)
扩展1:求链表的中间结点。一个指针一次走一步,另一个一次走两步;当走得快的指针走到末尾时,走得慢的指针刚好在链表中间。(扩展2:若走得快的追上了走得慢的,说明链表中存在环;没有追上说明一定不存在)
剑指 Offer II 022. 链表中环的入口节点
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
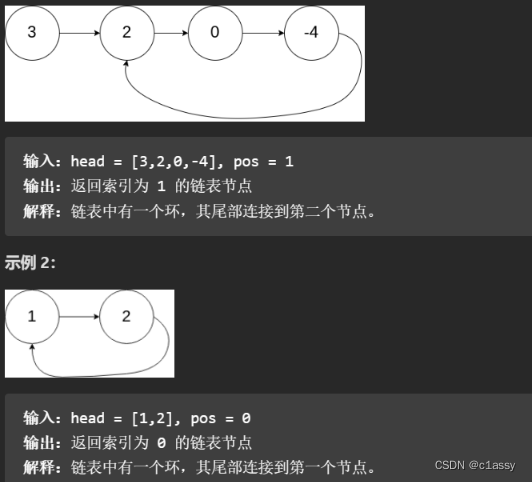
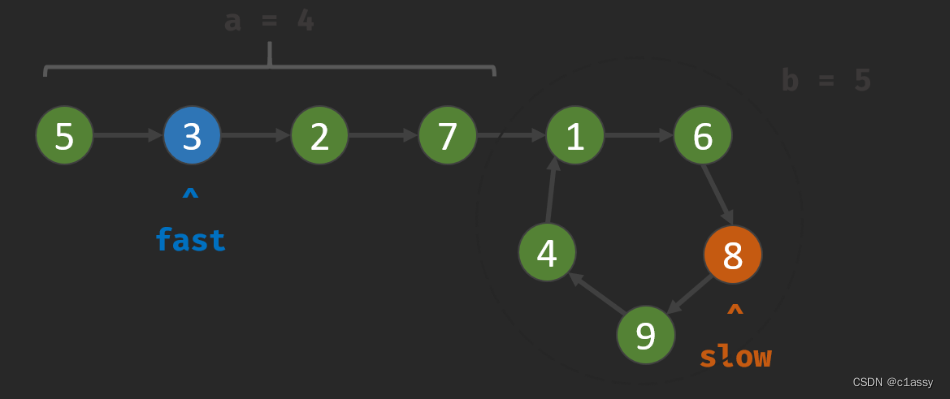
第一轮相遇:
fast 走的步数是 slow 步数的 2 倍,即 f = 2 s f=2s f=2s
fast 比 slow 多走了 n 个环的长度,即 f = s + n b f=s+nb f=s+nb
–> f = 2 n b , s = n b f=2nb, s=nb f=2nb,s=nb
目前,slow 指针走过的步数为 nb 步。因此,我们只要想办法让 slow 再走 a 步停下来,就可以到环的入口
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while (true) {
if (fast == nullptr || fast->next == nullptr) return nullptr;
fast = fast->next->next;
slow = slow->next;
if (fast == slow) break;
}
fast = head;//fast走了a步->slow也走了a步
while (slow != fast) {
slow = slow->next;
fast = fast->next;
}
return fast;//不能是head
}
};
剑指 Offer 24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* tmp=head;
ListNode* pPrev=nullptr;
ListNode* pReversedHead=nullptr;
while(tmp!=nullptr){
ListNode* pNext=tmp->next;//防止链表断裂,复制
if(pNext==nullptr) pReversedHead=tmp;//最后一个结点就是反转后的头结点
tmp->next=pPrev;
pPrev=tmp;
tmp=pNext;//注意这两句的顺序
}
return pReversedHead;
}
};
剑指 Offer 25. 合并两个排序的链表
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* dump=new ListNode(0);
ListNode* cur=dump;
while(l1!=nullptr && l2!=nullptr){
if(l1->val == l2->val || l1->val > l2->val) {
cur->next=l2;l2=l2->next;
}
else {
cur->next=l1;l1=l1->next;
}
cur=cur->next;
}
if(l1==nullptr) cur->next=l2;
else cur->next=l1;
return dump->next;
}
};
递归:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1==nullptr) return l2;
if(l2==nullptr) return l1;
ListNode* pMergeHead=nullptr;
if(l1->val < l2->val){
pMergeHead=l1;
pMergeHead->next=mergeTwoLists(l1->next,l2);
}
else{
pMergeHead=l2;
pMergeHead->next=mergeTwoLists(l1,l2->next);
}
return pMergeHead;
}
};
剑指 Offer 26. 树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
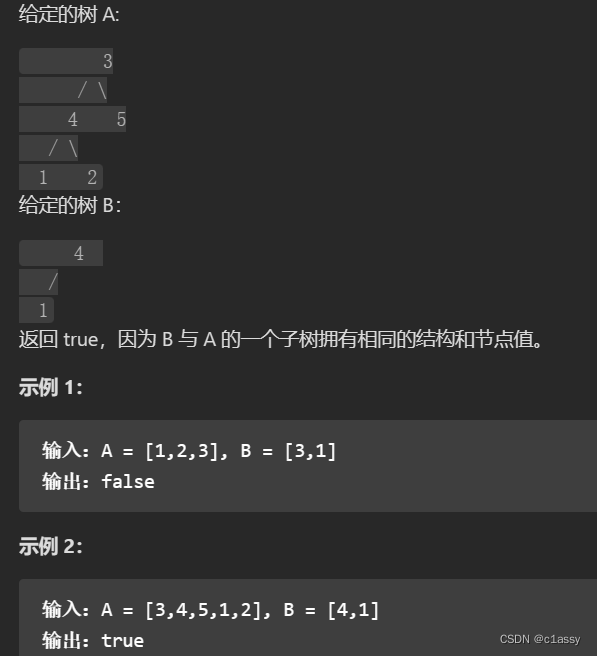
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
bool result=false;
if(A!=nullptr && B!=nullptr){//找到节点值相同的点,然后判断其左右子树是否相同
if(A->val==B->val) result=doesTree1HasTree2(A,B);
//没找到节点值相同的点,继续找(递归看其左右子树)
if(!result) result=isSubStructure(A->left,B);
if(!result) result=isSubStructure(A->right,B);
}
return result;
}
bool doesTree1HasTree2(TreeNode* A,TreeNode* B){
if(B==nullptr) return true;//注意这两句的顺序
if(A==nullptr) return false;
if(A->val!=B->val) return false;
return doesTree1HasTree2(A->left,B->left) && doesTree1HasTree2(A->right,B->right);
}
};
剑指 Offer 39. 数组中出现次数超过一半的数字
摩尔投票法: 核心理念为 票数正负抵消。此方法时间和空间复杂度分别为
O
(
N
)
O(N)
O(N) 和
O
(
1
)
O(1)
O(1)

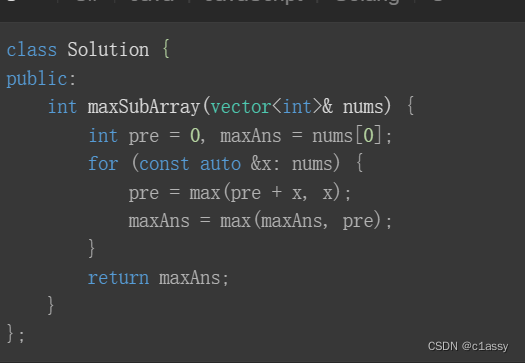
剑指 Offer 42. 连续子数组的最大和
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
int res=nums[0],before=nums[0],tmp;
for(int i=1;i<n;i++){
if(before<=0) tmp=nums[i];
else tmp=before+nums[i];
before=tmp;//优化成before=max(),res=max(before)
res=max(res,tmp);
}
return res;
}
};