策略网络和价值网络的架构
我们知道状态价值函数
V
π
(
s
)
=
∑
a
π
(
a
∣
s
)
⋅
Q
π
(
s
,
a
)
V_\pi(s)=\sum_a\pi(a|s)\cdot Q_\pi(s,a)
Vπ(s)=∑aπ(a∣s)⋅Qπ(s,a),在策略学习中,我们用神经网络去近似
π
\pi
π函数,得到策略网络
π
(
a
,
s
;
θ
)
\pi(a,s;\theta)
π(a,s;θ)。但我们发现要更新训练策略网络时,需要动作价值
q
t
q_t
qt,我们用另一个神经网络去近似动作价值函数
Q
π
Q_\pi
Qπ,得到价值网络
q
(
s
,
a
;
w
)
q(s,a;w)
q(s,a;w),其中
w
w
w表示神经网络中可训练的参数。有了以上两个神经网络,我们就可以近似出状态价值函数:
V
π
(
s
)
=
∑
a
π
(
a
∣
s
)
⋅
Q
π
(
s
,
a
)
≈
∑
a
π
(
a
∣
s
;
θ
)
⋅
q
(
s
,
a
;
w
)
V_\pi(s)=\sum_a\pi(a|s)\cdot Q_\pi(s,a) \approx \sum_a\pi(a|s;\theta) \cdot q(s,a;w)
Vπ(s)=∑aπ(a∣s)⋅Qπ(s,a)≈∑aπ(a∣s;θ)⋅q(s,a;w)
V
π
(
s
;
θ
,
w
)
=
∑
a
π
(
a
∣
s
;
θ
)
⋅
q
(
s
,
a
;
w
)
V_\pi(s;\theta,w)=\sum_a\pi(a|s;\theta) \cdot q(s,a;w)
Vπ(s;θ,w)=∑aπ(a∣s;θ)⋅q(s,a;w)
而其中的策略网络
π
(
a
∣
s
;
θ
)
\pi(a|s;\theta)
π(a∣s;θ)被称为 Actor(演员),价值网络
q
(
s
,
a
;
w
)
q(s,a;w)
q(s,a;w)被称为 Critic(评委)。
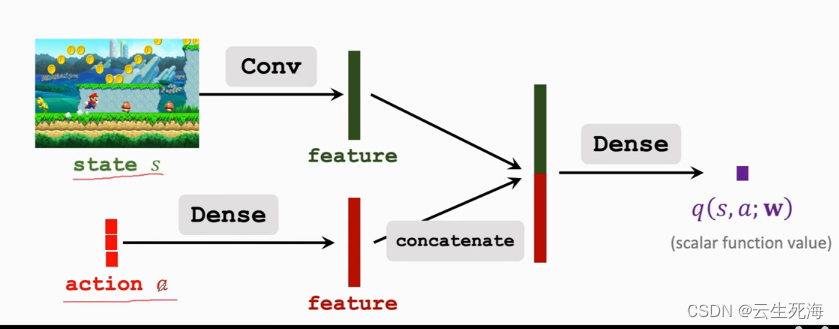
价值网络的输入是状态s,输出是每个动作的价值。动作空间A中有多少种动作,那么价值网络的输出就是多少维的向量,向量每个元素对应一个动作。
训练两个神经网络
训练策略网络(Actor)
训练策略网络的基本想法,根据当前状态s,自己的动作a和评委的打分
q
^
=
q
(
s
,
a
;
w
)
\widehat{q}=q(s,a;w)
q
=q(s,a;w)计算近似策略梯度,然后更新自己的参数
θ
\theta
θ
训练价值网络(Critic)
我们发现训练策略网络(演员)的方法只是让演员更迎合评委的喜好而已。 因此,评委的水平也很重要,只有当评委的打分
q
^
\widehat{q}
q
真正反映出动作价值
Q
π
Q_\pi
Qπ演员的水平才能真正提高。
可以用 SARSA 算法更新w,提高评委的水平。每次从环境中观测到一个奖励r,把 r看做是真相,用r来校准评委的打分。
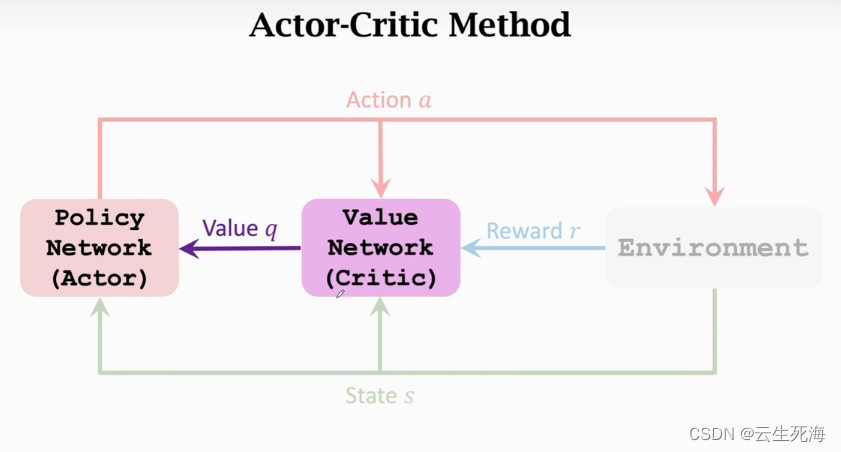
训练流程
- 观测到当前状态 s t s_t st,根据策略网络做决策: a t ∼ π ( . ∣ s t ; θ ) a_t \sim \pi(.|s_t;\theta) at∼π(.∣st;θ) ,并让智能体执行动作 a t a_t at 。
- 从环境中观测到奖励 r t r_t rt和新的状态 s t + 1 s_{t+1} st+1。
- 根据策略网络做决策: a t + 1 ∼ π ( . ∣ s t ; θ ) a_{t+1} \sim \pi(.|s_t;\theta) at+1∼π(.∣st;θ),但不让智能体执行动作 a t + 1 a_{t+1} at+1
- 让价值网络打分: q t ^ = q ( s t , a t , w ) \widehat{q_t} = q(s_t,a_t,w) qt =q(st,at,w)和 q t + 1 ^ = q ( s t + 1 , a t + 1 , w ) \widehat{q_{t+1}} = q(s_{t+1},a_{t+1},w) qt+1 =q(st+1,at+1,w)
- 计算 TD 目标和 TD 误差: y t ^ = r t + γ ⋅ q t + 1 ^ \widehat{y_t} = r_t+\gamma \cdot \widehat{q_{t+1}} yt =rt+γ⋅qt+1 和 L t ( w ) = 1 2 [ q t ^ − y t ^ ] 2 L_t(w) =\frac{1}{2} [\widehat{q_t} - \widehat{y_t}]^2 Lt(w)=21[qt −yt ]2
- 更新价值网络 q q q: w = w − α ⋅ L t ⋅ ∂ L t ( w ) ∂ w ∣ w = w t w = w - \alpha \cdot L_t \cdot \frac{\partial L_t(w)}{\partial w}|_{w=w_t} w=w−α⋅Lt⋅∂w∂Lt(w)∣w=wt
- 更新策略网络 π \pi π: θ = θ + β ⋅ q t ^ ⋅ ∂ l o g π ( a ∣ s ; θ ) ∂ θ \theta = \theta + \beta \cdot \widehat{q_t} \cdot \frac{\partial log\pi(a|s;\theta)}{\partial \theta} θ=θ+β⋅qt ⋅∂θ∂logπ(a∣s;θ)