基本概念
折扣回报(Discounted Return)
在 MDP 中,通常使用折扣回报 (discounted return),给未来的奖励做折扣。折扣回报的定义如下:
U
t
=
R
t
+
γ
R
t
+
1
+
γ
2
R
t
+
2
+
γ
3
R
t
+
3
+
.
.
.
U_t = R_t+\gamma R_{t+1}+\gamma ^2R_{t+2}+\gamma ^3R_{t+3}+...
Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+...
这里的
γ
∈
[
0
,
1
]
\gamma \in [0,1]
γ∈[0,1]叫折扣率。对待越久远的未来,给奖励打的折扣越大。
U
t
U_t
Ut是一个随机变量,随机性来自于t时刻之后的所有状态和动作
动作价值函数(Action-value function)
假设我们已经观测到状态
s
t
s_t
st,而且做完决策,选中动作
a
t
a_t
at。那么
U
t
U_t
Ut中的随机性来自于
t
+
1
t+1
t+1时刻起的所有的状态和动作:
S
t
+
1
,
A
t
+
1
,
S
t
+
2
,
A
t
+
2
,
.
.
.
,
S
n
,
A
n
S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_{n},A_{n}
St+1,At+1,St+2,At+2,...,Sn,An
Q
π
(
s
t
,
a
t
)
=
E
S
t
+
1
,
A
t
+
1
,
S
t
+
2
,
A
t
+
2
,
.
.
.
,
S
n
,
A
n
[
U
t
∣
S
t
=
s
t
,
A
t
=
a
t
]
Q_\pi(s_t,a_t)=E_{{S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_{n},A_{n}}}[U_t | St=s_t,A_t=a_t]
Qπ(st,at)=ESt+1,At+1,St+2,At+2,...,Sn,An[Ut∣St=st,At=at]
期望中的
S
t
=
s
t
S_t=s_t
St=st和
A
t
=
a
t
A_t=a_t
At=at是条件,意思是已经观测到
S
t
S_t
St与
A
t
A_t
At的值。条件期望的结果
Q
π
(
s
t
,
a
t
)
Q_\pi(s_t,a_t)
Qπ(st,at)被称作动作价值函数 (action-value function)。
作用:根据策略 π , Q π ( s , a ) \pi,Q_\pi(s,a) π,Qπ(s,a)来估计当前状态 s s s对于智能体选择动作 a a a是否明智,得到好的效果
最优动作价值函数(Optimal action-value function)
最优动作价值函数
Q
∗
(
s
t
,
a
t
)
Q^*(s_t,a_t)
Q∗(st,at)用最大化消除策略
π
\pi
π:
Q
∗
(
s
t
,
a
t
)
=
m
a
x
π
Q
π
(
s
t
,
a
t
)
Q^*(s_t,a_t)= \mathop{max}\limits_{\pi} Q_\pi(s_t,a_t)
Q∗(st,at)=πmaxQπ(st,at)
Q
∗
Q^*
Q∗可以对当前状态
s
s
s对执行动作
a
a
a做评测,得到好坏程度
可以这样理解
Q
∗
Q^*
Q∗: 已知
s
t
s_t
st和
a
t
a_t
at,不论未来采取什么样的策略
π
\pi
π,回报
U
t
U_t
Ut的期望不可能超过
Q
∗
Q*
Q∗。
最优动作价值函数的用途:假如我们知道 Q ∗ Q^* Q∗ ,我们就能用它做控制。
Deep Q-Network(DQN)
我们希望知道最优动作价值函数 Q ∗ Q^* Q∗ ,因为 Q ∗ Q^* Q∗ 就像先知一样,可以在 t t t时刻就预见 t t t到 n n n时刻之间的累计奖励的期望。假如我们知道 Q ∗ Q^* Q∗ ,我们就可以根据 Q ∗ Q^* Q∗ 的值选择最优动作(best action) a ∗ = a r g m a x x a Q ∗ ( s , a ) a^*=\mathop{argmax}x_aQ^*(s,a) a∗=argmaxxaQ∗(s,a),然后就可以最大化未来的累计奖励。
我们不知道
Q
∗
Q^*
Q∗ 的函数,我们希望用神经网络
Q
(
s
,
a
;
w
)
Q(s,a;w)
Q(s,a;w)去近似学习
Q
∗
Q^*
Q∗
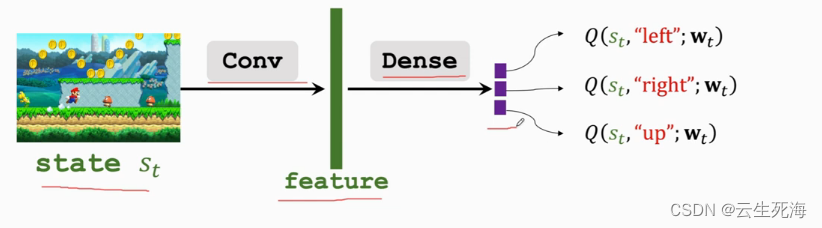
我们观测到
t
t
t 时刻的状态
s
t
s_t
st,然后根据 DQN 选出能够使
t
t
t时刻 Q 值最大的动作
a
t
a_t
at,执行动作
a
t
a_t
at,得到奖励
r
t
r_t
rt,再根据环境状态转移的概率函数得到下一个状态
s
t
+
1
s_{t+1}
st+1,依次进行,直到这一回合结束。如下图所示:
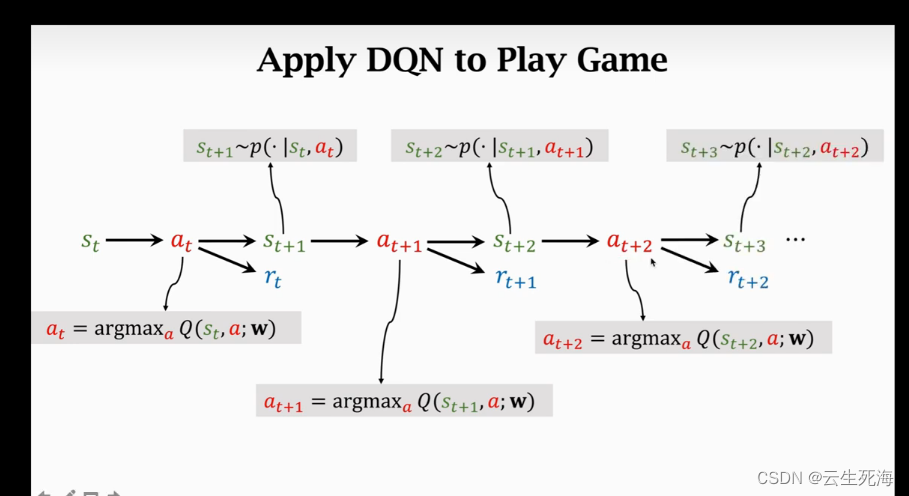
时间差分算法(Temporal Difference Learning)
我们有一个模型
Q
(
s
,
d
;
w
)
Q(s,d;w)
Q(s,d;w),其中 s是起点,d 是终点,w 是参数。
假如s和d直接有一地点c
模型估计
Q
(
s
,
d
,
w
)
=
1000
m
i
n
Q(s,d,w) = 1000min
Q(s,d,w)=1000min
实际s到c花费300min
Q
(
c
,
d
,
w
)
=
600
m
i
n
Q(c,d,w) = 600min
Q(c,d,w)=600min
更新估计 300+600 = 900min
我们把y = 900min称为TD target 这样的估计更准确,也不用跑完全程。
用 TD 算法训练 DQN(TD Learning for DQN)
折扣回报
U
t
=
R
t
+
γ
R
t
+
1
+
γ
2
R
t
+
2
+
γ
3
R
t
+
3
+
.
.
.
U_t = R_t+\gamma R_{t+1}+\gamma ^2R_{t+2}+\gamma ^3R_{t+3}+...
Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+...
U
t
=
R
t
+
γ
⋅
U
t
+
1
U_t = R_t+\gamma \cdot U_{t+1}
Ut=Rt+γ⋅Ut+1
DQN 在
t
t
t时刻的输出:
Q
(
s
t
,
a
t
;
w
)
Q(s_t,a_t;w)
Q(st,at;w) ,是对
U
t
U_t
Ut的估计;在
t
+
1
t+1
t+1时刻的输出
Q
(
s
t
+
1
,
a
t
+
1
;
w
)
Q(s_{t+1},a_{t+1};w)
Q(st+1,at+1;w),是对U_{t+1}的估计。因此,我们可以得到如下等式:
Q
(
s
t
,
a
t
;
w
)
≈
r
t
+
γ
⋅
Q
(
s
t
+
1
,
a
t
+
1
;
w
)
Q(s_t,a_t;w) \approx r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w)
Q(st,at;w)≈rt+γ⋅Q(st+1,at+1;w)
使用 TD learning 训练 DQN 流程:
1、在
t
t
t时刻做预测 Prediction:
Q
(
s
t
,
a
t
;
w
t
)
Q(s_t,a_t;w_t)
Q(st,at;wt)
2、计算 TD target:
y
t
=
r
t
+
γ
⋅
m
a
x
a
Q
(
s
t
+
1
,
a
;
w
t
)
y_t=r_t+\gamma \cdot \mathop{max}\limits_{a} Q(s_{t+1},a;w_t)
yt=rt+γ⋅amaxQ(st+1,a;wt)
3、计算损失函数 Loss(TD error):
L
t
=
1
2
[
Q
(
s
t
,
a
t
;
w
t
)
−
y
t
]
2
L_t=\frac{1}{2}[Q(s_t,a_t;w_t)-y_t]^2
Lt=21[Q(st,at;wt)−yt]2
4、做梯度下降更新参数
w
w
w:#
w
t
+
1
=
w
t
−
α
⋅
∂
L
t
∂
w
∣
w
=
w
t
w_{t+1}=w_t-\alpha \cdot \frac{\mathrm{\partial}L_t}{\mathrm{\partial}w}|_{w=w_t}
wt+1=wt−α⋅∂w∂Lt∣w=wt
.



![[工具]Pytorch-lightning的使用](https://img-blog.csdnimg.cn/d3001cffcd0b4da795f7d57e3b219fd1.png)
![shiro反序列化[cve_2016_4437]](https://img-blog.csdnimg.cn/b30d9e2b3d8a4a98b8a513349e20a234.png)