文章目录
- 有序数组和链表的对比
- 有序数组
- 有序链表
- 跳表
- 跳表的搜索
- 跳表的插入
- 跳表的删除
- 跳表完整Java实现代码(包含上面介绍的所有功能模块)
有序数组和链表的对比
有序数组
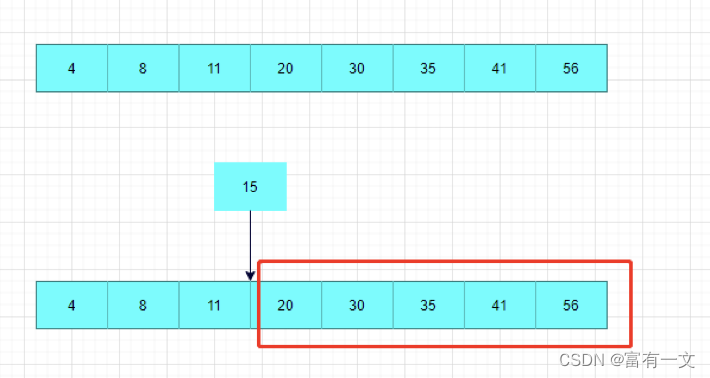
有序数组支持高效随机访问,可以使用二分查找使得查找的时间复杂度为O(lgn),但插入和删除的时间复杂度为O(n)。
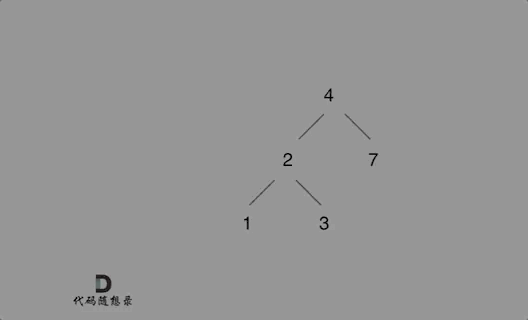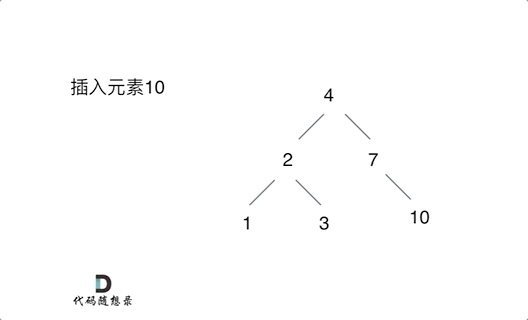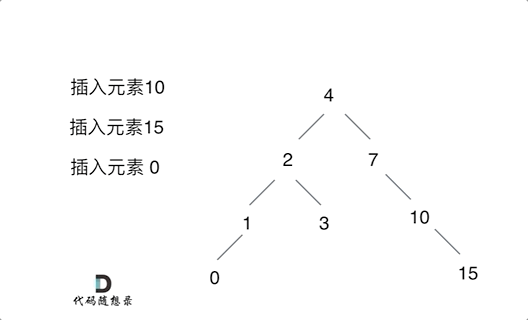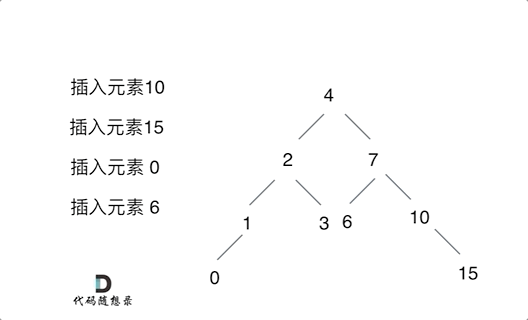
如图:先通过二分查找锁定插入位置,再移动该位置后面元素腾出空间,最后插入值
有序链表
有序链表在找到位置后,插入和删除快,但链表没有数组那样的高效随机访问,无法使用二分查找,只能一个节点一个节点遍历,所以链表查找、插入、删除的时间复杂度均为O(n)。
如图:先顺序遍历找到指定位置,插入即可

可以看出,有序数组和有序链表各有优势,有序数组查找快但插入慢,有序链表插入块但查找慢,有没有什么办法让有序链表搜索、添加、删除的平均时间复杂度降低至O(logn)?
跳表
有,一条有序链表不够,可以多加几条。(空间换时间)
如图:
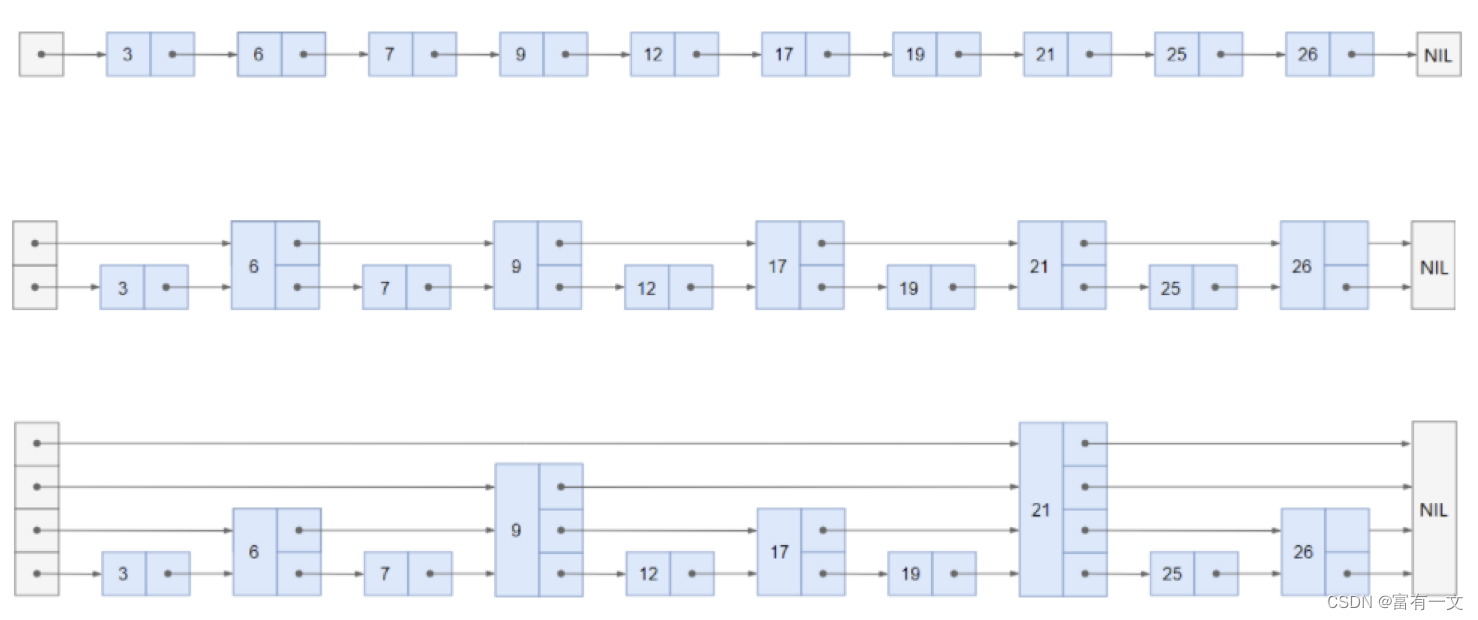
跳表的搜索
1、从顶层链表的首元素开始,从左往右搜索,直至找到一个大于或等于目标的元素,或者到达当前层链表的尾部
2、如果该元素等于目标元素,则表明该元素已被找到
3、如果该元素大于目标元素或已到达链表的尾部,则退回到当前层的前一个元素,然后转入下一层进行搜索
如图:

寻找值为19的结点,先在最上面层查找到第一个大于19的结点21,记录它前面的结点17,再从下一层的17结点开始寻找,能快速找到19结点。
跳表的插入
1、在插入节点之前,我们需要搜索得到插入的位置
2、插入元素时,需要随机决定新添加元素的层数
如图所示:

插入17需要找到所有有序链表的17节点前一个结点。
跳表的删除
如果要删除节点,则把节点和对应的所有索引节点全部删除即可。当然,要删除节点时需要先搜索得到该节点,搜索过程中可以把路径记录下来,这样删除索引层节点的时候就不需要多次搜索了。
删除一个元素后,整个跳表的层数可能会降低。
如图所示:

跳表完整Java实现代码(包含上面介绍的所有功能模块)
/**
* @Author hepingfu
* @Date 2023/05/09/16:03
* @Version 1.0
*/
public class SkipList {
/**
* 最高层数16层
*/
private static final int MAX_LEVEL = 16;
/**
* 每层上升概率0.5,新节点的高度是随机的,这里给定概率0.5
*/
private static final double P = 0.5;
/**
* 当前有效层数
*/
private int level;
/**
* 伪首节点,不存放任何键值对
*/
private Node first;
/**
* 默认构造器创建伪首节点
*/
public SkipList() {
first = new Node(null, null, MAX_LEVEL);
}
/**
* 节点类
*/
private static class Node {
Integer key;
Integer value;
Node[] nexts;
public Node(Integer key, Integer value, int level) {
this.key = key;
this.value = value;
nexts = new Node[level];
}
@Override
public String toString() {
return key + ":" + value + "_" + nexts.length;
}
}
/**
* 查找
* @param key
* @return
*/
public Integer get(Integer key) {
keyCheck(key);
Node node = first;
for (int i = level - 1; i >= 0; i--) {
/**
* 当下一个节点非空,
* 且当前键小于下一个节点的键时,
* while循环继续
*/
while (node.nexts[i] != null
&& key < node.nexts[i].key) {
node = node.nexts[i];
}
//相等直接返回,否则i减1,走下面一层
if (key == node.nexts[i].key) return node.nexts[i].value;
}
// for循环结束出来,就是没找到,返回空
return null;
}
/**
* 插入节点
* @param key
* @param value
* @return
*/
public Integer put(Integer key, Integer value) {
keyCheck(key);
Node node = first;
Node[] prevs = new Node[level]; // 记录每层前面的结点
for (int i = level - 1; i >= 0; i--) {
/**
* 当下一个节点非空,
* 且当前键小于下一个节点的键时,
* while循环继续
*/
while (node.nexts[i] != null
&& key < node.nexts[i].key) {
node = node.nexts[i];
}
if (key == node.nexts[i].key) { // 节点是存在的
Integer oldValue = node.nexts[i].value;
node.nexts[i].value = value;
return oldValue;
}
//prevs用来记录每一层要插入前的节点
prevs[i] = node;
}
// 新节点的层数,随机产生
int newLevel = randomLevel();
// 添加新节点
Node newNode = new Node(key, value, newLevel);
// 设置前驱和后继
for (int i = 0; i < newLevel; i++) {
if (i >= level) {
first.nexts[i] = newNode;
} else {
newNode.nexts[i] = prevs[i].nexts[i];
prevs[i].nexts[i] = newNode;
}
}
// 计算跳表的最终层数
level = Math.max(level, newLevel);
return null;
}
public Node remove(Integer key) {
keyCheck(key);
Node node = first;
Node[] prevs = new Node[level];
boolean exist = false;
for (int i = level - 1; i >= 0; i--) {
/**
* 当下一个节点非空,
* 且当前键小于下一个节点的键时,
* while循环继续
*/
while (node.nexts[i] != null
&& key < node.nexts[i].key) {
node = node.nexts[i];
}
prevs[i] = node;
if (key == node.nexts[i].key) exist = true;
}
if (!exist) return null;
// 需要被删除的节点
Node removedNode = node.nexts[0];
// 设置后继
for (int i = 0; i < removedNode.nexts.length; i++) {
prevs[i].nexts[i] = removedNode.nexts[i];
}
// 删除后更新跳表的层数
int newLevel = level;
while (--newLevel >= 0 && first.nexts[newLevel] == null) {
level = newLevel;
}
return removedNode;
}
/**
* 插入时level变化
* @return
*/
private int randomLevel() {
int level = 1;
while (Math.random() < P && level < MAX_LEVEL) {
level++;
}
return level;
}
/**
* 判断key是否违规
* @param key
*/
private void keyCheck(Integer key) {
if (key == null) {
throw new IllegalArgumentException("key must not be null.");
}
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("一共" + level + "层").append("\n");
for (int i = level - 1; i >= 0; i--) {
Node node = first;
while (node.nexts[i] != null) {
sb.append(node.nexts[i]);
sb.append(" ");
node = node.nexts[i];
}
sb.append("\n");
}
return sb.toString();
}
public static void main(String[] args) {
SkipList skipList = new SkipList();
for (int i = 0; i < 20; i++) {
skipList.put(i, i + 10);
}
System.out.println(skipList.toString());
}
}
ps:计划每日更新一篇博客,今日2023-05-07,日更第二十一天。(9号补更)
昨日更新:
leetcode 104——二叉树的最大深度