算法设计 || 第3题：多边形算法+分治算法解决循环赛问题（奇偶赛）

news2024/9/23 1:36:18

2022北京冬奥会在新冠疫情肆虐的情况下仍然成功举办，体现了我们国家和组织者的集体智慧。假设有项体育比赛有N=14个队伍需要和其他N-1=13只队伍进行循环赛,

如果偶数个队伍，每个队伍每天捉对赛一场，共进行N-1=13天比赛;

奇数个队伍会出现每天有一个队轮空，连续进行N=14天比赛;请编程输出每天的比赛安排。

（1）每个选手必须与其他n-1个选手各赛一次；

（2）每个选手一天只能赛一次；

（3）当n 是偶数，循环赛进行n-1天，当n是奇数，循环赛进行n天

方法1：多边形算法

package xunhuansai; // 声明包名
//Molly
 
import java.util.Scanner; // 导入Scanner类
 
public class RoundMatches { // 声明一个名为RoundMatches的公共类
 
    public static void main(String[] args) { // 声明主方法
        Scanner sc = new Scanner(System.in); // 创建Scanner对象
        int n = sc.nextInt(); // 从控制台读取一个整数
        makeTable(n); // 调用makeTable方法
    }
 
    private static void makeTable(int num) { // 声明一个名为makeTable的私有静态方法，入参为整型num
        int days = num - (num + 1) % 2; // 计算比赛天数
        for (int i = 0; i < days; i++) { // 循环比赛天数次
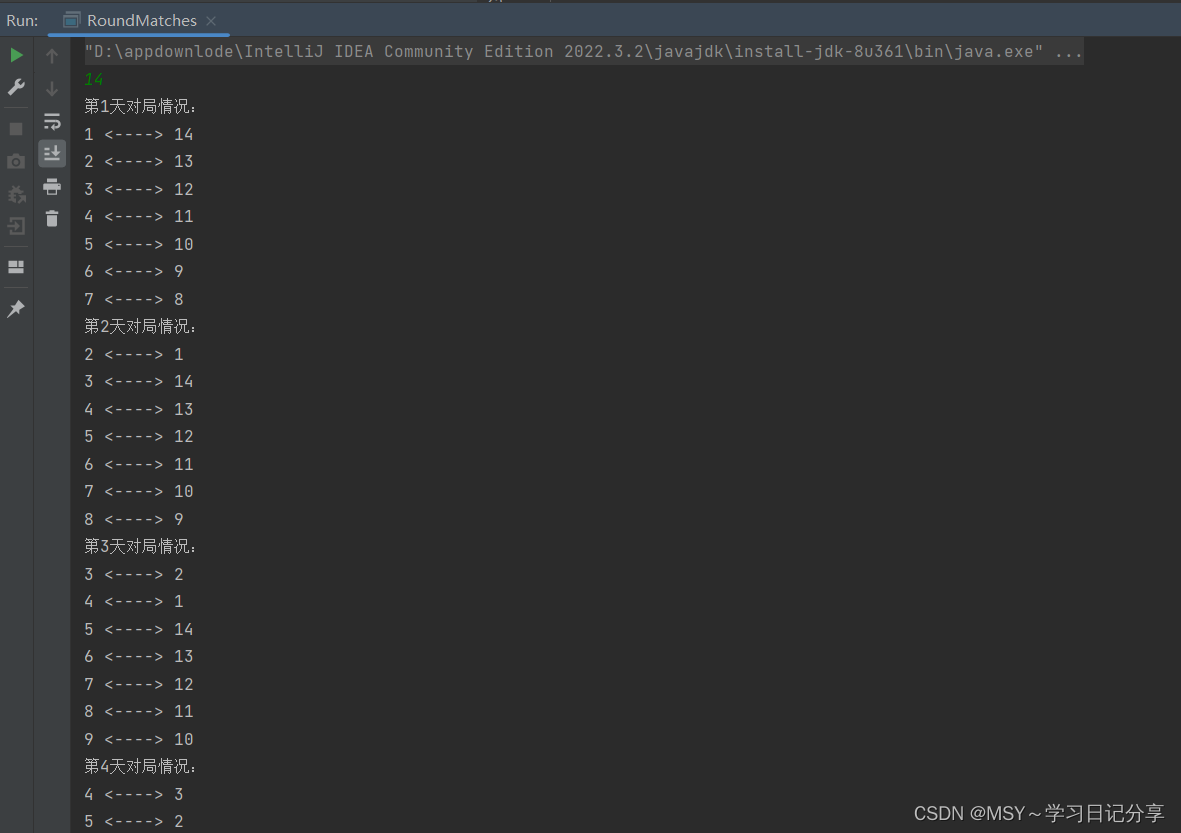
            System.out.println("第" + (i + 1) + "天对局情况："); // 输出比赛天数
            int len = num - 1; // 初始化len变量
            for (int j = 0; j < num / 2; j++) { // 循环比赛场次
                System.out.println(((i + j) % num + 1) + " <----> "
                        + ((i + j + len) % num + 1)); // 输出比赛对局情况
                len -= 2; // 更新len变量的值
            }
        }
    }
}

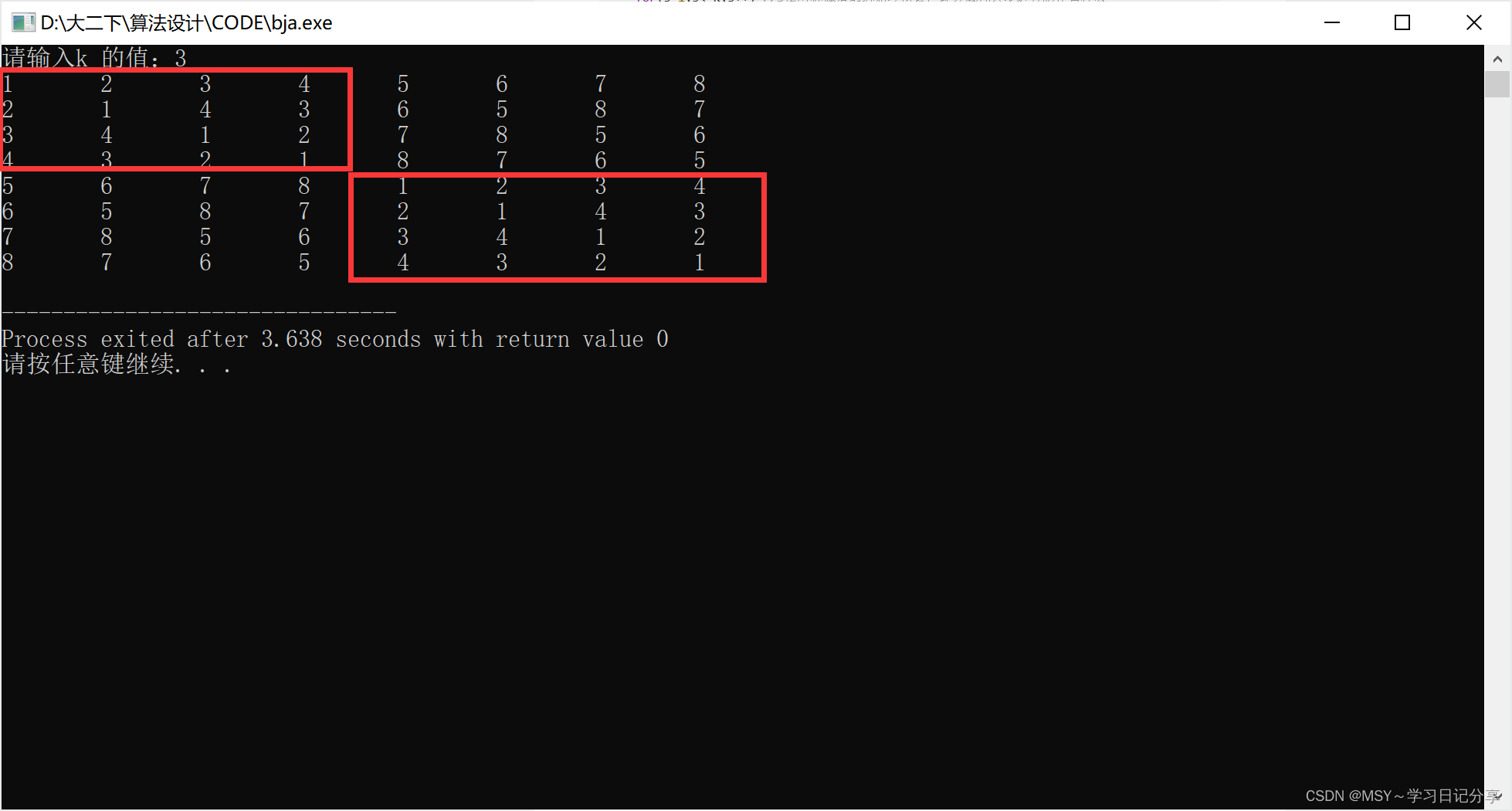
方法2：分治算法

限制条件：队伍数量必须是2K，否则无法划分！

//Molly 
#include<stdio.h>
#include<math.h>
#define N 50
int a[N][N];  //定义二维数组a用于存储生成的日程表
void Table(int k); //生成日程表的函数
void print(int k); //输出二维数组 
main()
{
    int k;
    printf("请输入k 的值：");
    scanf("%d",&k); //输入参与制作日程表的人数k
    Table(k); //调用Table函数生成日程表
    print(k); //调用print函数输出日程表
}
void Table(int k)//数组下标从1开始
{
    int i,j,s,t;
    int n=1;
    for(i=1;i<=k;i++)
        n*=2; //求出总人数n，即2的k次方
    
    for(i=1;i<=n;i++)
        a[1][i]=i; //初始化第一行排，按照顺序排好
    
    int m=1; //用来控制每一次填表时i行j列的起始填充位置
    for(s=1;s<=k;s++) //s指对称赋值的总循环次数，即分成几大步进行制作日程表
    {
        n=n/2; //每一步对称赋值后，总人数减半
        for(t=1;t<=n;t++) //t指明内部对称赋值的循环次数
            for(i=m+1;i<=2*m;i++)
                for(j=m+1;j<=2*m;j++)
                {
                    a[i][j+(t-1)*m*2]=a[i-m][j+(t-1)*m*2-m]; //右上角等于左上角的值
                    a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2]; //左下角等于右上角的值
                }
        m*=2; //每一步对称赋值后，填充起点位置乘以2
    }   
}
void print(int k)
{
    int i,j;
    int num=pow(2,k); //计算出日程表的大小，即总人数的平方
    for(i=1;i<=num;i++)                          
    {
        for(j=1;j<=num;j++)
        {
            printf("%d\t",a[i][j]); //输出二维数组a中的值，即生成的日程表
        }
         printf("\n"); //每一行输出完毕后换行
    }
}