1.算法描述

载波同步是相干解调的基础，不管对于模拟通信还是数字通信来说，只要是相干解调，接收端都必须提供同频同相的载波。当然，若采用基带传输，此时便没有载波同步的问题，因为没有频带调制，即没有乘以载波进行频谱搬移的过程。

位同步，也叫符号同步、定时同步、码元同步，只有数字通信才需要，数字通信中不管是基带传输还是频带传输都需要。这是因为数字通信中，是用波形中的几个采样点去代替一个符号，在接收端只需要对这些采样点中的一个进行判决，便可以恢复出这个符号。

实际通信中，由于信道的传输时延，接收两端的时钟偏移，接收端无法找到符号的最佳时刻来对其进行采样判决，这便使得接收端恢复出的数据与发送端的数据有误差。接收端若想在最佳采样时刻恢复发送端的数据，便要使得接收时钟与发送时钟同步，因此接收端要采取措施来调整接收端的采样时钟，这个同步的过程便定义为位同步。

这里，我们分析了通信中的4进制相移键控QPSK调制解调算法,并使用具有多种信号处理IP核且开发灵活的现场可编程逻辑门阵列(Field-Programmable Gate Array:FPGA)对该算法进行了硬件实现。对BPSK调制解调算法中的关键技术数控振荡器(Numerically controlled oscillator: NCO)、成型滤波器、载波同步与定时同步的基本原理进行了详细的分析。随后,基于通信系统的设计要求,分别选择Costas环和Gardner环用于载波和码元同步,并利用Matlab软件对同步环路的参数及功能进行了仿真验证。在Matlab仿真验证成功后,使用Verilog语言对BPSK调制解调算法进行了硬件描述,并对该算法进行了功能仿真。仿真结果证明了 BPSK调制解调算法在FPGA中的正确实现。最后对水声通信试验平台中的上位机进行了简单设计,并完成了与FPGA的相互数据通信。为了进一步验证所编写的FPGA算法的正确性能,进行了相应的水池试验验证。结果表明,由于Costas环能够正确补偿信号传输过程中所产生的频偏,Gardner环也可以补偿信号在传输过程中所产生的定时偏差,因此当收发通信距离较短、信道的多途影响较小时,通过对估计的码元符号和原始码元符号进行对比,计算出环路在同步后的数据误码率为0,星座图分布良好,验证了基于FPGA的BPSK调制解调算法的正确实现。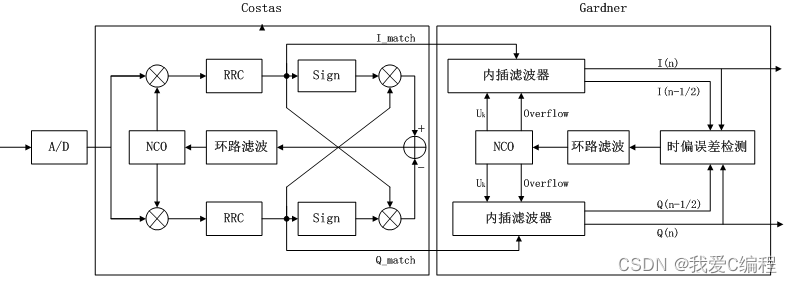

Costas环（Costas Loop）用在抑制载波调制信号（比如双边带抑制载波调制）和相位调制信号（BPSK、QPSK）的相干解调中的载波恢复（carrier frequency recovery）上。由通用电气公司的John P. Costas 在1950s发明。它的发明被描述为对现代数字通信产生了深远的影响。Costas环的主要应用是在无线通信接收机中。与基于PLL的检波器相比，它的优势在于，在相位差比较小的情况下，Costas环输出的误差电压为 sin(2(θi−θf)) ，而基于PLL的检波器输出的误差电压为 sin(θi−θf) ，这不仅使灵敏度提高了一倍，而且使Costas环路特别适合跟踪载波的多普勒频移，特别是在OFDM和GPS接收机中。

Gardner定时误差算法通常用在BPSK、QPSK信号，通过改进可以应用在QAM等多进制基带信号中。Gardner定时误差算法，该算法的一个特点是每个符号只需要使用两个采样点，一个是strobe点，即最佳观察点，另外一个是midstrobe点，即两个观察点之间的采样点。Gardener环中的数控振荡器与锁相环路中的NCO功能完全不同，这里的NCO作用是产生时钟，即确定内插基点mk，同时完成分数间隔uk的计算，以提供给内插器进行内插。
位同步环路中的数控振荡器（NCO）是一个相位递减器，它的差分方程为：
η(m+1)=[η(m)-ω(m)]mod1

式中，η(m)是第m个工作时钟NCO寄存器的内容，ω(m)为NCO的控制字，两者都是正小数。NCO的工作周期是T s(采样周期)，内插器的周期为T i，ω(m)由环路滤波器进行调节，使NCO在最佳采样时刻溢出。当环路达到平衡时，ω(m)近似是个常数，此时平均每隔1/ω(m)个采样周期，NCO就溢出一次，所以

gardner环内部结构如下所示：

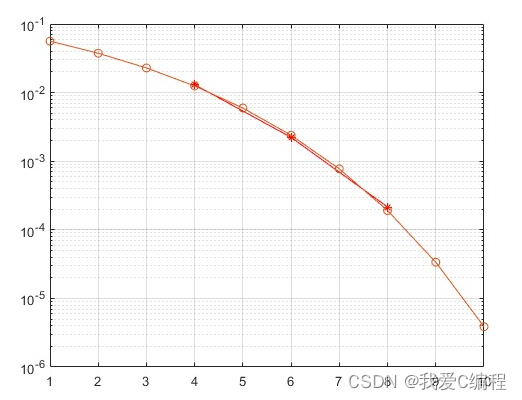
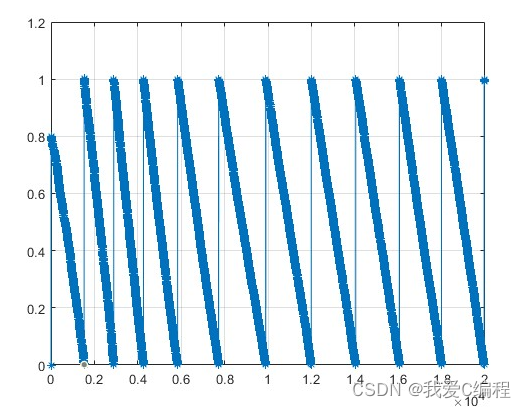
2.matlab算法仿真效果

matlab2022a仿真结果如下：

3.MATLAB核心程序

     mul = 2;%按块进入根升余弦滤波器
     for i = 1 + mul:carlen - mul
         %为加快收敛，前端使用较大的系数以快速震荡
         if i < 1000
                C1 = 0.007;
                C2 = C1 * 0.007;
         else
                C1 = 0.0005;
                C2 = C1 * 0.001;
         end
         %频率锁相环
         for k = 1 : nsamp
            I_NCO = cos(wc_nco/Freq_Sample*((i-1-mul)*nsamp+1 : (i-1+mul)*nsamp+nsamp)+mod(NCO_Phase,2*pi));%NCO产生的I路输入信息数据
            Q_NCO = - sin(wc_nco/Freq_Sample*((i-1-mul)*nsamp+1 : (i-1+mul)*nsamp+nsamp)+mod(NCO_Phase,2*pi));%NCO产生的Q路输入信息数据 
            I_RECE=rece((i-1-mul)*nsamp+1 : (i-1+mul)*nsamp+nsamp).*I_NCO;   %I路输入信息数据
            Q_RECE=rece((i-1-mul)*nsamp+1 : (i-1+mul)*nsamp+nsamp).*Q_NCO;   %Q路输入信息数据
            %根升余弦滤波
            I_RRC_S = RRCrece(I_RECE,Freq_Data,nsamp,alpha,delay);%I路输入信息数据经过根升余弦匹配滤波
            Q_RRC_S = RRCrece(Q_RECE,Freq_Data,nsamp,alpha,delay);%Q路输入信息数据经过根升余弦匹配滤波
            
            I_PLL=I_RRC_S(delay*nsamp-nsamp/2+mul*nsamp+2+k);   %鉴相器的I路输入信息数据
            Q_PLL=Q_RRC_S(delay*nsamp-nsamp/2+mul*nsamp+2+k);   %鉴相器的Q路输入信息数据
            dataoutI((i-1)*nsamp+k) = I_PLL;%用来查看鉴相器的I路输入信息数据
            dataoutQ((i-1)*nsamp+k) = Q_PLL;
            %鉴相器处理
            Discriminator_Out = (sign(I_PLL)*Q_PLL-sign(Q_PLL)*I_PLL)/sqrt(2);   
            dd((i-1)*nsamp+k) = Discriminator_Out;%用来查看鉴相器的输出
            %环路滤波器处理
            PLL_Phase_Part((i-1)*nsamp+k) = Discriminator_Out * C1;   
            Freq_Control((i-1)*nsamp+k) = PLL_Phase_Part((i-1)*nsamp+k)+PLL_Freq_Part((i-1)*nsamp+k-1);
            PLL_Freq_Part((i-1)*nsamp+k) = Discriminator_Out * C2 + PLL_Freq_Part((i-1)*nsamp+k-1);
            NCO_Phase = NCO_Phase + Freq_Control((i-1)*nsamp+k);  %生成的相位
            WC_frame((i-1)*nsamp+k) = FC_NCO + PLL_Freq_Part((i-1)*nsamp+k) * Freq_Sample;
            
            %=========================================================
            NCO_Phase_((i-1)*nsamp+k)=mod(NCO_Phase,2*pi);
         end
     end
A78