一、线特征提取

1.1 模板检测

使用模板在一幅图像上移动，他会对特定方向上的（一个像素宽）线响应强烈。下面是常见检测模板：

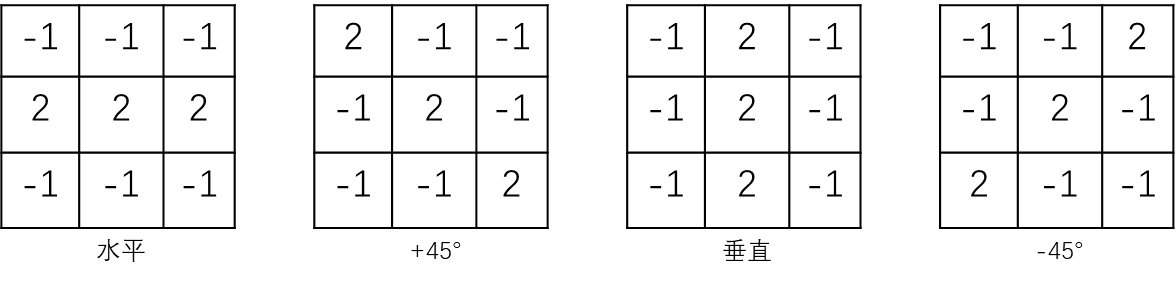
1.2 边缘检测

边缘检测的基本思想是使用如下两个准则之一找到图像中快速变换的位置：
1. 寻找灰度的一阶导数的幅值大于某个阈值的位置
2. 寻找灰度的二阶导数有零交叉的位置

matlab提供的函数：[g,t]=edge(f,'method',paramters)

1.2.1 Sobel边缘检测器

检测器模板：

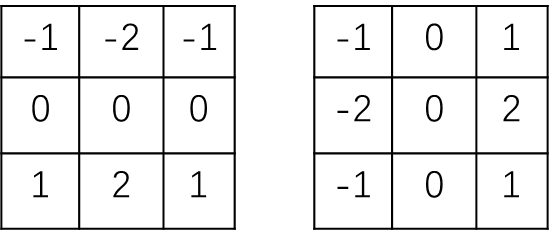
matlab函数：[g,t]=edge(f,'sobel',T,dir)

1.2.2 Prewitt边缘检测器

检测器模板：

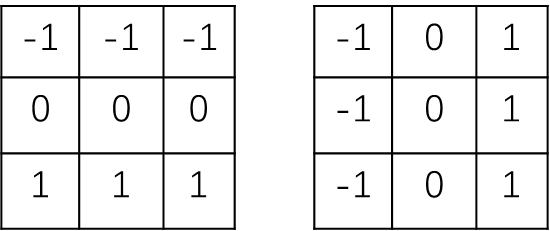
matlab函数：[g,t]=edge(f,'prewitt',T,dir)

1.2.3 Roberts边缘检测器

检测器模板：

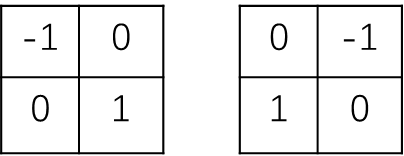
matlab函数：[g,t]=edge(f,'roberts',T,dir)

1.2.4 LoG检测器

介绍： 使用高斯函数的二阶导数，称为高斯拉普拉斯算子（LoG）。

检测原理: 使用${△}^{2}G(x,y)$对图像卷积有两个效果：它平滑了图像（降低了噪声），并计算拉普拉斯算子，进而产生一幅双边缘图像。然后通过查找双边缘之间的零交叉来定位边缘。

matlab函数：[g,t]=edge(f,'log',T,sigma)，T设置为0会产生封闭轮廓

1.2.5 零交叉检测器

与LoG方法相同的概念，但卷积是使用一个特定的滤波器函数H来完成。

matlab函数：[g,t]=edge(f,'zerocross',T,H)

1.2.6 Canny边缘检测器

是函数edge中最强大的边缘检测器。

matlab函数：[g,t]=edge(f,'canny',T,sigma)

1.3 霍夫变换（Hough）线检测

基本思想： 假设在X-Y平面有直线$y=kx+b$，该直线上的点$P_i$应满足该式子，反之如果一些点$P_i$满足该式子它们就在同一条直线上。利用霍夫变换，将该直线方程转换为$b=-kx+y$，那么在K-B平面（参数空间）上，这些点$P_i$都是一条直线，且相交于$(k,b)$，找到$(k,b)$即得到了X-Y平面的直线方程。

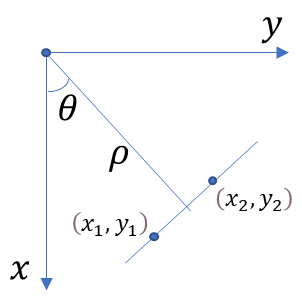
在实际的检测中，由于直线斜率k有可能为无穷大，所以用法线来表示直线$x\cos \theta +y\sin \theta =\rho$

算法步骤：

1. 使用canny算子检测图像边缘，得到二值化的边缘图像
2. 检测非背景点$(x,y)$【非0的点】作为参数带入：$x\cos \theta +y\sin \theta =\rho$，在累加单元$\theta \rho$(二维数组)将满足的$(\theta ,\rho )$元素值加1
3. 设定阈值，累加单元中大于阈值的参数$({\theta }_i,{\rho }_j)$即认为是X-Y平面上的直线
4. 画出直线$x\cos {\theta }_i+y\sin \theta ={\rho }_j$

matlab相关函数：
[H,theta,rho]=hough(f)
peaks = houghpeaks(H,NumPeaks)
lines=houghlines(f,theta,rho,peaks)

1.4 LSD算法

LSD（Rafael Grompone von Gioi, LSD: a Line Segment Detector，2010）是一种直线检测分割算法，它能在线性的时间内得出亚像素级精度的检测结果。该算法被设计成可以在任何数字图像上都无需参数调节。

缺点：
1、对于直线相交情况，若有相交必有至少一条直线被割裂为两条。又因为其基于梯度，直线交点梯度值往往又较小（不被检测为边缘点），因此很有可能相交的两条直线在交点处被割裂为四条线段；
2、由于局部检测算法自增长的特点，对于长线段被遮挡、局部模糊等原因经常割裂为多条直线。

【论文及代码】http://www.ipol.im/pub/art/2012/gjmr-lsd/

【GitHub】利用OpenCV和MATLAB进行封装代码

1.5 LBD算法

来源论文：《An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency，2013》

优势：该文章提出了LBD线检测算法，克服了LSD线检测碎片化问题和提高大尺度变化的性能，同时提出一种线特征匹配算法。

算法流程参考：https://www.cnblogs.com/Jessica-jie/p/7523364.html