现在有一个这样的问题需要求解
题目要求:给定一个n个元素的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1
示例
输入: nums= [-1,0,3,5,9,12] target= 9 输出: 4 解释: 9 出现在 nums中并且下标为 4
输入: nums= [-1,0,3,5,9,12], target= 2 输出: -1 解释: 2 不存在 nums中因此返回 -1
继上次写完二分查找后,又在网上查看了其他资料,发现二分查找其实常用的有两种写法,这篇文章里(二分查找)只写了一种形式,而且可能介绍的不是很详细,所以这里将二分查找的两种形式做以归纳总结,方便记忆。
二分查找的两种形式的主要区别在于区间的定义,①左闭右闭[left,right],②左闭右开[left,right)
具体来说就是下面这两种表示区间的方式,虽然表现方式略有差异,但实际上表达的区间范围是一致的,殊途同归(相信大家对初中数学开闭区间的描述仍有印象)

由于区间定义的微小差别,导致程序中mid变量的取值也有相应的改变(一定得改变,不然就会出错),下面我们来介绍一下这两种形式
①左闭右闭[left,right]
我们定义target是在一个左闭右闭[left,right]的区间里,那么要注意两个事情
- while的循环条件;while(left<=right)。在while的循环条件里面就要用<= ,因为这个时候left==right是有意义的
- if(nums[mid]>target)之后对right怎样处理?right要赋值为mid-1,因为当前这个nums[mid]一定不是target,那么接下来要查找的左区间的右边界就是mid-1
具体怎么写呢?
class Solution {
public:
int search(vector<int>& nums, int target) {
int left=0,right=nums.size()-1;
while(left<=right)
{
int mid=(right-left)/2+left;
if(nums[mid]==target)
{
return mid;
}
else if(nums[mid]>target)
{
right=mid-1;
}
else
{
left=mid+1;
}
}
return -1;
}
};对上面的程序做简单注释
int left=0,right=nums.size()-1;定义一个区间,左边界left=0,右边界right=nums.size()-1,实际上就是说定义了一个闭区间,要求包括整个数组的所有元素。定义target在这个区间范围里。
注意代码right=nums.size()-1,为什么要减1?因为nums.size()返回的是nums中有多少个元素,而我们又知道数组的下标是从0开始的,所以一个数组的最后一个元素的下标一定是这个数组中拥有元素的个数减1

while(left<=right)这里为什么要写成<=号,我们之前也说过,因为当left==right时,仍然是有意义的。
int mid=(right-left)/2+left;这里为什么要把mid写成这样?其实它和
int mid = (left+rirht)/2是一样的,那为什么要那样写而不写成下面这样,主要原因是怕内存溢出,
int类型的整数能够表示的最大数字是2147483647 ,假如在运行过程中,left不断逼近right,直到left和right两个数都接近2147483647,他们两个再相加结果就会溢出,会变成负数,所以改用mid=(right-left)/2+left
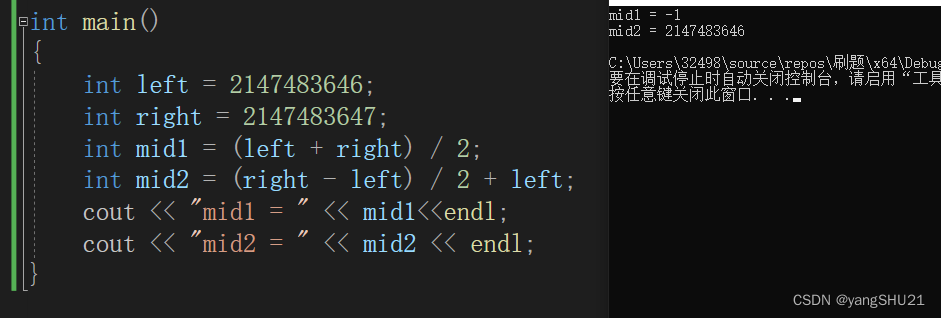
通过上面这个小测试我们就可以想通为什么要写成 mid=(right-left)/2+left的样子了。
在这里可能大家还会碰到另外一种书写形式
int mid=((right-left)>>1)+left这里的“>>"运算符是右移运算符,
举个例子
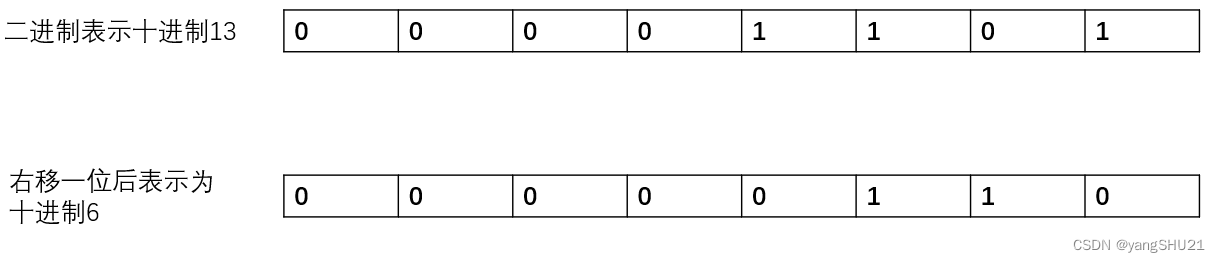

所以我们可以知道 int mid=((right-left)>>1)+left 和 int mid=(right-left)/2+left; 这两种形式是等效的,但是位运算符>>比’ / ‘快一些。因为位运算符直接对内存数据进行操作,不需要转成十进制,因此处理速度快;
if(nums[mid]==target)
{
return mid;
}这句代码应该很好理解,当nums[mid]==target,就是说如果mid位置处的值恰好等于我们要找的target,那直接返回mid就可以了,后面的缩小区间再查找就不用执行了,因为数组是升序的而且元素不重复,说明只有一个位置处的值等于target
else if(nums[mid]>target)
{
right=mid-1;
}这句就是说target在原区间的左半边,所以新区间的范围是[left,mid-1]
else
{
left=mid+1;
}这句就是说target在原区间的右半边,所以新区间的范围是[mid+1,right]
while循环之外就是说 在数组中没有找到target,就返回-1;
②左闭右开[left,right)
如果定义target在左闭右开的区间里,[left,right),那么边界处理问题就会发生变化,要注意这一点,否则就会出错
- while(left<rigth),注意这里使用的是<,因为left==right在区间[left,right)是没有意义的
- if(nums[mid]>target),right=mid,因为当前nums[mid]不等于target,去左区间继续寻找,但是这时候由于区间是左闭右开的,所以right更新为mid,
核心代码如下
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while (left < right)
{
int mid = (right - left) / 2 + left;
if (nums[mid] == target)
{
return mid;
}
else if (nums[mid] > target)
{
right = mid;
}
else
{
left = mid + 1;
}
}
return -1;
}这里就不给大家逐句讲解了,唯一需要注意的就是
else if (nums[mid] > target)
{
right = mid;
}这里涉及到右区间的处理问题,大家注意一下。
接下来我们把两种形式的代码放在vs里面测试一下
#include<iostream>
#include<vector>
using namespace std;
①[left,right]
//int search(vector<int>& nums, int target) {
// int left = 0, right = nums.size() - 1;
// while (left <= right)
// {
// int mid = (right - left) / 2 + left;
// if (nums[mid] == target)
// {
// return mid;
// }
// else if (nums[mid] > target)
// {
// right = mid - 1;
// }
// else
// {
// left = mid + 1;
// }
// }
// return -1;
// }
//②[left,right)
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while (left < right)
{
int mid = (right - left) / 2 + left;
if (nums[mid] == target)
{
return mid;
}
else if (nums[mid] > target)
{
right = mid;
}
else
{
left = mid + 1;
}
}
return -1;
}
int main()
{
vector<int> vec{ 1,4,5,7,11,14,18 };
cout << "vec: ";
for (auto c : vec)
{
cout << c << " ";
}
cout << endl;
int tar = 5;
/* int tar = 2;*/
int i=search(vec, tar);
if (i >= 0)
cout << tar<<" index is " << i << endl;
else
cout << tar<<" not found" << endl;
}程序运行结果如下,