392.判断子序列

思路：

1.确定dp数组（dp table）以及下标的含义:

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

2.确定递推公式：

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了,dp[i][j] = dp[i - 1][j - 1] + 1
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

3.dp数组如何初始化：

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

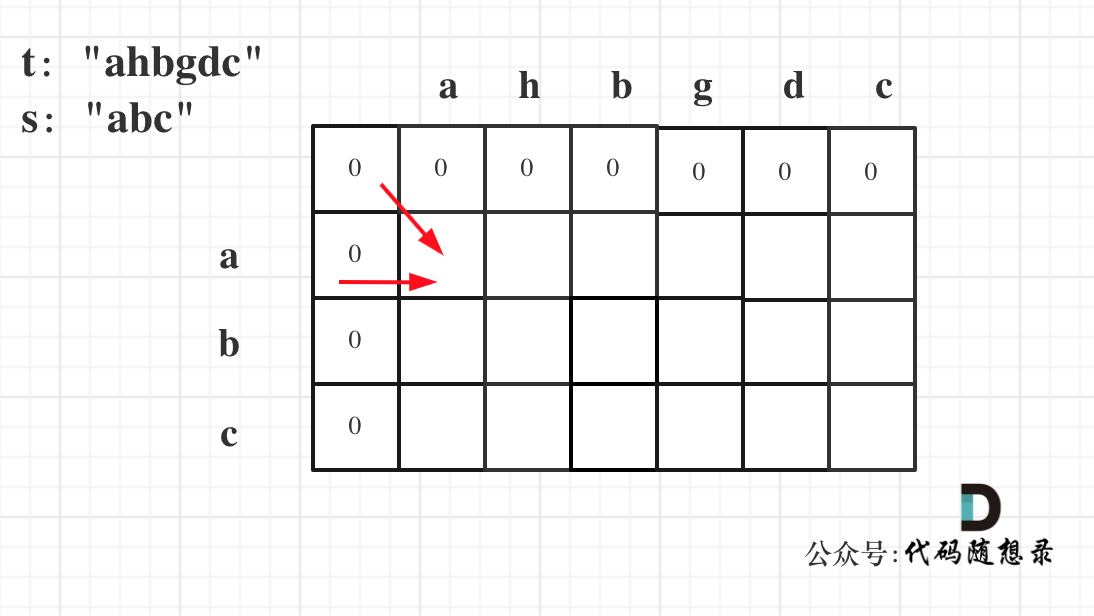
392.判断子序列

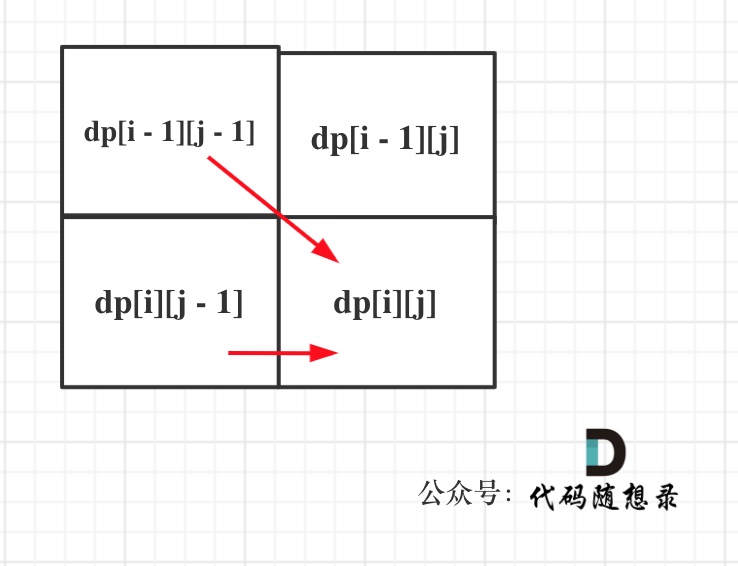
4.遍历顺序

同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1][j - 1]，那么遍历顺序也应该是从上到下，从左到右

如图所示：

392.判断子序列1

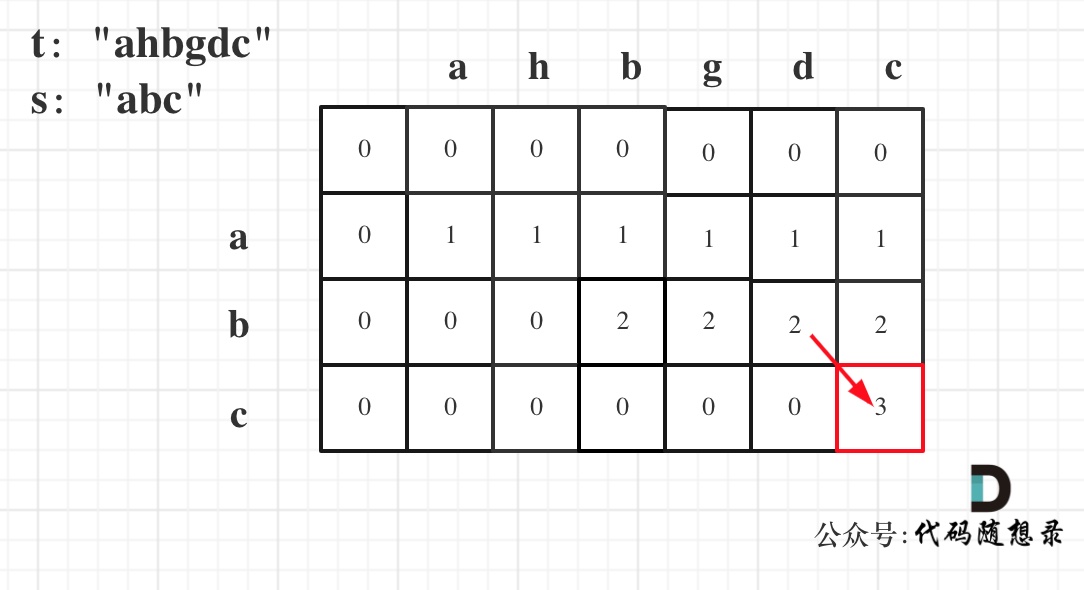
5.举例推导dp数组

以示例一为例，输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下：

392.判断子序列2

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        size1 = len(s)
        size2 = len(t)
        if size1 > size2:
            return False

        dp =  [[0]* (size2+1) for _ in range(size1+1)]

        for i in range(1,size1+1):
            for j in range(1,size2+1):
                if (s[i-1] == t[j-1]):
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = dp[i][j-1]
        return dp[-1][-1] == len(s)

115.不同的子序列

思路：

1.确定dp数组（dp table）以及下标的含义：dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

2.递推公式：

if (s[i - 1] == t[j - 1])
- dp[i][j]可以有两部分组
- 一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]
- 一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]
- e.g: s：bagg 和 t：bag ，s[3] 和t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。
  
  所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
if (s[i - 1] != t[j - 1])
- 只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素）即：dp[i][j] = dp[i][j - 1];

3.初始化：

dp[i][0] 表示以 i - 1 为结尾的 s 子序列中出现空字符串的个数。把 s 中的元素全删除，出现空字符串的个数就是 1，则 dp[i][0] = 1。
dp[0][j] 表示空字符串中出现以 j - 1 结尾的 t 的个数，空字符串无论怎么变都不会变成 t，则 dp[0][j] = 0
dp[0][0] 表示空字符串中出现空字符串的个数，这个应该是 1，即 dp[0][0] = 1。

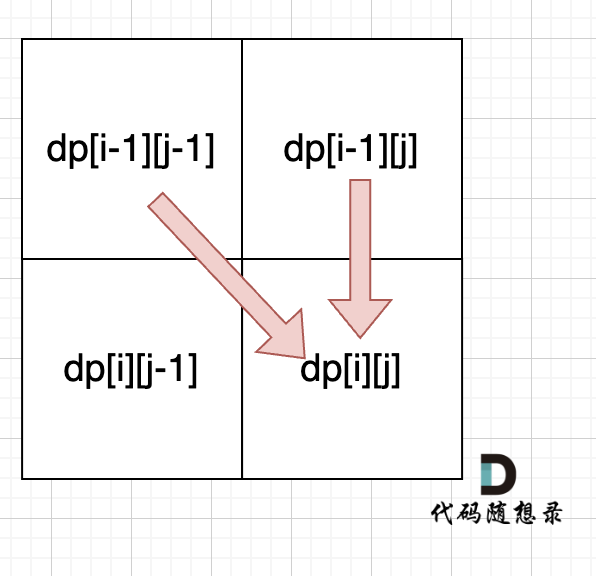
4.确定遍历顺序

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] 和dp[i][j] = dp[i][j - 1] 中可以看出dp[i][j]都是根据左上方和正上方推出来的。从上到下，从左到右

5.举例推导dp数组

以s：“baegg”，t："bag"为例，推导dp数组状态如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fG53RlwB-1683555981910)(https://code-thinking.cdn.bcebos.com/pics/115.%E4%B8%8D%E5%90%8C%E7%9A%84%E5%AD%90%E5%BA%8F%E5%88%97.jpg)]

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        sizes = len(s)
        sizet = len(t)
        if sizet > sizes:
            return 0
        dp = [[0] *(sizet+1) for _ in range(sizes+1)]
        for i in range(sizes):
            dp[i][0] = 1
        for i in range(1,sizes+1):
            for j in range(1,sizet+1):
                if (s[i-1]==t[j-1]):
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]