文章目录
- 第一节:逻辑结构与存储结构
- 1. 逻辑结构
- 2. 存储结构
- 1. 顺序存储
- 2. 链式存储
- 3. 顺序存储与链式存储分析
- 第二节:算法的评价(时间复杂度与空间复杂度)
- 1. 算法定义
- 2. 时间复杂度
- 3. 空间复杂度
第一节:逻辑结构与存储结构
两者对比
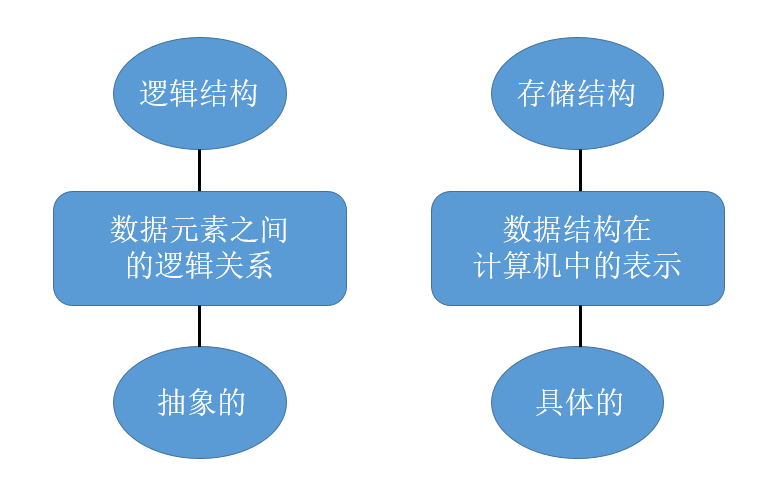
1. 逻辑结构

2. 存储结构
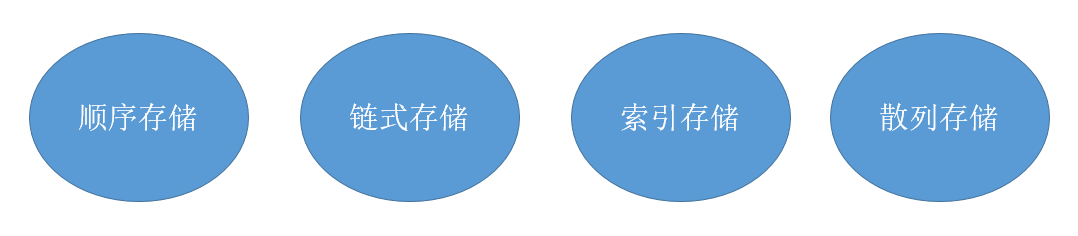
说明:存储结构有四种,但是最终的存储方式只有顺序存储和链式存储两种。
1. 顺序存储
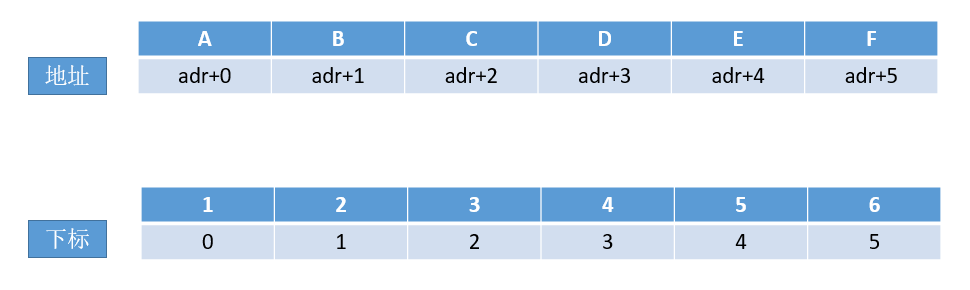
int array[6]={1,2,3,4,5,6}; // 定义数组并初始化
printf{"%d\n",array[3]}; // 随机访问第4个元素
说明:地址相当于指针取值。下标相当于随机访问。
2. 链式存储
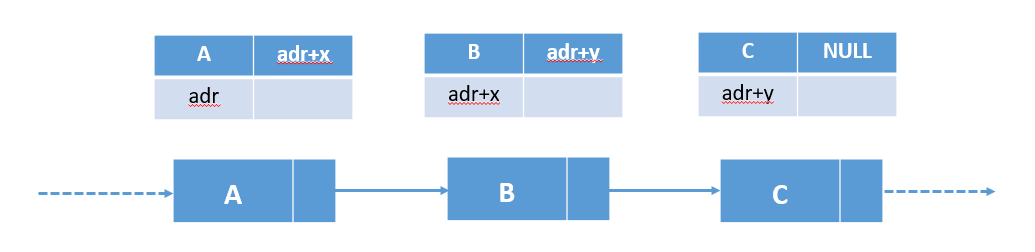
说明:前一个节点存放下一节点的指针。
// 仅做示例,无法运行
Typdef struct Lnode{
ElemType data;
struct Lnode *next;
}Lnode,*LinkList;
Lnode *L;
L=(LinkList)malloc(sizeof(Lnode));
A->next=B;B->next=C;
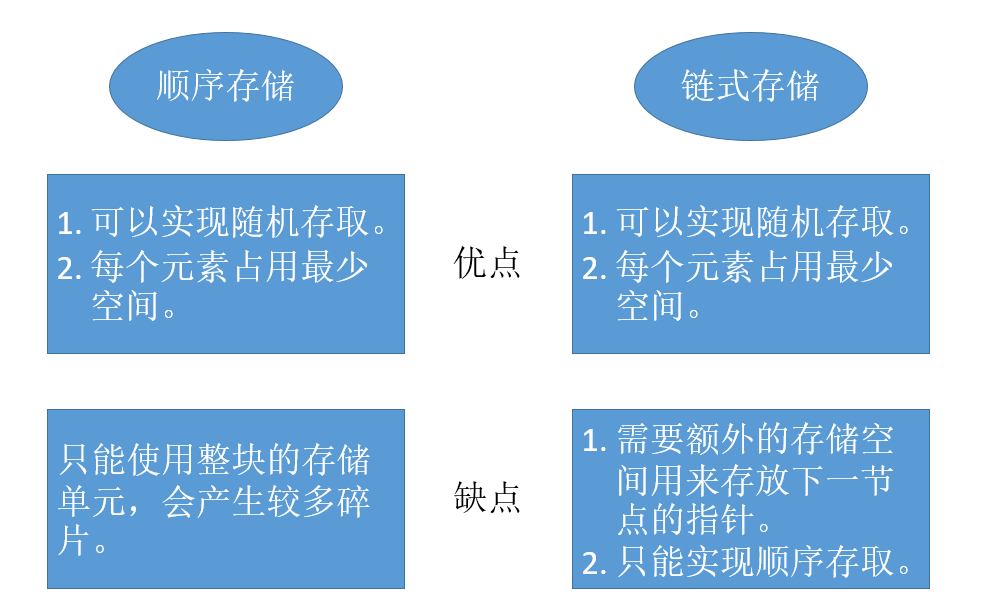
3. 顺序存储与链式存储分析
第二节:算法的评价(时间复杂度与空间复杂度)
1. 算法定义
算法定义是对特定问题求解步骤的描述。
一个基本算法包括:有穷、确定、可行、输入、输出。
2. 时间复杂度
时间复杂度是指算法中所有语句的频度(执行次数)之和。记为:
T(n)=O(f(n))
其中,n是问题的规模;f(n)是问题规模n的某个函数。
随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同(正相关)。
常见的时间复杂度:
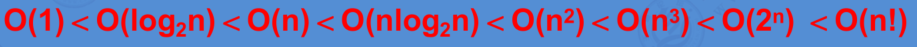
最高阶数越小,说明算法的时间性能越好。
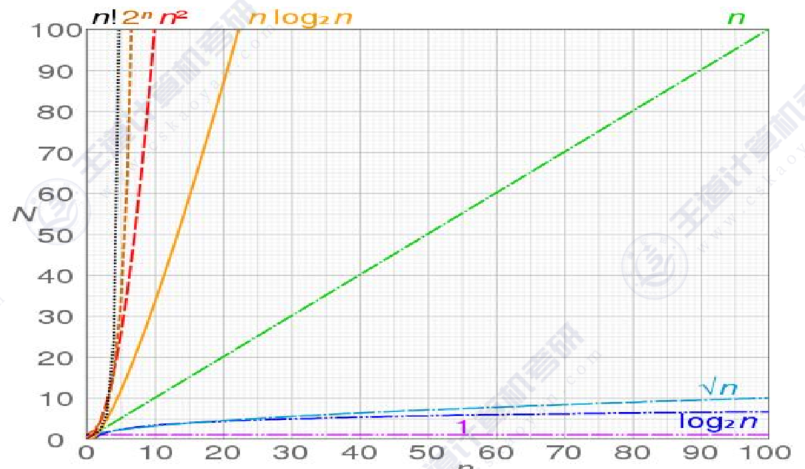
例题:






时间复杂度计算忽略高阶项系数和低阶项。
思考:如果一个算法的执行次数为3n^3+5n,那么该算法的时间复杂度是多少?
答案是O(n3),因为忽略了高阶项系数3,和低阶项5n,剩余n3。
3. 空间复杂度
空间复杂度S(n)指算法运行过程中所使用的辅助空间的大小。记为:
S(n)=O(f(n))
-
除了需要存储算法本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。
-
若输入数据所占空间只取决于问题本身,和算法无关,这样只需分析该算法在实现时所需的辅助单元即可。
-
算法原地工作是指算法所需的辅助空间是常量,即O(1)。

![[附源码]Python计算机毕业设计Django的玉石交易系统](https://img-blog.csdnimg.cn/2c117505bb3c439f8a6ecdfd6234c089.png)

![[附源码]计算机毕业设计SpringBoot计算机相关专业考研资料管理系统](https://img-blog.csdnimg.cn/ece30d73d864465ca71f7618c4542c2c.png)

![[附源码]SSM计算机毕业设计学术文献分享网站JAVA](https://img-blog.csdnimg.cn/052f1940a5a947d3a318aae00dda77cf.png)

![[附源码]Python计算机毕业设计Django的物品交换平台](https://img-blog.csdnimg.cn/ae690f09ab264cde9e5b384c81ea8331.png)




