拓扑排序算法

news2024/11/26 10:28:01

背景

拓扑排序是啥意思？

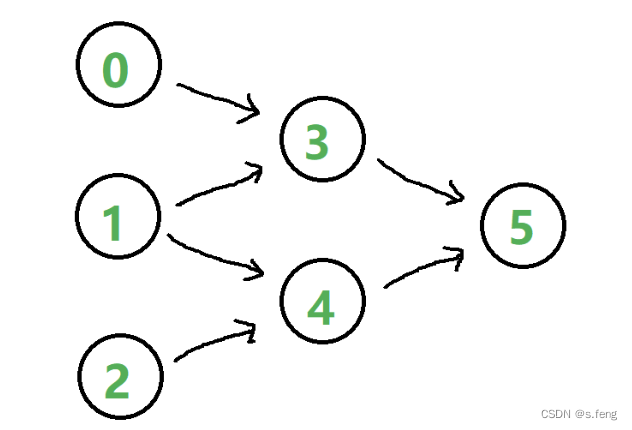
拓扑排序是指: 将有向无环图(DAG)展开为一维的执行序列。DAG顾名思义就是有方向的图，下面这张图就简单说明了啥是有向无环图。一般人可能用到这个算法的情况不多，但是刷leetcode的课程表问题肯定遇到过，其次搞人工智能的同学静态图执行顺序也不应该陌生。

算法流程

先简单分析，从上面的图可以知道，要执行3节点，依赖0，1，所以需要先执行完0，1。依次类推可以有一下的执行顺序：

[0,1,2,3,4,5]
[0,2,1,3,4,5]
[0,1,2,4,3,5]

此外还有很多排序方式，可见拓扑图的排序有很多选择，只要满足执行依赖要求都是可行的拓扑排序。接下来正式分析一下算法流程：

入度数组：这里需要增加两个概念：入度和出度，入度是指该节点有几个输入，出度是指该节点有几个输出。根据上面的铺垫可以很容易想到，入度为0的节点当下是可以执行的，毕竟他没有什么依赖。所以我们可以搞一个入度数组，记录每个节点的入度个数，如果当下的入度个数为0，那么该节点就是当下可以执行。
邻接表：根据上面的图我们知道，当0，1节点执行完后，节点2的入度也就变成0了，所以每个节点执行完，都应该更新一波入度数组，那么怎么更新了？这就依赖邻接表来完成，这里邻接表是一个map<node, vector<node>>，其中key是节点名node，value是依赖该key_node的节点们，也就是说把key_node作为入度之一的节点。

代码

//入度数组
vector<int> TopologyDfsSort(graph)
{
	vector<int> in_degree(n,0);
	init(in_degree, graph);
	//邻接表
	unordered_map<int, vector<int>> map;
	init(map, graph);
	//当下可执行的节点集合
	vector<int> res;
	// 每次跟新的队列
	queue<int> q;
	for(int i=0; i<in_degree.size(); i++)
	{
		if(in_degree[i]==0) 
		{
			q.push(i);//入度为0的都可以执行
			res.push(i);//入度为0的都可以执行
		}
	}
	//更新
	while(!q.empty())
	{
		//一轮执行size个节点，q中是表示该轮可以执行的节点
		int size = q.size();
		for(int i=0; i<size; i++)
		{
			int exec_node = q.front();
			q.pop();
			//一旦exec_node执行，那么依赖exec_node的node的入度值都可以减一
			vector<int> nodes = map[exec_node];
			for(auto id:nodes)
			{
				in_degree[id]--;
				if(in_degree[id]==0)//如果入度为0，那么就可以进入下一轮执行
				{
					q.push(id);//入度为0的都可以执行
					res.push(id);//入度为0的都可以执行
				}
			}
		}
	}
	return res;
}