题目及测试

package pid040;
/* 40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。 

 

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
 

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
*/

import java.util.List;

public class main {
	
	public static void main(String[] args) {
		int[][] testTable = {{10,1,2,7,6,1,5},{2,5,2,1,2}};
		int[] testTable2={8,5};
		for (int i=0;i<testTable.length;i++) {
			test(testTable[i],testTable2[i]);
		}
	}
		 
	private static void test(int[] ito,int ito2) {
		List<List<Integer>> rtn;
		Solution solution=new Solution();
		long begin = System.currentTimeMillis();
		for (int i = 0; i < ito.length; i++) {
		    System.out.print(ito[i]+" ");		    
		}
		System.out.println();
		//开始时打印数组
		System.out.println("ito2="+ito2);
		rtn = solution.combinationSum2(ito,ito2);//执行程序
		long end = System.currentTimeMillis();	
		
		System.out.println( "rtn=" );
		for(int i=0;i<rtn.size();i++){
			for(int j=0;j<rtn.get(i).size();j++){
				System.out.print( rtn.get(i).get(j)+"  ");
			}		
			System.out.println();
		}
		
		System.out.println();
		System.out.println("耗时：" + (end - begin) + "ms");
		System.out.println("-------------------");
	}

}

没想出来

解法1（别人的）

与第 39 题（组合之和）的差别

这道题与上一问的区别在于：

第 39 题：candidates 中的数字可以无限制重复被选取；

第 40 题：candidates 中的每个数字在每个组合中只能使用一次。

相同点是：相同数字列表的不同排列视为一个结果。

如何去掉重复的集合（重点）

为了使得解集不包含重复的组合。有以下 22 种方案：

使用 哈希表 天然的去重功能，但是编码相对复杂；

这里我们使用和第 39 题和第 15 题（三数之和）类似的思路：不重复就需要按 顺序 搜索， 在搜索的过程中检测分支是否会出现重复结果 。注意：这里的顺序不仅仅指数组 candidates 有序，还指按照一定顺序搜索结果。

 

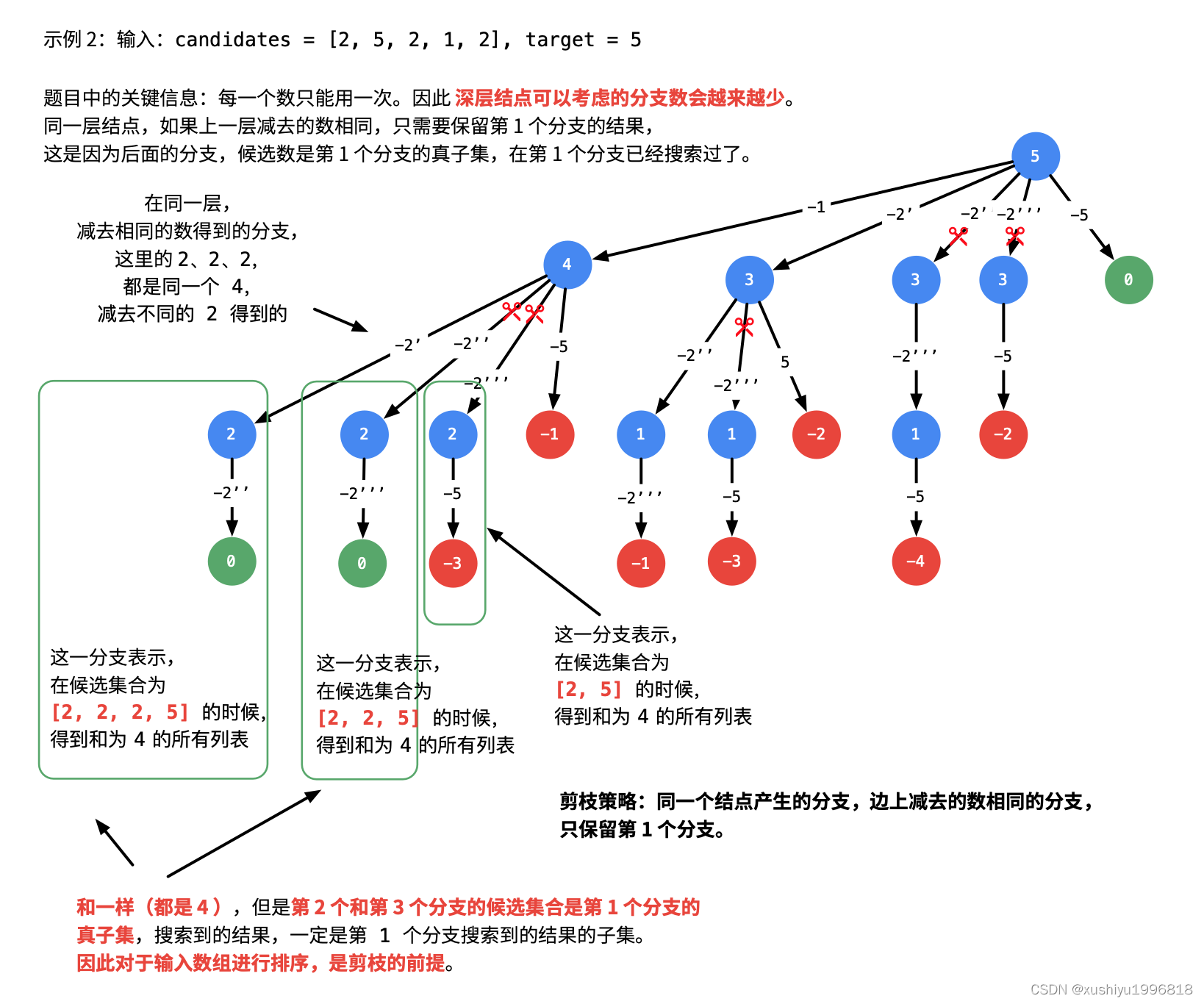
由第 39 题我们知道，数组 candidates 有序，也是 深度优先遍历 过程中实现「剪枝」的前提。
将数组先排序的思路来自于这个问题：去掉一个数组中重复的元素。很容易想到的方案是：先对数组 升序 排序，重复的元素一定不是排好序以后相同的连续数组区域的第 11 个元素。也就是说，剪枝发生在：同一层数值相同的结点第 22、33 ... 个结点，因为数值相同的第 11 个结点已经搜索出了包含了这个数值的全部结果，同一层的其它结点，候选数的个数更少，搜索出的结果一定不会比第 11 个结点更多，并且是第 11 个结点的子集。（说明：这段文字很拗口，大家可以结合具体例子，在纸上写写画画进行理解。）

说明：

解决这个问题可能需要解决 第 15 题（三数之和）、 第 47 题（全排列 II）、 第 39 题（组合之和）的经验；

对于如何去重还不太清楚的朋友，可以参考当前题解的 高赞置顶评论 。

解释语句: if cur > begin and candidates[cur-1] == candidates[cur] 是如何避免重复的。

这个避免重复当思想是在是太重要了。
这个方法最重要的作用是，可以让同一层级，不出现相同的元素。即
                  1
                 / \
                2   2  这种情况不会发生 但是却允许了不同层级之间的重复即：
               /     \
              5       5
                例2
                  1
                 /
                2      这种情况确是允许的
               /
              2  
                
为何会有这种神奇的效果呢？
首先 cur-1 == cur 是用于判定当前元素是否和之前元素相同的语句。这个语句就能砍掉例1。
可是问题来了，如果把所有当前与之前一个元素相同的都砍掉，那么例二的情况也会消失。 
因为当第二个2出现的时候，他就和前一个2相同了。
                
那么如何保留例2呢？
那么就用cur > begin 来避免这种情况，你发现例1中的两个2是处在同一个层级上的，
例2的两个2是处在不同层级上的。
在一个for循环中，所有被遍历到的数都是属于一个层级的。我们要让一个层级中，
必须出现且只出现一个2，那么就放过第一个出现重复的2，但不放过后面出现的2。
第一个出现的2的特点就是 cur == begin. 第二个出现的2 特点是cur > begin.

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        int len = candidates.length;
        //数组一定要时有序的，才能进行深度递归
        Arrays.sort(candidates);
        //深度递归
        dfs(candidates, len, 0 , target, path, res);
        return res;
    }
    public void dfs(int[] candidates, int len, int dept, int target, Deque<Integer> path, List<List<Integer>> res){
        //如果递归到叶子结点，节点值刚好等于0，那说明路径上的元素就是结果
        if(target == 0){
            //将路径上的结果加入返回结果集上
            res.add(new ArrayList<>(path));
            //退出递归
            return; 
        }
        for(int i = dept;i< len; i++){
            //大剪枝，如果在有序的情况下，当前元素已经大于目标数组元素
            //那说明后面的元素就不在需要遍历，原因后面的元素比当前元素更大。
           if(target- candidates[i] < 0){
               break;
           }
           //小剪枝，发生在同层， 可以自己在图上画一个在第一个节点取1后的几种情况就可以发现
           //如果同层的元素的值，相同，就不在需要递归了，
           //原因在有序的情况下，后面出现的元素都会相同，造成结果集也会相同
           if(i> dept && candidates[i] == candidates[i-1]){
               continue;
           }
           //将数组的元素加入路径集合中
            path.addLast(candidates[i]);
            //进行深度递归下一层，所以i+1，
            //这边的重复，允许不同层重复，但是同层不能重复，
            dfs(candidates, len, i+1, target-candidates[i],path,res);
            //剪枝，将元素从末尾开始删除，
            //相当于将树，从叶子结点开始向根结点删除。
            path.removeLast();
          
        }
    }
}