目录
中国十大最具发展潜力城市
docker是什么?能介绍一下吗?
中国十大最具发展潜力城市
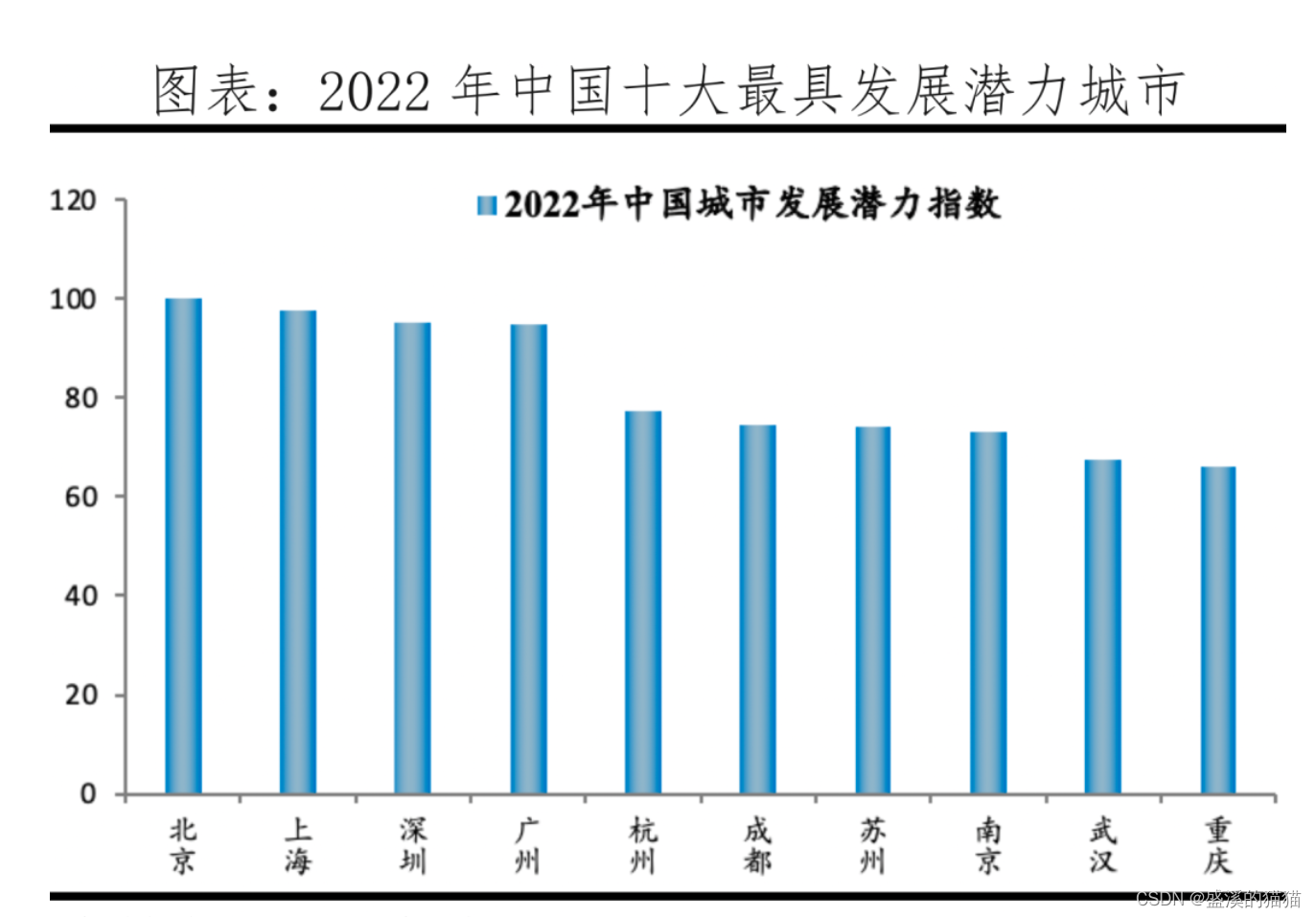
按照人随产业走、产业决定城市兴衰、规模经济和交通成本等区位因素决定产业布局的基本逻辑,我们在《中国城市发展潜力排名:2022》研究报告中对全国除港澳台外的337个地级及以上城市的发展潜力进行客观排名,北京、上海、深圳、广州、杭州、成都、苏州、南京、武汉、重庆位居前10名。
docker是什么?能介绍一下吗?
Docker是一种用于开发、交付和运行应用程序的开放平台。它使用操作系统级虚拟化来提供隔离环境,使得应用程序可以在各种不同的计算机上以轻量、可移植的容器形式运行。
Docker容器可以包含应用程序及其所有依赖项,从而可以实现一次打包,随处运行。Docker还提供了一组工具和服务,可以方便地创建、管理和部署容器,支持应用程序在多个环境中的移植性,并且可以大大加速开发和部署过程。
Docker在开发、测试、部署和运行应用程序方面具有广泛的应用,可以用于快速部署和扩展Web应用程序、处理大规模数据分析和处理任务、构建基于微服务架构的应用程序等。
简而言之,Docker 是一个可供开发者通过容器(container)来构建,运行和共享应用(application)的平台。用容器来部署应用被称为集装箱化(containerization)。
不是我说,docker真的好可爱,我真的很喜欢这个UI设计和美工