算法设计 || 实验一用分治法实现元素的归并与检索（头歌详解+本题分析笔记）

（一）递归与分治是个啥？

1.递归（归并排序）

2.分治（二分检索算法）

（二）头歌代码怎么写？

（三）代码部分详解：

（四）本题educoder平台要求是输入了10个数字，其实题目要求是随机生成20个数字，那么代码：

（五）一个小小报错的解决新路历程

鉴于最近看人家的超级好朋友每次写实验报告思考的那么认真，本人对自己囫囵吞枣的行为深感抱歉和惋惜，之后会励志当个有内涵的好孩子！

本文为Molly的原创内容，请勿转载!

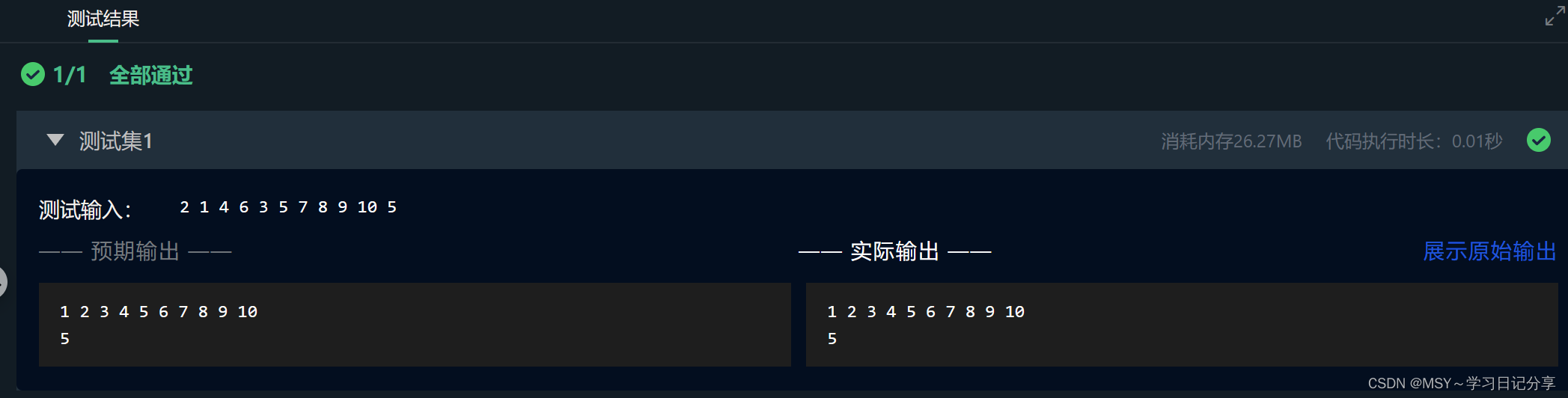
随机生成20个从1－100之间的随机数，用递归与分治法编程实现元素的查找算法。

（一）递归与分治是个啥？

1.递归（归并排序）

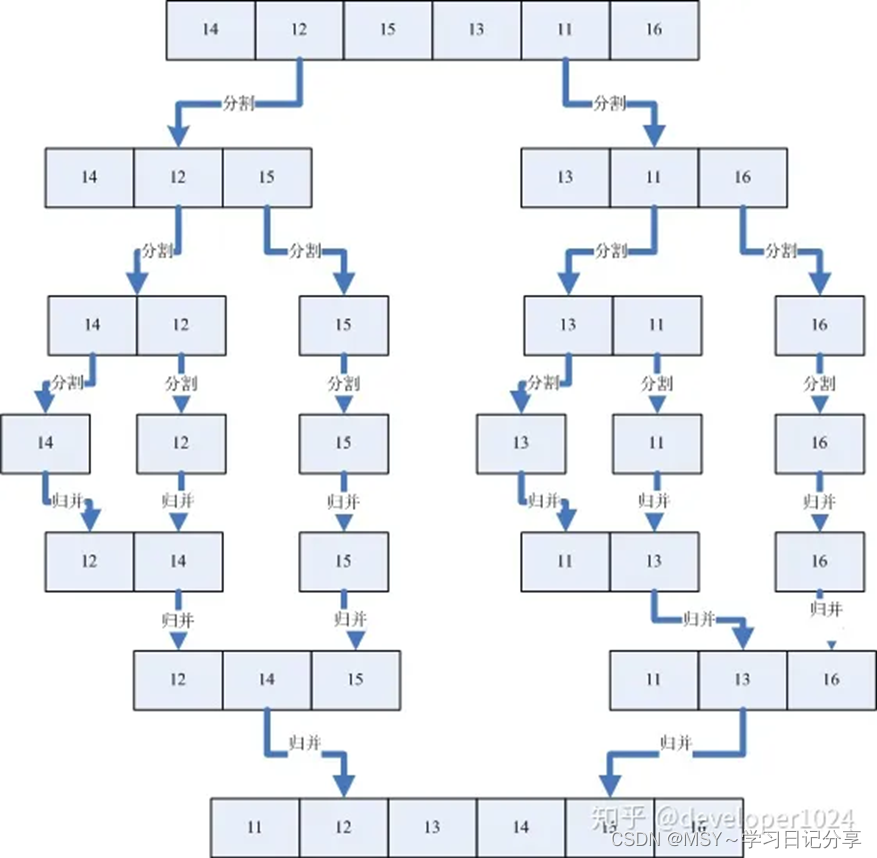
2.分治（二分检索算法）

大佬的笔记呈上：(222条消息) 二分搜索算法详解（Binary Search）_bfhonor的博客-CSDN博客

（二）头歌代码怎么写？

PS：这个代码可以借鉴的学习，但是觉得真的是特别冗长（注释希望可以帮助你理解）

/*
本关任务：随机生成20个从1－100之间的随机数，用递归与分治法编程实现元素的查找算法。
*/
//2100300805 毛姝垚
#include <stdlib.h>//标准函数库：常用函数定义（内存分配+随机数生成...）
#include <stdio.h>//标准输入输出库，主要包含标准输入输出函数的定义。
//#include <time.h>// 时间库，主要包含与时间有关的函数的定义
#define N 10//定义宏，将常量N设为10。
//合并函数：将a数组中p到mid，mid+1到r之间的数排序合并
void Merge(int a[],int p,int mid,int r)
{
    int result[r-p+1]; 定义一个数组result，长度为r-p+1。
    int k;//循环变量，当前遍历到的元素位置
    int i=p;//p:待排序数组的左边界
    int j=mid+1;
    // 将a数组中p到r之间的数复制到result数组中。
    /*目的是为了方便后续的归并操作，因为归并排序算法需要将待排序数组不断分割成若干个小数组，然后将这些小数组按照一定的顺序进行合并，而将待排序数组的一部分复制到新数组中就是为了方便后续的合并操作，避免在原数组中进行复杂的操作。*/
    for(k=p;k<=r;k++)
    {
        result[k-p]=a[k];//result[k-p]表示新数组result中第k-p个元素，a[k]表示待排序数组a中第k个元素。 
    }
    // 将result数组中的数按顺序赋值给a数组中p到r之间的数。（归并排序中合并操作）
    /*if-else语句来判断当前需要将哪个子数组中的元素放入合并后的结果数组a中。*/
    for(k=p;k<=r;++k){
        if(i>mid)//左侧已放入结果数组，只需放入右侧
        {
            a[k]=result[j-p];
            j++;
        }
        else if(j>r){//右半部分子数组中的元素已经全部放入了结果数组中，此时只需将左半部分子数组中尚未放入结果数组的元素依次放入即可
            a[k]=result[i-p];
            i++;
        }
        else if (result[i-p]>result[j-p])
        {
            a[k]=result[j-p];
            j++;
        }
        else//左半部分子数组中的第i个元素小于或等于右半部分子数组中的第j个元素
        {
            a[k]=result[i-p];
            i++;
        }
    }
}
// 归并排序函数，将a数组中p到r之间的数进行排序。
void Mergesort(int a[],int p,int r)
{
    int mid;
    if(p < r)
    {
        mid= (p + r) / 2; // 求出中间位置。
        // 递归调用Mergesort函数，将数组不断分为左右两部分进行排序。
        Mergesort(a, p , mid);
        Mergesort(a, mid + 1, r);
        // 将左右两部分合并排序。
        Merge(a, p , mid, r);
    }
}

// 二分查找函数，将a数组中p到r之间的数进行二分查找，寻找目标数target。
void search(int a[],int target,int p,int r)
{
    int mid =(p+r)/2; // 求出中间位置。
    if(target > a[mid]) // 如果目标数大于中间位置的数，则在右半部分查找。
    {
        p=mid+1;
    }
    if(target < a[mid]) // 如果目标数小于中间位置的数，则在左半部分查找。
    {
        r=mid-1;
    }
    if(target==a[mid]) // 如果目标数等于中间位置的数，则输出中间位置的数并返回。
    {
        printf("%d",a[mid]);
        return;
    }
    else // 否则递归调用serch函数，在左右两部分中继续查找。
    {
       search(a,target,p,r);
    }
}

int main(void)
{
    int a[21]; // 数组长度为N+1，为了避免输出后面的空格
    for(int i=0; i<10; ++i){
        scanf("%d",&a[i]); // 输入10个数
    }

    int target;
    scanf("%d",&target); // 输入目标数
    Mergesort(a, 0, 9); // 对数组进行归并排序

    int j=0;
    for(int j=0; j<N; ++j){
        printf("%d",a[j]); // 输出排序后的数组
        if(j < N-1) { // 判断是否为最后一个元素，如果不是，在元素后面加空格
            printf(" ");
        }
    }
    printf("\n");
    search(a, target, 0, 9); // 在排序后的数组中进行二分查找
    return 0;
}

（三）代码部分详解：

1. 将待排序的数组a中p到r范围内的元素复制到一个名为result的新数组中。其中，p表示待排序数组的左边界，r表示待排序数组的右边界，k为循环变量，result[k-p]表示新数组result中第k-p个元素，a[k]表示待排序数组a中第k个元素。举个例子，如果p=2，r=5，那么就是将待排序数组a中第2个元素到第5个元素（即a[2]到a[5]）复制到新数组result中，分别存储在result[0]、result[1]、result[2]、result[3]四个位置上。这样做的目的是为了方便后续的归并操作，因为归并排序算法需要将待排序数组不断分割成若干个小数组，然后将这些小数组按照一定的顺序进行合并，而将待排序数组的一部分复制到新数组中就是为了方便后续的合并操作，避免在原数组中进行复杂的操作。

2. if-else循环部分：

归并排序中的合并（merge）操作，将已经排好序的子数组合并成一个更大的有序数组。其中，p表示待合并数组的左边界，r表示待合并数组的右边界，mid表示待合并数组的中间位置，result是一个辅助数组，用于存放合并后的结果。具体的解释如下：首先，for循环遍历待合并数组中的所有元素。其中，变量k表示当前遍历到的元素位置。接着，代码使用了if-else语句来判断当前需要将哪个子数组中的元素放入合并后的结果数组a中。具体的判断逻辑如下：

如果i已经大于mid了，说明左半部分子数组中的元素已经全部放入了结果数组中，此时只需将右半部分子数组中尚未放入结果数组的元素依次放入即可。因此，将result数组中j-p位置的元素放入结果数组a的第k个位置中，并将j自增1，以便下一次循环。
如果j已经大于r了，说明右半部分子数组中的元素已经全部放入了结果数组中，此时只需将左半部分子数组中尚未放入结果数组的元素依次放入即可。因此，将result数组中i-p位置的元素放入结果数组a的第k个位置中，并将i自增1，以便下一次循环。
如果左半部分子数组中的第i个元素大于右半部分子数组中的第j个元素，说明应该将右半部分子数组中的第j个元素放入结果数组中，因为右半部分子数组中的元素已经排好序，且当前右半部分子数组中的第j个元素是所有右半部分子数组中尚未放入结果数组的元素中最小的一个。因此，将result数组中j-p位置的元素放入结果数组a的第k个位置中，并将j自增1，以便下一次循环。
如果左半部分子数组中的第i个元素小于或等于右半部分子数组中的第j个元素，说明应该将左半部分子数组中的第i个元素放入结果数组中，因为左半部分子数组中的元素已经排好序，且当前左半部分子数组中的第i个元素是所有左半部分子数组中尚未放入结果数组的元素中最小的一个。因此，将result数组中i-p位置的元素放入结果数组a的第k个位置中，并将i自增1，以便下一次循环。最后，当for循环结束时，结果数组a中就包含了待合并数组中所有元素，并且这些元素已经按从小到大的顺序排好了序。

（四）本题educoder平台要求是输入了10个数字，其实题目要求是随机生成20个数字，那么代码：

/*使用了两个函数来实现元素的查找算法，一个是递归实现的recursive_search函数，一个是分治法实现的divide_search函数。在主函数中，先随机生成20个1-100之间的整数，然后输入要查找的元素，最后调用recursive_search或divide_search函数进行查找，并输出查找结果。*/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_NUM 100  // 随机数的范围
#define NUM_COUNT 20  // 随机数的个数
// 递归实现元素查找算法
int recursive_search(int arr[], int left, int right, int target)
{
    if (left > right) {
        return -1;  // 查找失败，返回-1
    }
    int mid = left + (right - left) / 2;  // 计算中间位置
    if (arr[mid] == target) {
        return mid;  // 查找成功，返回元素下标
    } else if (arr[mid] < target) {
        return recursive_search(arr, mid+1, right, target);  // 在右半部分继续查找
    } else {
        return recursive_search(arr, left, mid-1, target);  // 在左半部分继续查找
    }
}
// 分治法实现元素查找算法
int divide_search(int arr[], int left, int right, int target)
{
    while (left <= right) {
        int mid = left + (right - left) / 2;  // 计算中间位置
        if (arr[mid] == target) {
            return mid;  // 查找成功，返回元素下标
        } else if (arr[mid] < target) {
            left = mid + 1;  // 在右半部分继续查找
        } else {
            right = mid - 1;  // 在左半部分继续查找
        }
    }
    return -1;  // 查找失败，返回-1
}
int main()
{
    int arr[NUM_COUNT];
    srand(time(NULL));  // 设置随机数种子
    printf("随机生成的数组为：");
    for (int i = 0; i < NUM_COUNT; i++) {
        arr[i] = rand() % MAX_NUM + 1;  // 随机生成1-100之间的整数
        printf("%d ", arr[i]);
    }
    printf("\n请输入要查找的元素：");
    int target;
    scanf("%d", &target);
    int index = recursive_search(arr, 0, NUM_COUNT-1, target);  // 递归查找
    // int index = divide_search(arr, 0, NUM_COUNT-1, target);  // 分治法查找
    if (index == -1) {
        printf("未找到该元素\n");
    } else {
        printf("该元素位于数组的第%d个位置\n", index+1);
    }
    return 0;
}