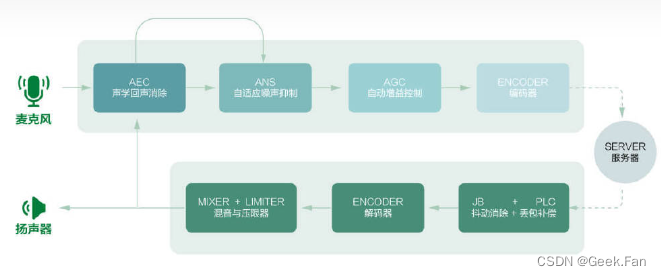
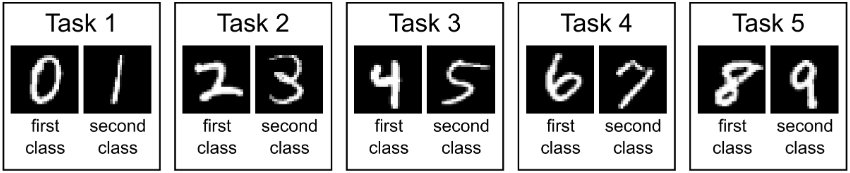
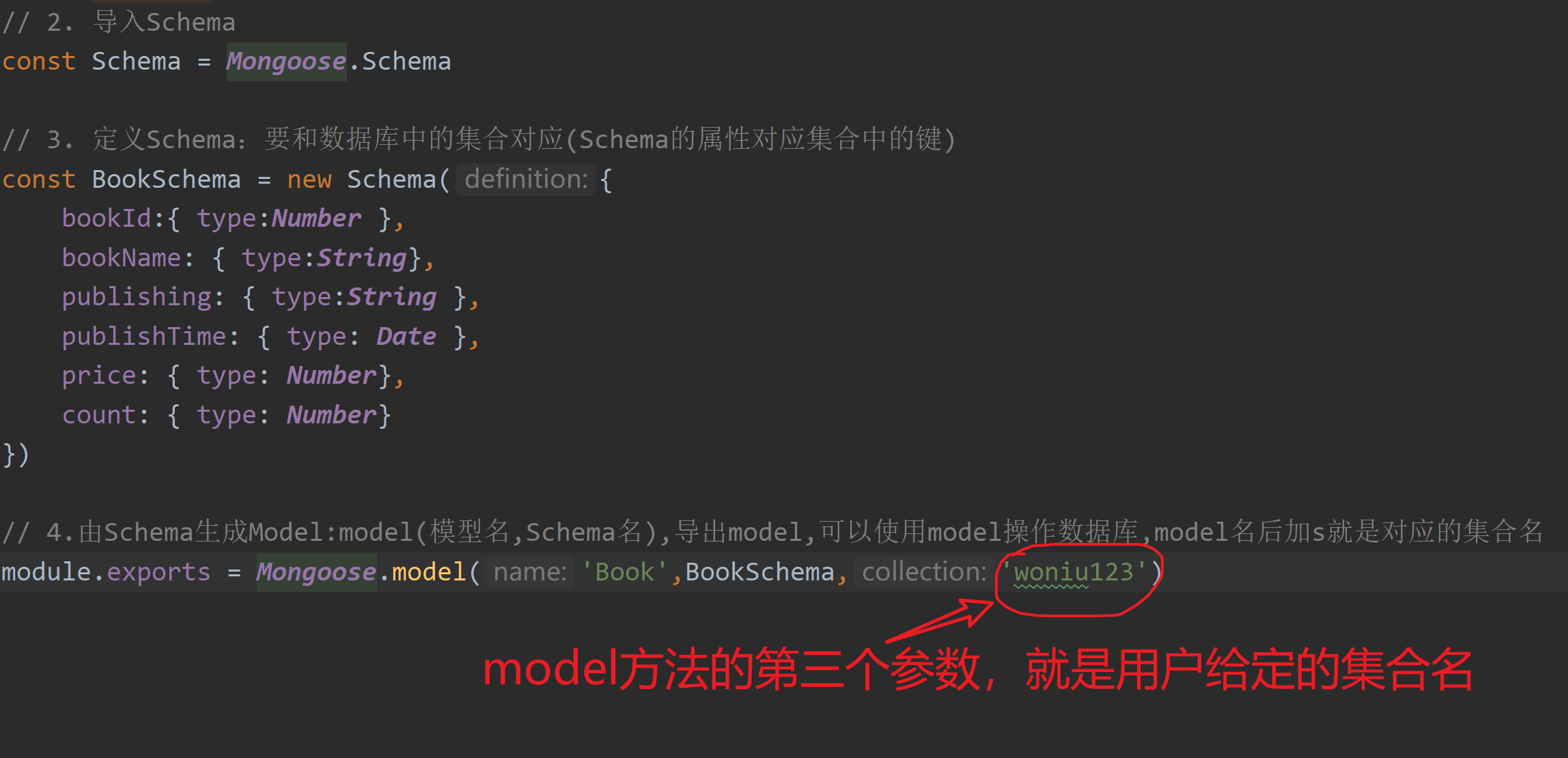
本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
我们知道,随机游走序列是到当前时间为止白噪声实现(white noise realization)的简单求和。换句话说,随机游走序列中的对下一个时间点值的估计(预测)是通过从高斯分布中抽样获得(或者说服从高斯分布)。还要注意,股票价格的对数通常被建模为随机游走。
现在假设有一个任务就是观察随机游走。观察的结果是得到一个随机游走序列。就股价而言,观察任务意味着得到股票价格的时间序列。我们周期性地观察股票的价格并记录它们。股票的价格时序形成了随机游走。
注意,我们观察到的股票价格都是准确无误的,因此能够无误地观察(observe)股价时序。问题是如果观测(observation)是没有错误的,那么卡尔曼滤波模型就不适用了。为什么我们还需要这样做(需要卡尔曼滤波)?
通常来说,任何时刻的股价都应该体现供需平衡的情况,这个价格叫做均衡价格(equilibrium price)。在这种情况下,周期性测量方法相当于使用特定时间的观测价格作为时间间隔的均衡价格。所以,在每个时间间隔结尾得到的观测价格相当于是对这个时间间隔均衡价格的求近似值(approximation)。那么,观测误差(observation error)就变得有意义了。因而,可以把卡尔曼滤波方法用在股价上,具体是用在股价求对数之后的序列即一个随机游走过程上。
现在从时间开始,观测到的状态(股价)是
,实际的状态(股价)是
。观测的式子表示为:
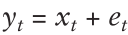
根据随机游走,我们有:
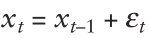
我们把这些写成一个序列:

用矩阵的方式表示:
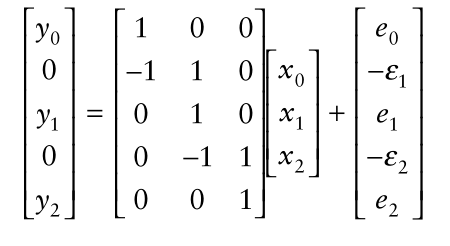
进一步表示成:
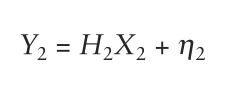
下标的2表示估计的状态的数目。我们有五个式子(方程),三个未知数,
,
。因为式子比未知数多,这种系统又叫做超定集(overdertermined set)。如果每个阶段的误差都是来自相同的,独立的正态分布,对于超定集的解可以用最小二乘法获得:
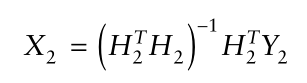
去到下一个观测值,我们有以下的矩阵,我们对状态的估计就是这个矩阵的解:
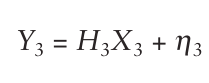
这个系统就有七个式子(方程),四个未知数。同样我们解这些方程,就得到的估计。但是,随着观测值的增加,矩阵增大,计算的花费也增大。而卡尔曼滤波方法就是救星。因为在卡尔曼滤波中,前一步的结果用于下一步状态的预测,比如前一步计算好的
及它的方差,可以用于
的预测。这样,评估下一步的计算成本是相同的,无论我们计算多少的时间步长。
不管怎样,卡尔曼滤波情况下状态估计的最终结果与使用最小二乘法求解方程组的结果相同。注意,我们在这个过程中做出了一个重要的假设,即每个时间步长的状态方差等于观测方差。(还有一个假设是误差分布独立性。)因此,根据前面的假设,卡尔曼滤波器归根结底是方程的最小二乘解。不同的是卡尔曼滤波中解是以递归方式计算的。因此,卡尔曼滤波器被称为递归最小二乘法。
相同和独立误差分布(误差是独立同分布的)的假设体现在误差的协方差矩阵中。独立性也意味着误差不相关。因此,协方差矩阵中的非对角元素均为零。协方差矩阵中的对角元素是误差项的方差。如果它们来自相同的分布,那么方差应该是相同的。因此,在这种情况下,协方差矩阵可以表示为单位矩阵乘以常数。
现在我们回到刚才的方程组的解的讨论中。结果表明,该组方程在给定时间的估计状态可以表示为观测值的加权线性组合。此外,权重实际上是斐波那契数的比率。一个斐波那契数列是犹如以下的数列:
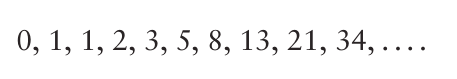
即前两项之和等于第三项:
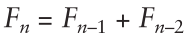
对于状态的估计可以表示为:
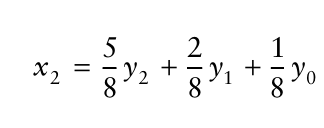
类似地,的估计表示为:
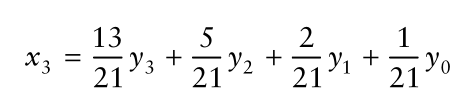
一般来说,我们有:
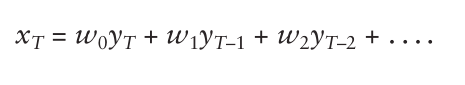
且,
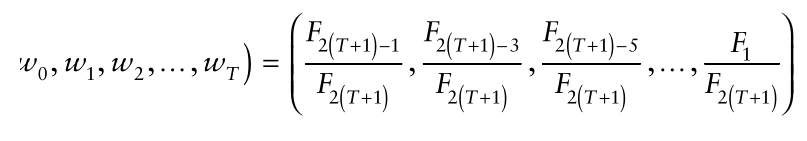
注意,以上权重公式成立的前提假设是状态的方差与观测的方差是相同的。也就是说,如果我们要用以上的公式,那么每一步我们都要估计状态的方差和观测的方差。
在随机游走中,状态方差可以被估计为innovation的方差。将股票价格序列建模为随机游走,innovation对应于股价序列的周期收益。因此,这种情况下的状态方差就是周期回报的方差。这种计算在金融界相当普遍,通常被称为历史波动率(historical volatility)。然而,观测方差的估计有点不一样。在一个时间段内我们除了观察收盘价,我们还观察了该时间段内股价最高价和最低价。观测误差的方差是该时间段内股价的波动性。这种波动性被最高价和最低价所描述。存在几种基于高-低价格估算波动率的方法,可以使用任何一种方法来估计观测方差。一旦状态和观测方差已知,我们就可以应用卡尔曼滤波方法了。