文章目录
- 前缀和
- 差分
- 大整数加减乘除
前缀和
前缀和，即preSum[i] = nums[i-1] +nums[i-2] + ··· + nums[0]。一般地，我们会让preSum[0] = 0。
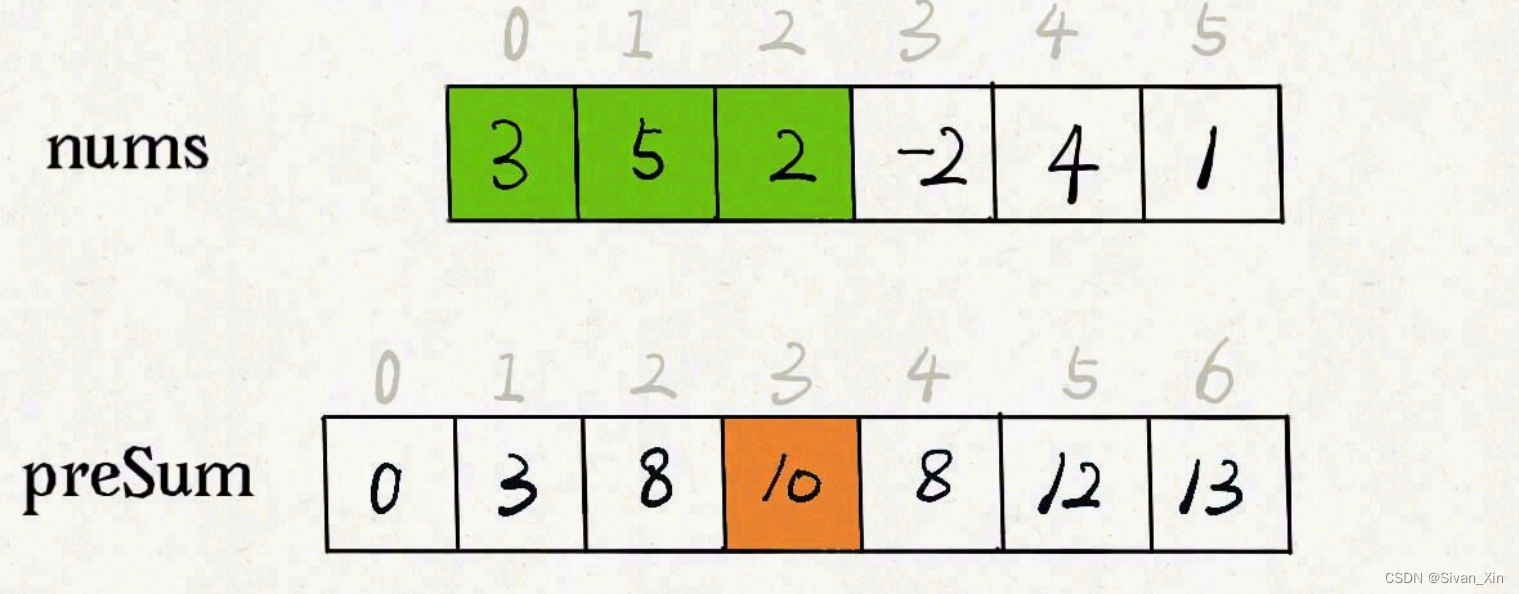图：preSum[3] = nums[2] + nums[1] + nums[0]。
构造前缀和数组对我们来说是简单的，只需要会用以下代码：
int [] nums = {3,5,2,-2,4,1};
//构建前缀和数组。
preSum = new int [nums.length+1];
//preSum[0]默认为0，从1开始放入前缀和。
for(int i=1;i<preSum.length;i++){
preSum[i]=preSum[i-1]+nums[i-1];
}
}
使用前缀和主要用来解决区域和的问题，如果想求出数组内left到right的和。就可以使用前缀和数组。
public int sumRange(int left, int right) {
return preSum[right+1] - preSum[left];
}
-
二维数组的前缀和
我们需要定义一个前缀和数组
preSum [i][j]记录 matrix 中子矩阵 [0, 0, i - 1 , j - 1] 的元素和。同一维前缀和一样，一般我们会让preSum[0~i][0] = 0/preSum[0][0~j] = 0。构造二维前缀和的模板如下：
//构建二维前缀和 private int [][]preSum; public NumMatrix(int[][] matrix) { int m=matrix.length; int n=matrix[0].length; preSum = new int [m+1] [n+1]; for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ preSum [i][j] = preSum[i][j - 1] + preSum[i - 1][j] -preSum[i-1][j-1] + matrix[i-1][j-1]; } } }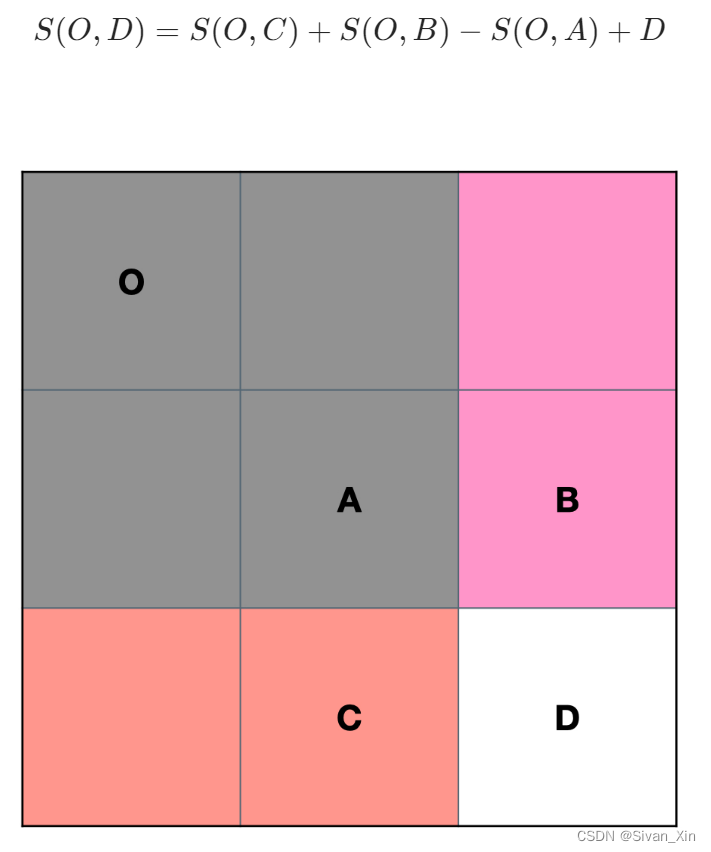
图：构造二维前缀和
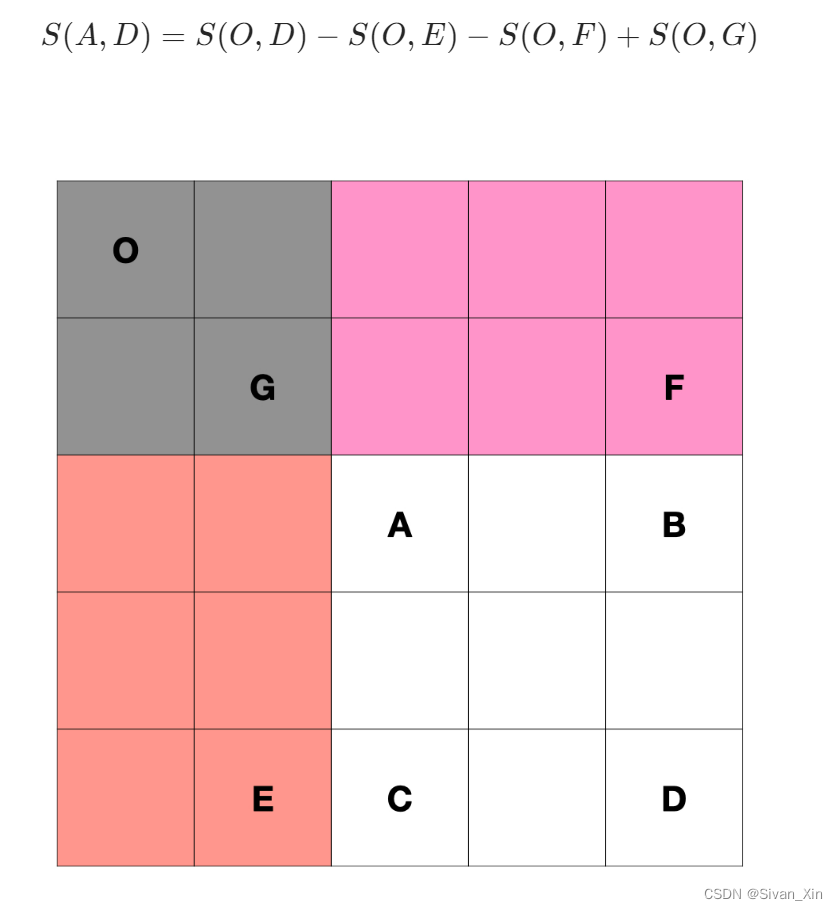
当然，如果想要求出matrix矩阵[row1,col1,row2,col2]区间的和，使用如下模板：
public int sumRegion(int row1, int col1, int row2, int col2) {
return preSum[row2+1][col2+1]
-preSum[row2+1][col1] - preSum[row1][col2+1]
+ preSum[row1][col1];
}
差分
差分数组，即遵循diff[i]=nums[i]-nums[i-1]的一个数组。
如果修改原数组left到right的值，不需要遍历，只是将 diff[left]+=data 且 diff[rght+1]-=data即可。
如果要将差分数组转换成原数组，则需要nums[i]=nums[i-1]+diff[i]，也就是前缀和的做法。即前缀和与差分是互逆的。
public class Demo {
private static final int [] nums = {1,2,6,7,9};
//原数组构造差分数组
public static int[] getDiff(int []nums){
int [] diff = new int[nums.length];
diff[0]=nums[0];
//原数组—差分求法—差分数组
for(int i=1;i<nums.length;i++){
diff[i]=nums[i]-nums[i-1];
}
return diff;
}
//更改原数组的值（left到right）
public static void increase(int left,int right,int []diff,int num){
diff[left]+=num;
if(right<diff.length - 1){
diff[right+1]-=num;
}
}
//差分数组构造原数组
public static int [] getNums(int []diff){
int nums1[]=new int [nums.length];
nums1[0]=diff[0];
//差分—前缀和求法—原数组
for(int i=1;i< nums1.length;i++){
nums1[i]=nums1[i-1]+diff[i];
}
return nums1;
}
}
-
二维差分数组
关于二维差分数组的构建：
我们可以先假想nums原数组为空，那么diff数组一开始也为空，但是实际上nums数组并不为空。因此我们每次让diff以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 nums[i] [j]，等价于原数组nums中(i,j) 到(i,j)范围内 加上了nums[i][j] ,因此执行n*m次插入操作，就成功构建了差分diff数组。如果要修改原数组[x1,y1,x2,y2]范围的值，只需要修改diff数组的四个位置，也就是insert函数。
import java.util.Scanner; public class T798 { static int n = 1001; static int m = 1001; static int N = 1001; static int data; static int [] [] diff = new int [N][N]; static int [] [] nums = new int [N][N]; static int [] [] ans = new int [N][N]; //插入函数 static void insert(int x1,int y1,int x2,int y2,int c) { diff[x1][y1] += c; diff[x2 + 1][y1] -= c; diff[x1][y2 + 1] -= c; diff[x2 + 1][y2 + 1] += c; } public static void main(String[] args) { Scanner s = new Scanner (System.in); m = s.nextInt(); n = s.nextInt(); data = s.nextInt(); for(int i = 1;i<=m;i++) { for(int j = 1;j <= n;j++) { nums[i][j] = s.nextInt(); } } //构建二维差分数组。 for(int i = 1;i<= m;i++) { for(int j = 1;j<= n;j++) { insert(i,j,i,j,nums[i][j]); } } while( data-- != 0) { int row1 = s.nextInt() ; int col1 = s.nextInt() ; int row2 = s.nextInt() ; int col2 = s.nextInt() ; int add = s.nextInt(); insert(row1,col1,row2,col2,add); } //二维差分转为原数组——就是求差分数组的前缀和。 for(int i = 1;i<=m;i++) { for(int j = 1;j<=n;j++) { ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1] + diff[i][j]; System.out.print(ans[i][j] +" "); } System.out.println(); } } }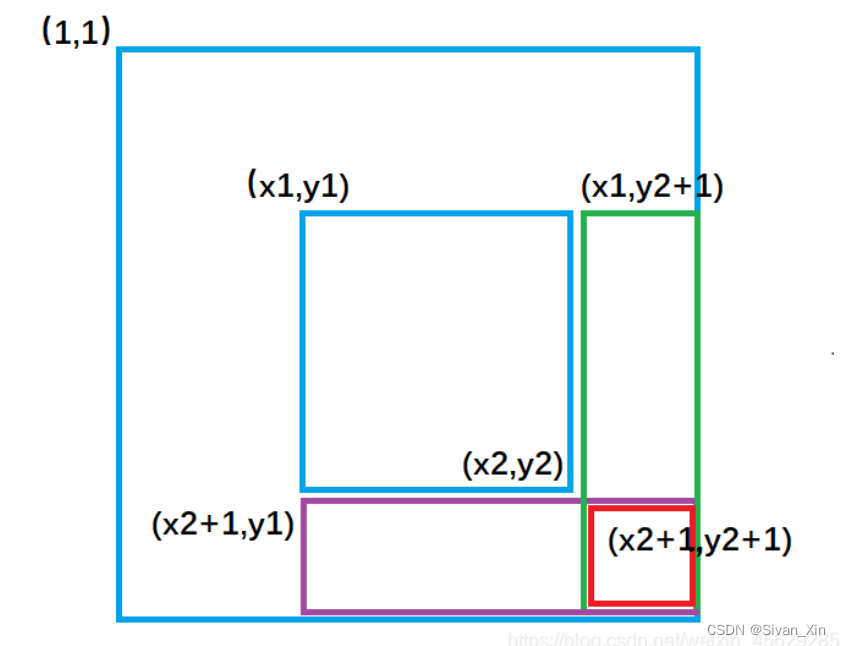
图：修改二维差分数组的值，对原数组的影响。
大整数加减乘除
在Java中有两个类BigInteger和BigDecimal分别表示大整数类和大浮点数类
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner (System.in);
BigInteger n1 = s.nextBigInteger();
BigInteger n2 = s.nextBigInteger();
//加法
System.out.println(n1.add(n2));
//减法
System.out.println(n1.subtract(n2));
//乘法
System.out.println(n1.multiply(n2));
//除法
System.out.println(n1.divide(n2));
}
}
