文章目录
- 前言
- 0、题目
- 一、暴力查找
- 二、二分查找
- 三、有序二叉树
- 总结(代写匿名信)
前言
很明显小艺的口红问题是考的是查找算法,对于这种一次性查找,直接暴力就行了,当然咱是为了学习,所以用来练练各种查找,基础是二分查找法!其它方法大多基于二分查找改进的。更高级的二叉排序树查找,B树、B+树啥的,也统统都得排序。这里用暴力法、二分法、二叉排序树这三种有代表性的方法来解。嗯~ 这个题目测试数据应该有问题,反正我0分~ 好像所有我做不出100分的,我都说是题目问题哈
提示:以下是本篇文章正文内容,下面案例可供参考
0、题目
题目描述:
小艺的口红越来越多了。 小艺想从自己的口红堆里挑选一个色度大于等于x的最小口红的色度。 小艺每天都会为了这个问题发愁。 作为小艺的忠实狗腿子,小Q决定帮小艺编一个程序,录入所有的口红色度。 然后智能的选择最小色度。
输入描述:
第一行输入整数n,q。(1<=n,q<=1e5)表示口红的数量和询问次数。 第二行输入n个整数表示小艺口红的颜色t。(1<=t<=1e9) 以下 q-1 行每行输入一个整数h。(1<=h<=1e9)表示询问色度。
输出描述:
每个询问对应一个输出占一行。
示例的数据是这样的vector = [[1, 5, 9, 10, 2], [6], [7]]
一、暴力查找
从示例看,暴力法是好使的。
class Solution:
def __init__(self) -> None:
pass
def solution(self, n, q, vector):
result = []
# TODO: 请在此编写代码
for i in range(1, q):
max = int(1e9)
for v in vector[0]:
if vector[i][0] <= v <= max:
max = v
result.append(str(max))
return result
这写法看上去还是比较科学的,不断减小max的值。一直到max值不能再小了就是它了。只需遍历一次、逻辑简单、运行速度快!
二、二分查找
class Solution:
def __init__(self) -> None:
pass
def solution(self, n, q, vector):
result = []
# TODO: 请在此编写代码
vector[0].sort()
for i in range(1,q):
l, r = 0, n
for v in vector[0][l:r]:
mid = (l+r)//2
if vector[i][0] > vector[0][mid] and vector[i][0] <= vector[0][mid+1]:
result.append(str(vector[0][mid+1]))
break
elif vector[i][0] > vector[0][mid]:
l, r = mid+1, n
else:
l, r = l, mid-1
return result

从示例来看它也是好使的,如果要查找的值多了,这个方法会比暴力法快很多,二分查找的逻辑也简单,先对vector[0].sort()排序,然后不断的把列表分成左右两份。类似于猜数字游戏:我手上有纸条写了一个整数,并告诉你它在1-100之间,请你来玩猜数字游戏,我只会告诉你猜的数是大了还是小了,聪明的你肯定先猜50,如果大了就再猜25…以此类推,二分查找法就是根据这个游戏来的。结合代码一看就明白了吧~
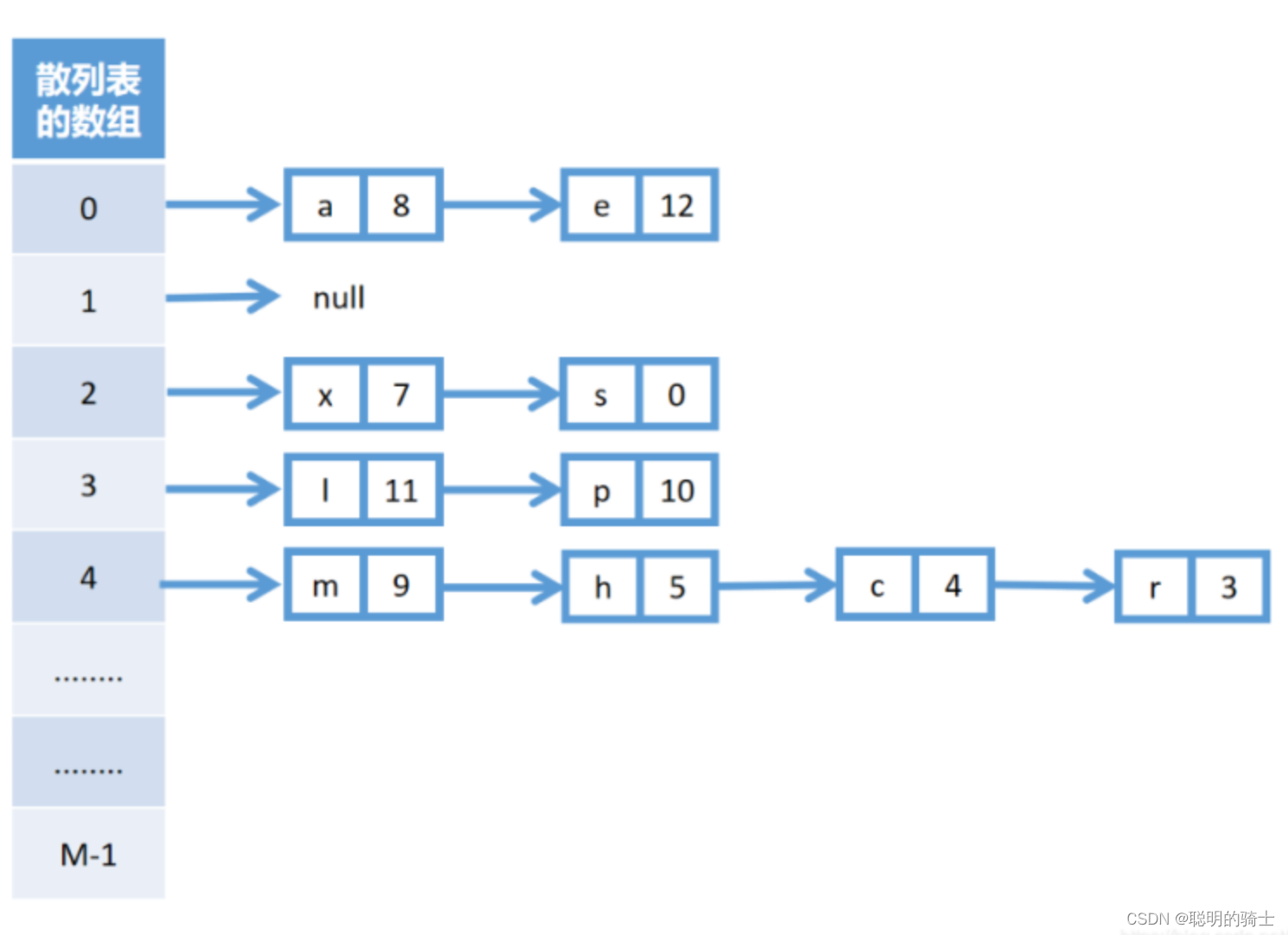
三、有序二叉树
# 定义一个二叉树节点类结构体
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Solution: # 定义一个有序二叉树类
def __init__(self, v):
self.root = None
vec = v[0]
for x in vec:
self.insert(x)
def insert(self, val): # 插入节点
if not self.root:
self.root = TreeNode(val)
return
curr = self.root
while curr:
if val < curr.val:
if not curr.left:
curr.left = TreeNode(val)
return
else:
curr = curr.left
else:
if not curr.right:
curr.right = TreeNode(val)
return
else:
curr = curr.right
def solution(self, target, curr=None, res=1e9): # 按题意搜索
if not curr:
curr = self.root
while True:
if target <= curr.val <= res:
res = curr.val
if curr.left and target < curr.val:
curr = curr.left
self.solution(target, curr)
elif curr.right and curr.val < target:
curr = curr.right
self.solution(target, curr)
else:
break
return res
if __name__ == "__main__":
from random import randint
arr_temp = [] # [int(item) for item in input().strip().split()]
n = randint(5, 20) # int(arr_temp[0])
for i in range(n):
arr_temp.append(randint(1, 99))
q = randint(2, 5) # (arr_temp[1])
vector = list()
vector.append(arr_temp)
for i in range(q-1):
vector.append([randint(1, 99)])
print(vector)
sol = Solution(vector)
for x in vector[1:]:
result = sol.solution(x[0])
print('result =', result, end=", ")
这个解法就属于高级货了,图论算法都算是高级算法了。当然二叉树还是相对比较简单的。这个算法的中心思想是:先定义一个根节点,比根节点小的放到左边去,比根节点大的放右边去,再来一个比根节点大的,我就去右边再根据大小找个地方放。就像树一样,不停的长出分枝,所以叫有序二叉树。代码中的insert函数就是用来生成树的。
代码中的TreeNode这个单独的类,是用来存放数据结构的。python没有struck,就用类来做数据结构了,C/C++中一般会用struck来这么定义,从一个单独的节点来看,这个类定义了根的值val,并记录了它的左右两边的节点。
代码中的solution函数是用来按题意搜索的,这题的搜索比较麻烦,是要找到一个从左边最接近的值,这里定义了一个curr用来表示当前节点,默认是None,下面只要按照大小从左或右边不停递归就行了。
笔者都用上这高级算法了可还是0分!很显然是题目错了,所以笔者自己写了一个随机数测试的办法(就是if __name__ == "__main__":)下面的部分,是从原代码那改来的:
[[95, 14, 1, 73, 60, 28, 35, 85, 22, 15], [20], [1], [36]] result = 22, result = 1, result = 60,
这里只给出一次测试结果来证明一下这个程序是可靠的,事实上我测了很多次,毕竟写一次有序二叉树也不容易,这种东西在实际工作中,几乎没有可能用到,因为大多数语言都有现成的方法函数来解决此类查找问题,谁吃饱了撑得慌去写这个,再说就算自己写了吧,还多半不如编程语言自带的函数来得效率高…有兴趣的看官可以自己试试。
总结(代写匿名信)
今天的另两题,近视的小张题目描述太长,对笔者的阅读理解能力是个特大考验,还是先去小学回炉语文再来吧~
另一个“代写匿名信”倒是简单,顺手也给出解法:
def solution(self, words, msg):
result = None
# TODO: 请在此编写代码
for m in msg:
if m != " ":
i = words.find(m)
if i == -1:
result = "No"
break
else:
words = words[:i] + words[i+1:]
result = "Yes"
return result
就几行代码搞定,以上代码的逻辑是:去words中查找每个msg中的字符,嗯~除了空格以外,因为空格是不用字符的。不注意这点只能过90%,别问我怎么知道的… 在words中找到后就把它删了,循环完自然就知道能不能写成信了。
还想到个办法:用try和except,因为字符串的index方法找不到就会报错,报错自然会被except捕捉到,就可以NO了,try成功就删除index方法找到的值,也是循环一次就搞定。逻辑差不多的,有兴趣的可以写着试试。