数据分析示例-python

今天呢，博主把之前做过的一个小课题拿出来展示一下，当然这个课题呢做的工作量很大，也用到了很多可以参考的技术和代码，做数据分析工作的可以尝试学习学习。
这篇博客，我们先从数据集开始介绍。
对了数据集，我会上传到，我的资源，如果下载不了的可以私聊我。
数据集是两个csv文件，一个是data.csv,一个是predict.csv，第一个文件data.csv包含了三个抖音直播间的相关数据
列如：‘索引’,“自然流量详情”,“付费流量详情”,“UV价值”,“新增评论数”,“时间”,“新增粉丝数”,“离开人数”,“新加团人数”,“成交金额”,“在线人数”,
“进入人数”,“成交订单数”,“成交人数”,“企业唯一标识”。
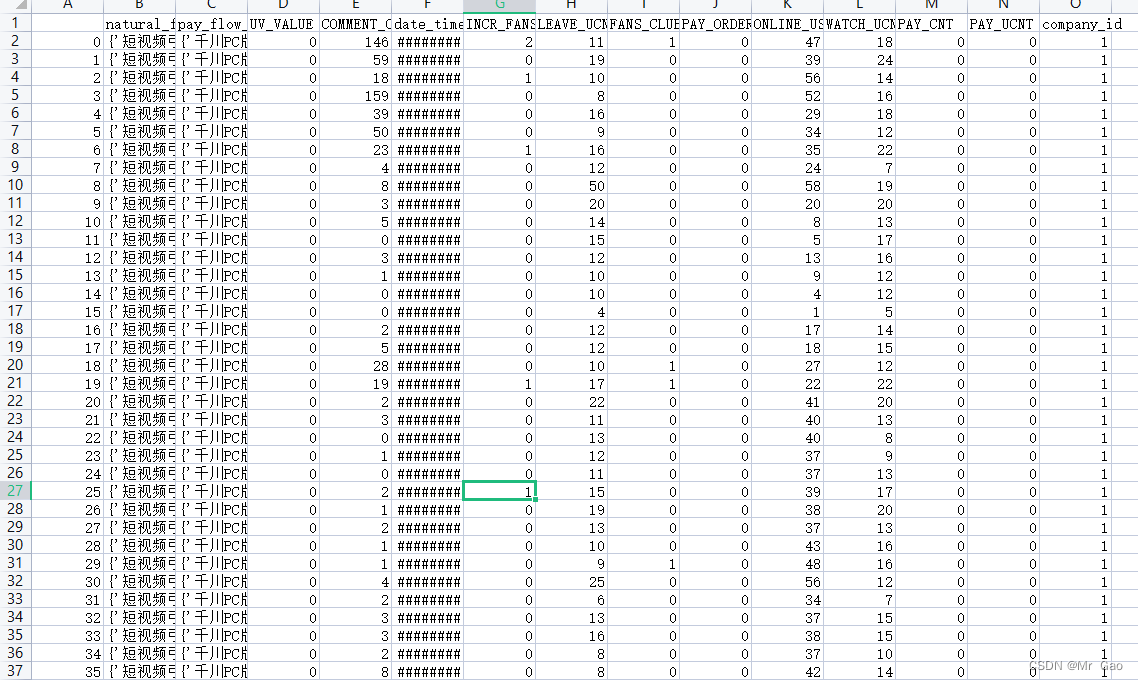这个从英文名就可以猜到每一列的一个信息。
对于predict.csv这个文件，这个文件呢，比data.csv少了一个企业标识符：
‘索引’,“自然流量详情”,“付费流量详情”,“UV价值”,“新增评论数”,“时间”,“新增粉丝数”,“离开人数”,“新加团人数”,“成交金额”,“在线人数”,
“进入人数”,“成交订单数”,“成交人数”，说明predict是一个直播间的数据。

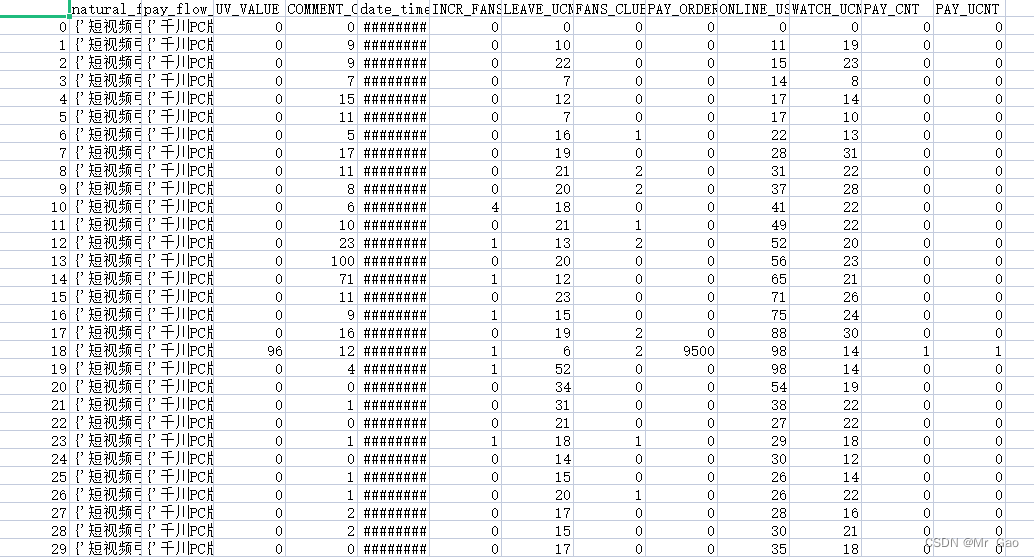
下面我们数据中的信息：
首先我们能需要先读取数据：

#导入数据，编码方式为utf-8，每个字段的分割符为一个tab
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import os
import time
import statsmodels.api as sm
from scipy import stats
from statsmodels.tsa.arima.model import ARIMA
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题




name_data=['索引',"自然流量详情","付费流量详情","UV价值","新增评论数","时间","新增粉丝数","离开人数","新加团人数","成交金额","在线人数",
"进入人数","成交订单数","成交人数","企业唯一标识"]
name_predict=['索引',"自然流量详情","付费流量详情","UV价值","新增评论数","时间","新增粉丝数","离开人数","新加团人数","成交金额","在线人数",
"进入人数","成交订单数","成交人数"]
data=pd.read_csv(r"C:\Users\gaoxi\Desktop\data\data\data.csv",encoding="utf-8",names=name_data)
predict=pd.read_csv(r"C:\Users\gaoxi\Desktop\data\data\predict.csv",encoding="utf-8",names=name_predict)

之后我们可以查看数据集的相关基本信息：

#查看数据集的基本信息

print(data.columns)
print(data.info())
print(predict.info())

print(data.head())
print(predict.head())

下面我们对数据进行处理，因为数据的质量比较高，所以数据处理部分的工作比较少，代码如下：

#数据类型转化
column_data=data.columns.tolist()
remove=['索引',"自然流量详情","付费流量详情","时间"]

for i in remove:
        column_data.remove(i)
for i in column_data:
        data[i]=data[i].astype('float')
column_pre=predict.columns.tolist()

for i in remove:
        column_pre.remove(i)
for i in column_pre:
        predict[i]=predict[i].astype('float')
#时间格式类型转化      
data["时间"] = pd.to_datetime(data["时间"])

predict["时间"] = pd.to_datetime(predict["时间"])
#缺失值处理
print(data.info())
print(predict.info())
data=data.dropna()
print(data.info())

#print(data["时间"])
#因为只有data有缺失值，而且只有几条，所以我们可以进行直接删除，不影响后续数据分析
#异常值处理

好的，之后，我们即可进行相关信息挖掘：

下面是特征箱型图的绘制代码：

def plot1():
   
   
    #异常值是指远远偏离整个样本总体的观测值；异常值我们通常采用箱线图来处理，处在上下限之外的数据都都属于异常值
    for j in range(1,4):
        plt.figure(figsize=(80,60))
       
  
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(4,4,i+1)#将画布分割为6行8列
            sns.boxplot(data[data['企业唯一标识']==j][column_data[i]],orient="v",width=0.5)#每一个小区域画出箱型图
        #    plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel
    
    
        plt.show()

    plt.figure(figsize=(80,60))
   
 

    for i in range(len(column_pre)):
        plt.subplot(4,4,i+1)#将画布分割为6行8列
        sns.boxplot(predict[column_pre[i]],orient="v",width=0.5)#每一个小区域画出箱型图
       # plt.xlabel(column_pre[i],fontsize=12)#x轴的注释为xlabel
    
    plt.show()

    #经过箱型图分析，我们发现直播间各种流量箱型图都极为不稳定。所以可能，本身就不存在异常值，跟这个直播的性质有关，可能那天有个
    #比较著名的人突然来直播间就会带动各种流量，所以我们要特殊问题特殊分析，不需要进行异常值删除
plot1()

结果如下：



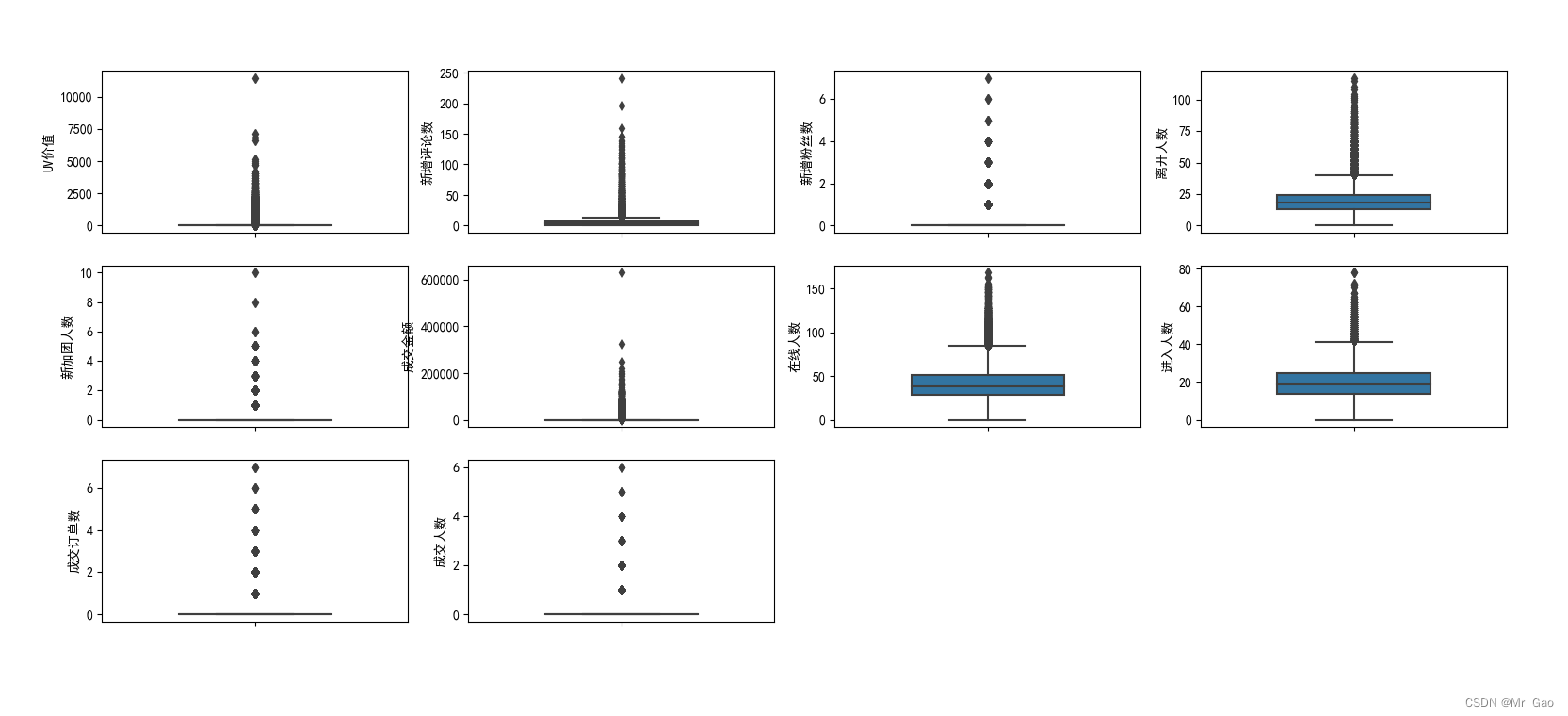
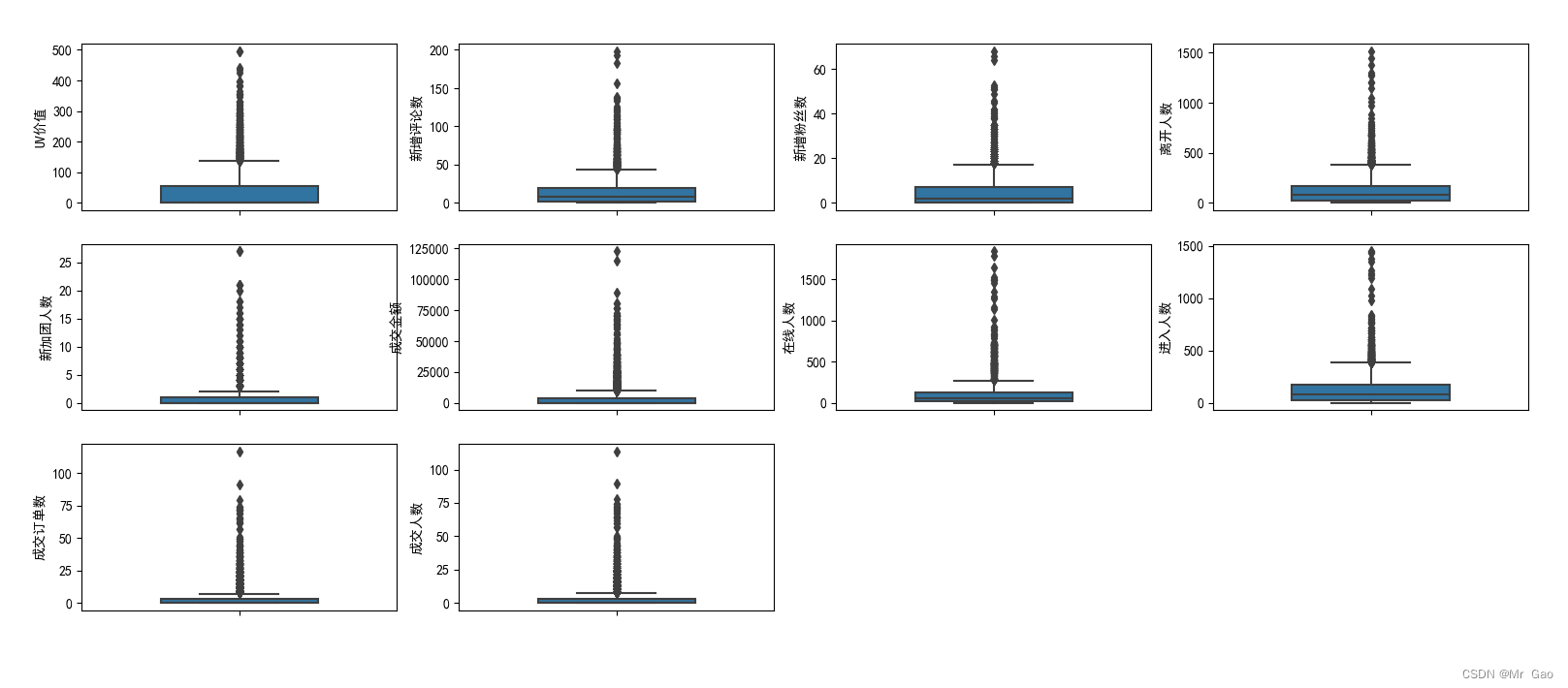
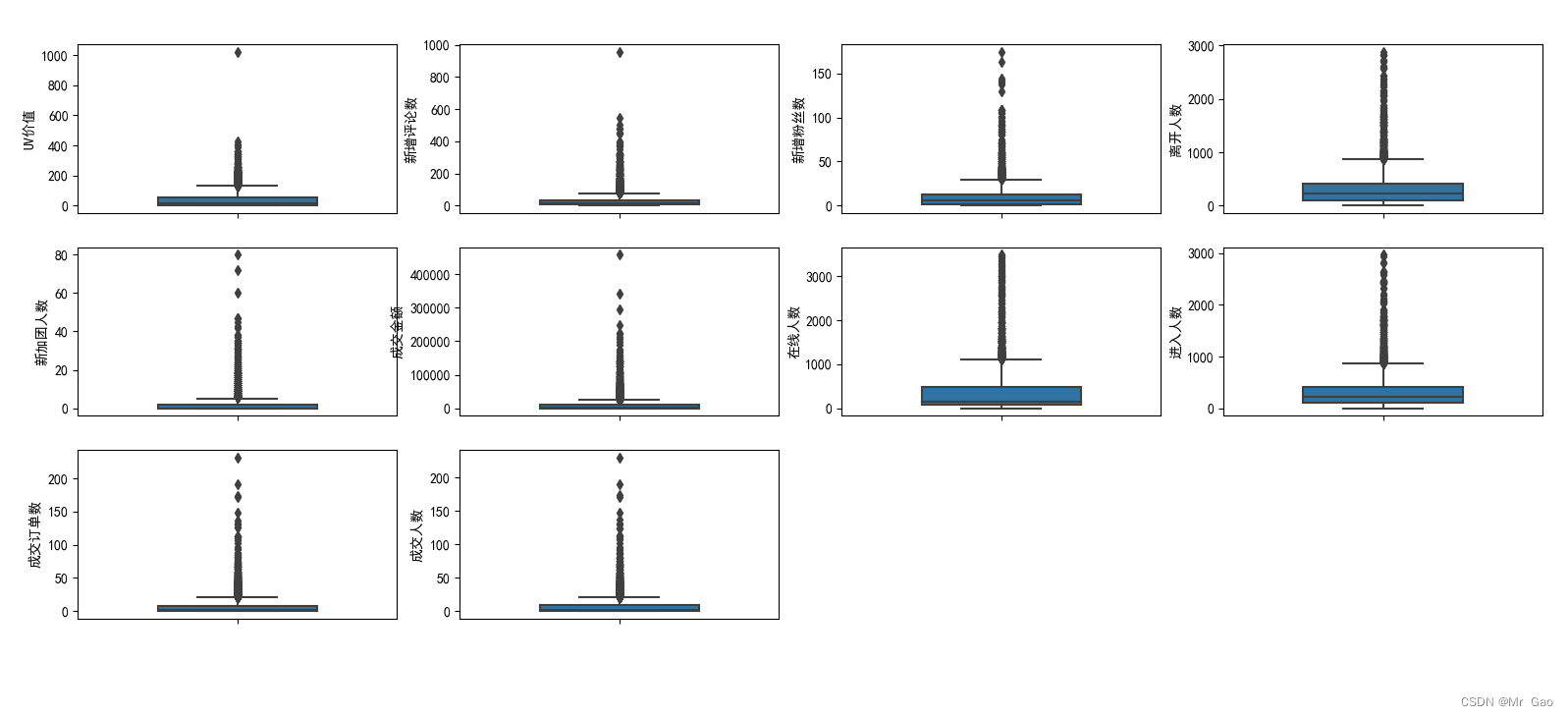
可从箱型图中提取相关价值，这里博主就不说了，只是给与大家代码参考。

下面是QQ图绘制，使得我们更好的了了解数据的分布：

#数据分布分析
#直方图和QQ图
#QQ图是指数据的分位数和正态分布的分位数对比参照的图，如果数据符合正态分布，所有的点都会落在直线上。
#我们首先绘制V0变量的统计分布
def plot2():
    for j in range(1,4):
        plt.figure(figsize=(80,60))
        p=1
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(6,4,p)#将画布分割为6行8列
            p=p+1
   
            stats.probplot(data[data['企业唯一标识']==j][column_data[i]],plot=plt)
            plt.xlabel(' ')#x轴的注释为xlabel
            plt.title(" ")#x轴的注释为xlabel
            plt.subplot(6,4,p)
            p=p+1
            df=data[data['企业唯一标识']==j][column_data[i]]
            print(df)
            sns.distplot(df,fit=stats.norm)#fit=stats.norm代表标准正态分布
    
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

        plt.show()
    plt.figure(figsize=(80,60))
    p=1
    for i in range(len(column_pre)):
            plt.subplot(6,4,p)#将画布分割为6行8列
            p=p+1
    
   
            stats.probplot(predict[column_pre[i]],plot=plt)
            plt.xlabel(' ')#x轴的注释为xlabel
            plt.title(" ")#x轴的注释为xlabel
            plt.subplot(6,4,p)
            p=p+1
            sns.distplot(predict[column_pre[i]],fit=stats.norm)#fit=stats.norm代表标准正态分布
    
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

    plt.show()
plot2()

绘图结果如下：

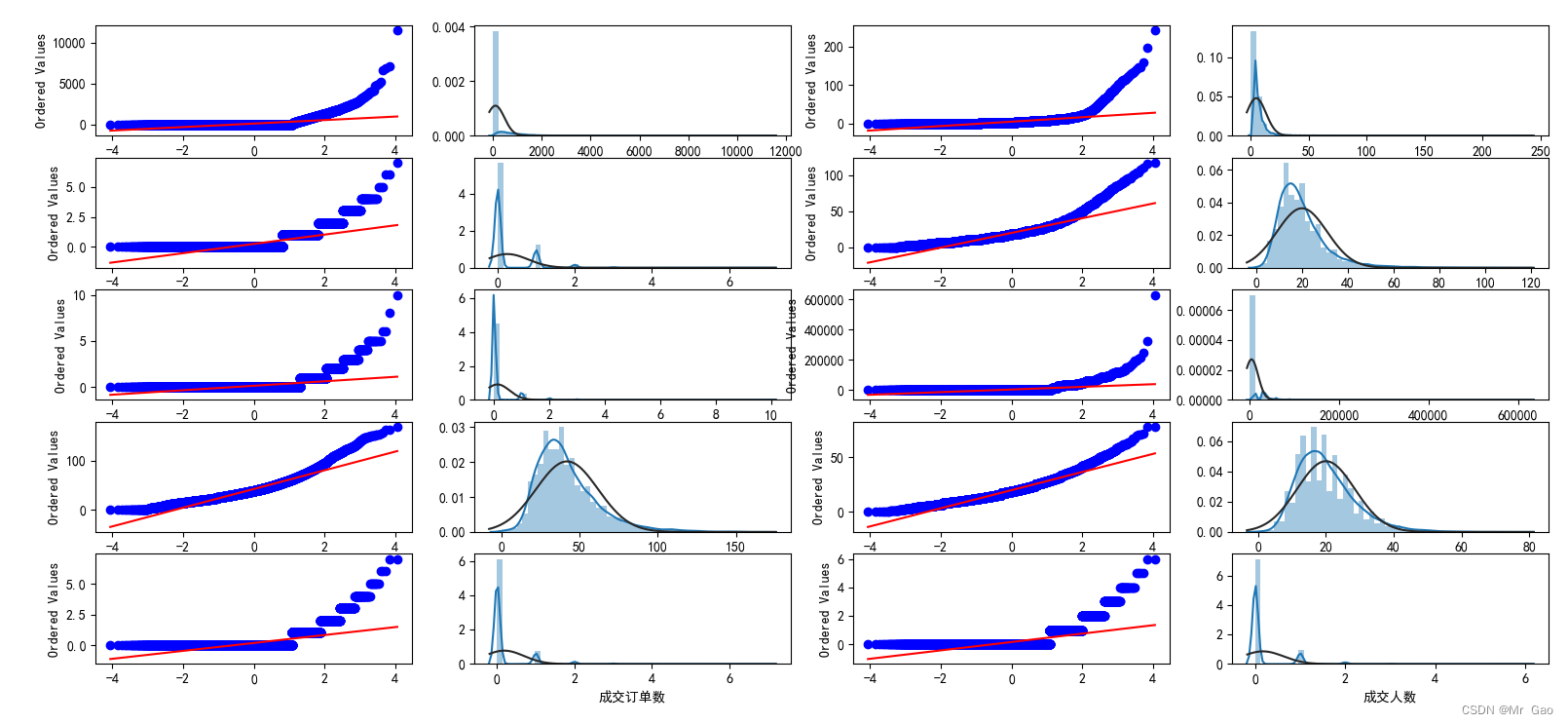
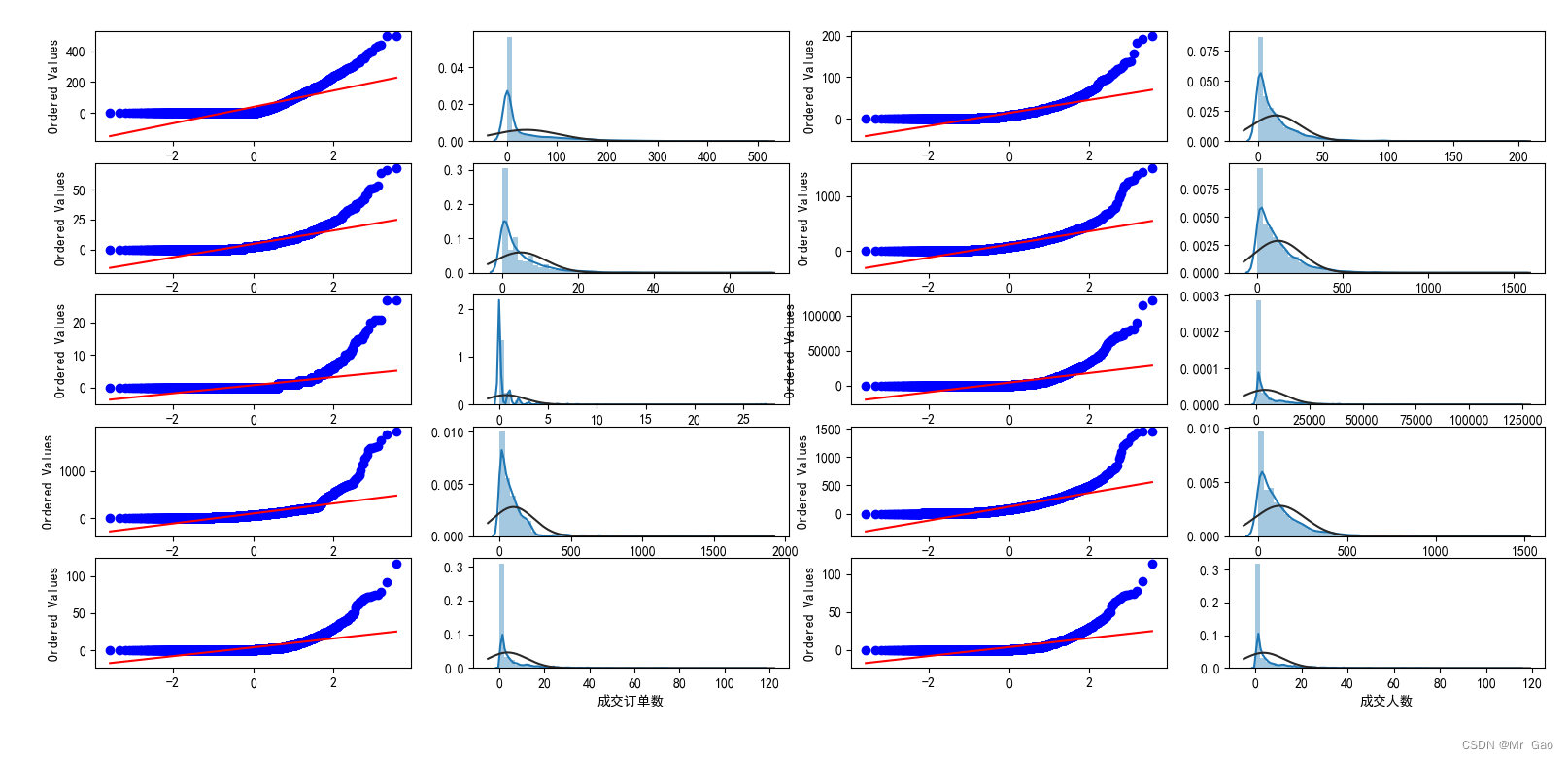
为什么会有多个图呢，因为不同的企业，我们要分开处理。

下面我们绘制不同企业数据的走势图：

def plot3():
   
    for j in range(1,4):
        plt.figure(figsize=(80,60))
        plt.title("X轴为时间 Y轴为流量")
        p=1
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(3,4,p)#将画布分割为6行8列
            p=p+1
   
            plt.plot(data[data['企业唯一标识']==j]['时间'],data[data['企业唯一标识']==j][column_data[i]])
            plt.xlabel(' ',fontsize=5)#x轴的注释为xlabel
            plt.xticks(rotation=30)
      #      plt.title(column_data[i])#x轴的注释为xlabel
         
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

      #  plt.show()
  
    plt.figure(figsize=(80,60))
    p=1
    for i in range(len(column_pre)):
        plt.subplot(3,4,p)#将画布分割为6行8列
        p=p+1
    
        plt.plot(predict['时间'],predict[column_pre[i]])
        #stats.probplot(predict[column_pre[i]],plot=plt)
        plt.xlabel(' ')#x轴的注释为xlabel
        plt.xticks(rotation=30)
        plt.title(" ")#x轴的注释为xlabel
       # plt.subplot(6,4,p)
        #p=p+1
        #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

    plt.show()


plot3()

绘图结果如下：

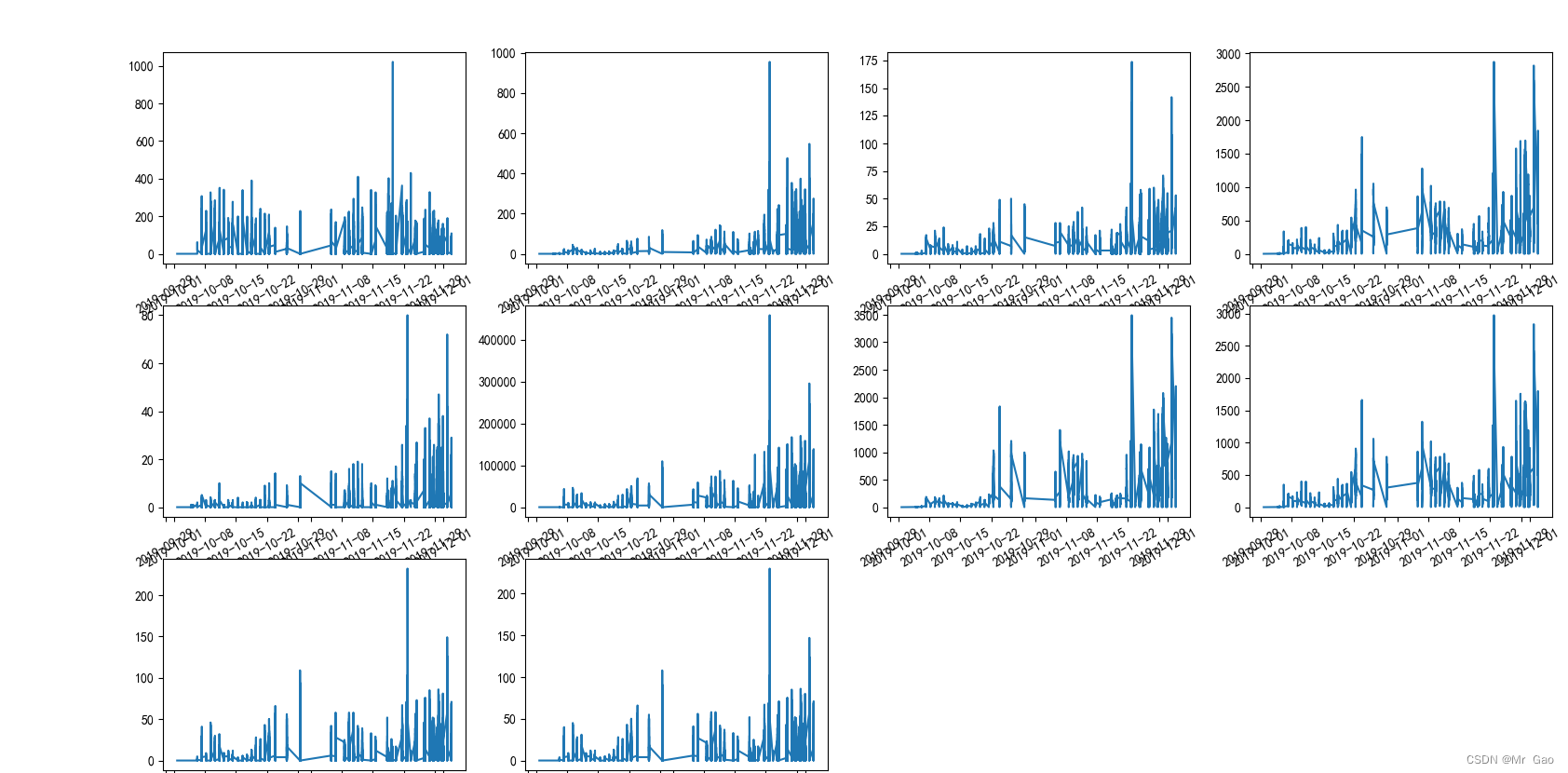
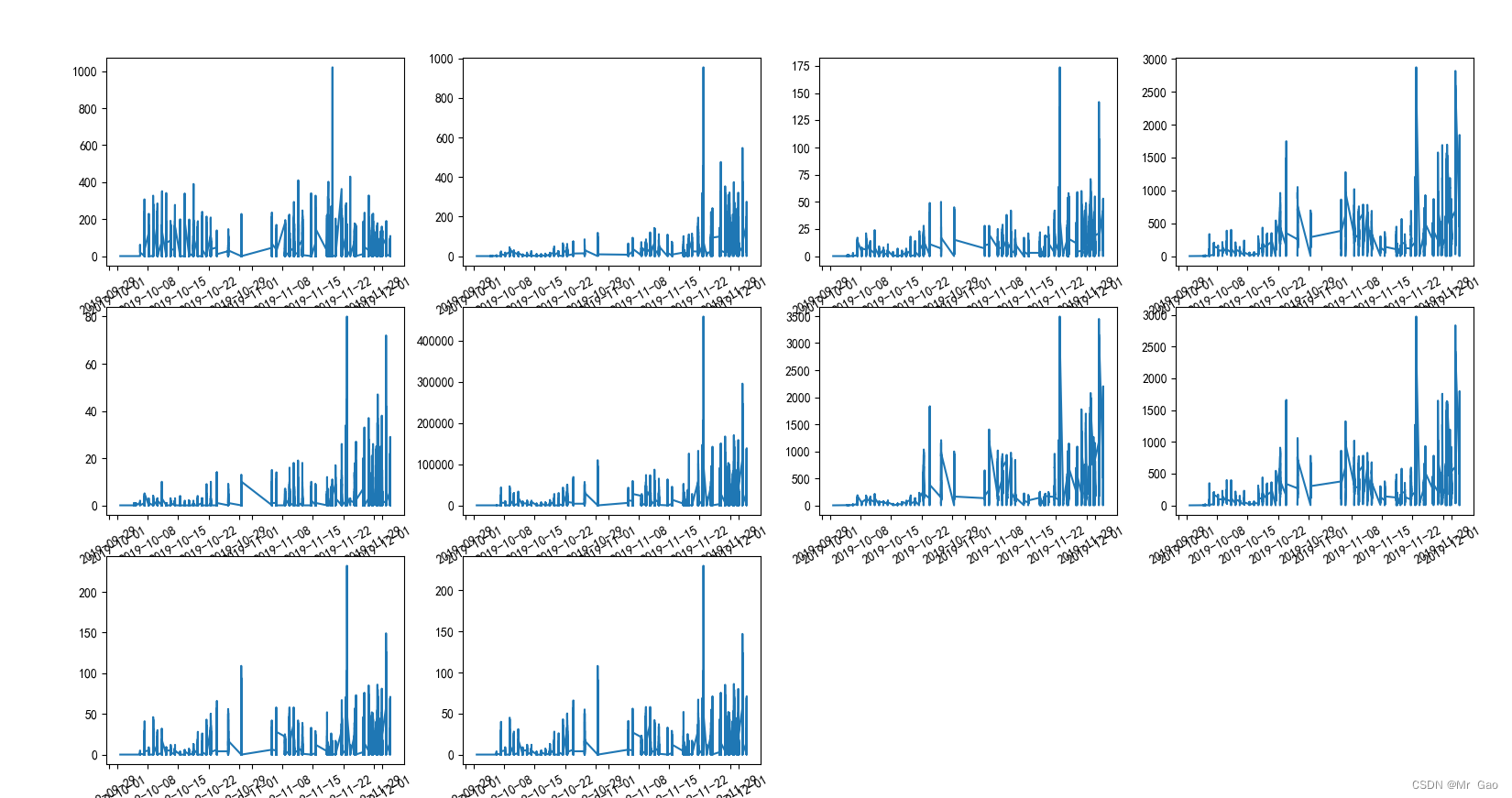
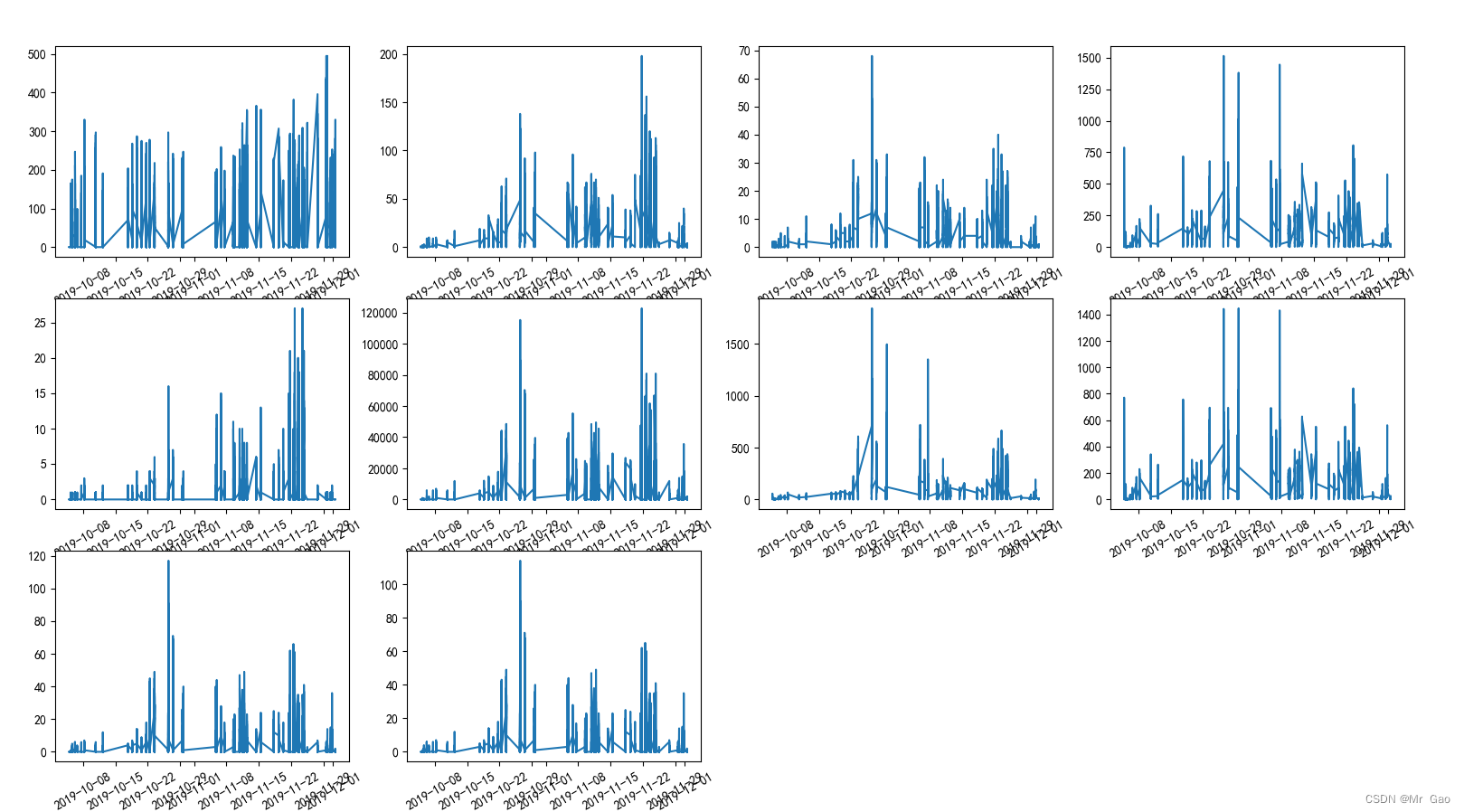
现在，我们绘制各个特征之间的相关系数热力图：

def corr_mattrix():
    for j in range(1,4):    
        data_corr=data[data['企业唯一标识']==j][column_data[0:len(column_data)-1]].corr()#计算相关系数

        print(data_corr)

        #print(predict_corr)
        #根据相关系数来筛选特征变量
    #找寻K个特征与目标值最相关
        k=10
        cols=data_corr.nlargest(10,'在线人数')['在线人数'].index
        #print("cols.index",cols)
        cm=np.corrcoef(data_corr[cols].values.T)
        plt.figure(figsize=(10,10))
        hm=sns.heatmap(data_corr[cols].corr(),square=True,annot=True)
        print(cm)
        plt.show()
    predict_corr=predict[column_pre].corr()#计算相关系数
    cols=data_corr.nlargest(10,'在线人数')['在线人数'].index
        #print("cols.index",cols)
    cm=np.corrcoef(data_corr[cols].values.T)
    plt.figure(figsize=(10,10))
    hm=sns.heatmap(data_corr[cols].corr(),square=True,annot=True)
   # print(cm)
    plt.show()


corr_mattrix()

绘图结果如下：

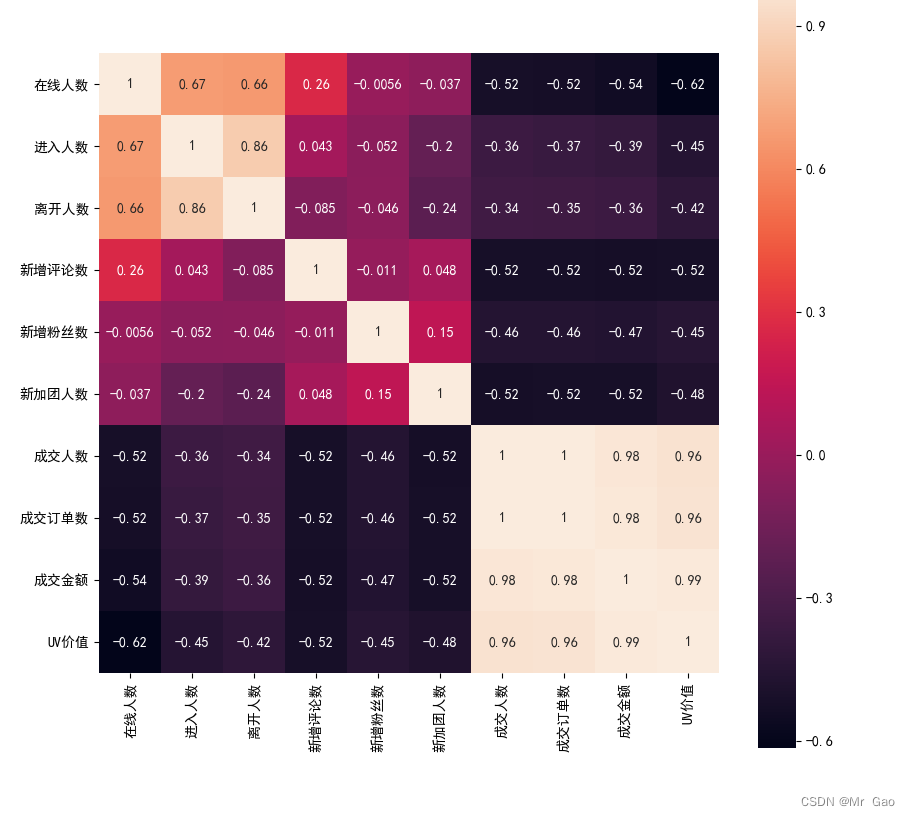
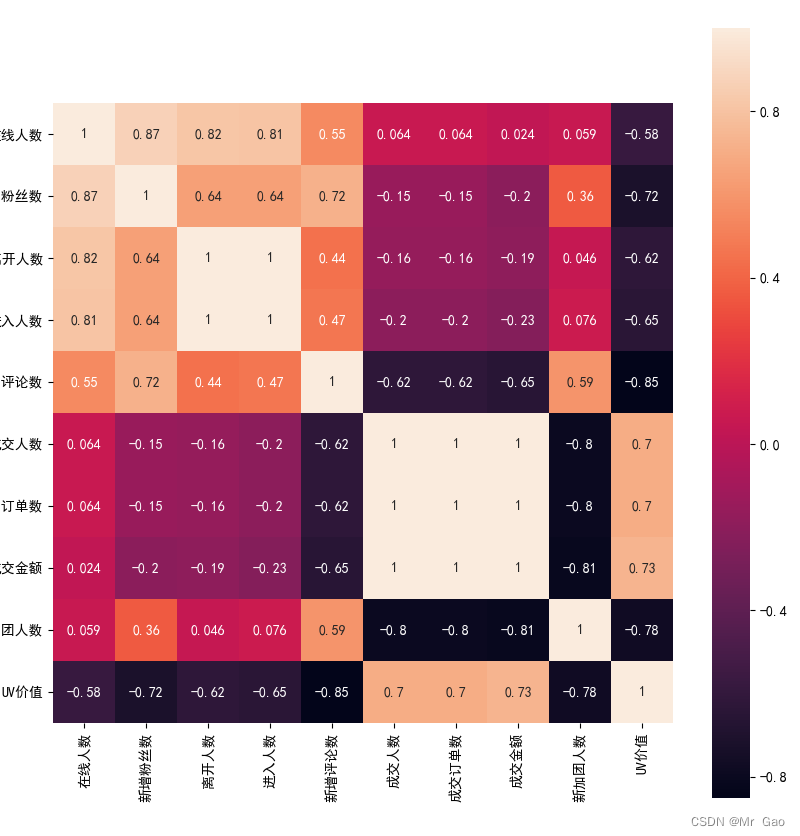
现在呢，我们使用arima模型对predict.csv进入直播间人数后几年数据进行预测：

import statsmodels.graphics.tsaplots as sm 
def draw_acf_and_pacf(serise,lag=20):
	# 绘图
	f = plt.figure()
	ax1 = f.add_subplot(211)
	sm.plot_acf(serise, lags=20, ax=ax1)

	ax2 = f.add_subplot(212)
	sm.plot_pacf(serise, lags=20, ax=ax2)
	plt.show()

draw_acf_and_pacf(predict["进入人数"][len(predict["进入人数"])-50:len(predict["进入人数"])])


model = ARIMA(predict["进入人数"][len(predict["进入人数"])-50:len(predict["进入人数"])], order=(3, 0, 3))
model_fit = model.fit()
forest= model_fit.forecast(10)
forest=list(forest)
y=list(predict["进入人数"])
y=y+forest
#y = np.append(y,forest)
x=list(range(len(y)))
   
plt.plot(x,y,lw=1,label='Arima model')
plt.legend()

plt.ylabel('进入人数')
plt.title("进入人数变化趋势图")
plt.show()

plt.plot(x[len(x)-50:len(x)],y[len(x)-50:len(x)],lw=1,label='Arima model')
plt.legend()
plt.xlabel('最后四十次进入人数和预测的十次')
plt.ylabel('进入人数')



plt.title("arima 模型预测结果图")
plt.show()

os.system("pause")

第一张图是自相关系数图和偏自相关系数图：

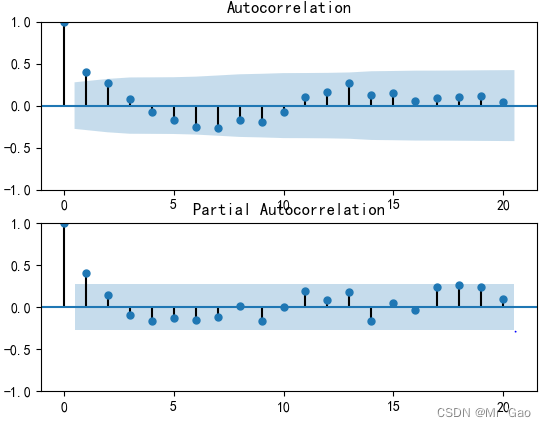
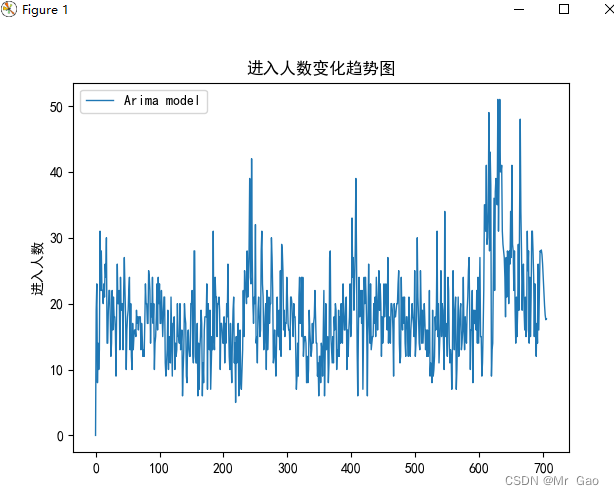
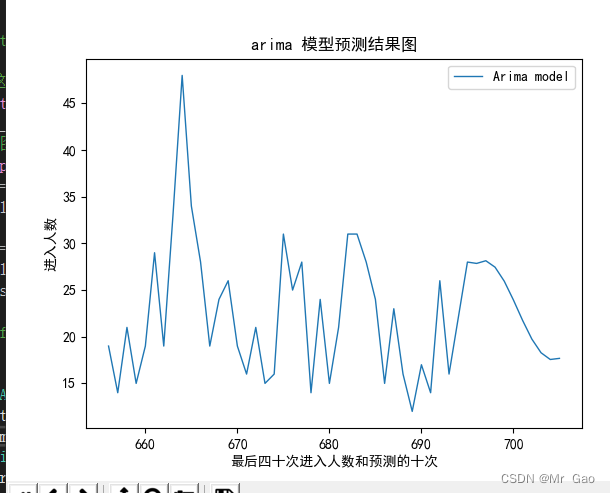
博主对于代码和数据分析方面相关的内同并没有太多介绍，需要你们自己去多花一些功夫哈。

本篇博客完整代码如下：
数据集，我已上传到我的资源里，修改一下路径即可运行代码。

#导入数据，编码方式为utf-8，每个字段的分割符为一个tab
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import os
import time
import statsmodels.api as sm
from scipy import stats
from statsmodels.tsa.arima.model import ARIMA
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题




name_data=['索引',"自然流量详情","付费流量详情","UV价值","新增评论数","时间","新增粉丝数","离开人数","新加团人数","成交金额","在线人数",
"进入人数","成交订单数","成交人数","企业唯一标识"]
name_predict=['索引',"自然流量详情","付费流量详情","UV价值","新增评论数","时间","新增粉丝数","离开人数","新加团人数","成交金额","在线人数",
"进入人数","成交订单数","成交人数"]
data=pd.read_csv(r"C:\Users\gaoxi\Desktop\data\data\data.csv",encoding="utf-8",names=name_data)
predict=pd.read_csv(r"C:\Users\gaoxi\Desktop\data\data\predict.csv",encoding="utf-8",names=name_predict)
#查看数据集的基本信息

print(data.columns)
print(data.info())
print(predict.info())

print(data.head())
print(predict.head())
#print(data["自然流量详情"])
#数据处理
#需要删除第一行
data=data.drop(index=0)
predict=predict.drop(index=0)

print(data.head())
print(predict.head())



#数据类型转化
column_data=data.columns.tolist()
remove=['索引',"自然流量详情","付费流量详情","时间"]

for i in remove:
        column_data.remove(i)
for i in column_data:
        data[i]=data[i].astype('float')
column_pre=predict.columns.tolist()

for i in remove:
        column_pre.remove(i)
for i in column_pre:
        predict[i]=predict[i].astype('float')
#时间格式类型转化      
data["时间"] = pd.to_datetime(data["时间"])

predict["时间"] = pd.to_datetime(predict["时间"])
#缺失值处理
print(data.info())
print(predict.info())
data=data.dropna()
print(data.info())

#print(data["时间"])
#因为只有data有缺失值，而且只有几条，所以我们可以进行直接删除，不影响后续数据分析
#异常值处理


#把所有特征的箱线图画出来




def plot1():
   
   
    #异常值是指远远偏离整个样本总体的观测值；异常值我们通常采用箱线图来处理，处在上下限之外的数据都都属于异常值
    for j in range(1,4):
        plt.figure(figsize=(80,60))
       
  
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(4,4,i+1)#将画布分割为6行8列
            sns.boxplot(data[data['企业唯一标识']==j][column_data[i]],orient="v",width=0.5)#每一个小区域画出箱型图
        #    plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel
    
    
        plt.show()

    plt.figure(figsize=(80,60))
   
 

    for i in range(len(column_pre)):
        plt.subplot(4,4,i+1)#将画布分割为6行8列
        sns.boxplot(predict[column_pre[i]],orient="v",width=0.5)#每一个小区域画出箱型图
       # plt.xlabel(column_pre[i],fontsize=12)#x轴的注释为xlabel
    
    plt.show()

    #经过箱型图分析，我们发现直播间各种流量箱型图都极为不稳定。所以可能，本身就不存在异常值，跟这个直播的性质有关，可能那天有个
    #比较著名的人突然来直播间就会带动各种流量，所以我们要特殊问题特殊分析，不需要进行异常值删除
plot1()

#

#数据分布分析
#直方图和QQ图
#QQ图是指数据的分位数和正态分布的分位数对比参照的图，如果数据符合正态分布，所有的点都会落在直线上。
#我们首先绘制V0变量的统计分布
def plot2():
    for j in range(1,4):
        plt.figure(figsize=(80,60))
        p=1
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(6,4,p)#将画布分割为6行8列
            p=p+1
   
            stats.probplot(data[data['企业唯一标识']==j][column_data[i]],plot=plt)
            plt.xlabel(' ')#x轴的注释为xlabel
            plt.title(" ")#x轴的注释为xlabel
            plt.subplot(6,4,p)
            p=p+1
            df=data[data['企业唯一标识']==j][column_data[i]]
            print(df)
            sns.distplot(df,fit=stats.norm)#fit=stats.norm代表标准正态分布
    
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

        plt.show()
    plt.figure(figsize=(80,60))
    p=1
    for i in range(len(column_pre)):
            plt.subplot(6,4,p)#将画布分割为6行8列
            p=p+1
    
   
            stats.probplot(predict[column_pre[i]],plot=plt)
            plt.xlabel(' ')#x轴的注释为xlabel
            plt.title(" ")#x轴的注释为xlabel
            plt.subplot(6,4,p)
            p=p+1
            sns.distplot(predict[column_pre[i]],fit=stats.norm)#fit=stats.norm代表标准正态分布
    
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

    plt.show()
plot2()

def plot3():
   
    for j in range(1,4):
        plt.figure(figsize=(80,60))
        plt.title("X轴为时间 Y轴为流量")
        p=1
        for i in range(len(column_data)):
            if column_data[i]=='企业唯一标识' :
              continue
            plt.subplot(3,4,p)#将画布分割为6行8列
            p=p+1
   
            plt.plot(data[data['企业唯一标识']==j]['时间'],data[data['企业唯一标识']==j][column_data[i]])
            plt.xlabel(' ',fontsize=5)#x轴的注释为xlabel
            plt.xticks(rotation=30)
      #      plt.title(column_data[i])#x轴的注释为xlabel
         
            #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

      #  plt.show()
  
    plt.figure(figsize=(80,60))
    p=1
    for i in range(len(column_pre)):
        plt.subplot(3,4,p)#将画布分割为6行8列
        p=p+1
    
        plt.plot(predict['时间'],predict[column_pre[i]])
        #stats.probplot(predict[column_pre[i]],plot=plt)
        plt.xlabel(' ')#x轴的注释为xlabel
        plt.xticks(rotation=30)
        plt.title(" ")#x轴的注释为xlabel
       # plt.subplot(6,4,p)
        #p=p+1
        #plt.xlabel(column_data[i],fontsize=12)#x轴的注释为xlabel

    plt.show()


plot3()


def corr_mattrix():
    for j in range(1,4):    
        data_corr=data[data['企业唯一标识']==j][column_data[0:len(column_data)-1]].corr()#计算相关系数

        print(data_corr)

        #print(predict_corr)
        #根据相关系数来筛选特征变量
    #找寻K个特征与目标值最相关
        k=10
        cols=data_corr.nlargest(10,'在线人数')['在线人数'].index
        #print("cols.index",cols)
        cm=np.corrcoef(data_corr[cols].values.T)
        plt.figure(figsize=(10,10))
        hm=sns.heatmap(data_corr[cols].corr(),square=True,annot=True)
        print(cm)
        plt.show()
    predict_corr=predict[column_pre].corr()#计算相关系数
    cols=data_corr.nlargest(10,'在线人数')['在线人数'].index
        #print("cols.index",cols)
    cm=np.corrcoef(data_corr[cols].values.T)
    plt.figure(figsize=(10,10))
    hm=sns.heatmap(data_corr[cols].corr(),square=True,annot=True)
   # print(cm)
    plt.show()


corr_mattrix()

#注意，这里要引入

import statsmodels.graphics.tsaplots as sm 
def draw_acf_and_pacf(serise,lag=20):
	# 绘图
	f = plt.figure()
	ax1 = f.add_subplot(211)
	sm.plot_acf(serise, lags=20, ax=ax1)

	ax2 = f.add_subplot(212)
	sm.plot_pacf(serise, lags=20, ax=ax2)
	plt.show()

draw_acf_and_pacf(predict["进入人数"][len(predict["进入人数"])-50:len(predict["进入人数"])])


model = ARIMA(predict["进入人数"][len(predict["进入人数"])-50:len(predict["进入人数"])], order=(3, 0, 3))
model_fit = model.fit()
forest= model_fit.forecast(10)
forest=list(forest)
y=list(predict["进入人数"])
y=y+forest
#y = np.append(y,forest)
x=list(range(len(y)))
   
plt.plot(x,y,lw=1,label='Arima model')
plt.legend()

plt.ylabel('进入人数')
plt.title("进入人数变化趋势图")
plt.show()

plt.plot(x[len(x)-50:len(x)],y[len(x)-50:len(x)],lw=1,label='Arima model')
plt.legend()
plt.xlabel('最后四十次进入人数和预测的十次')
plt.ylabel('进入人数')



plt.title("arima 模型预测结果图")
plt.show()

os.system("pause")