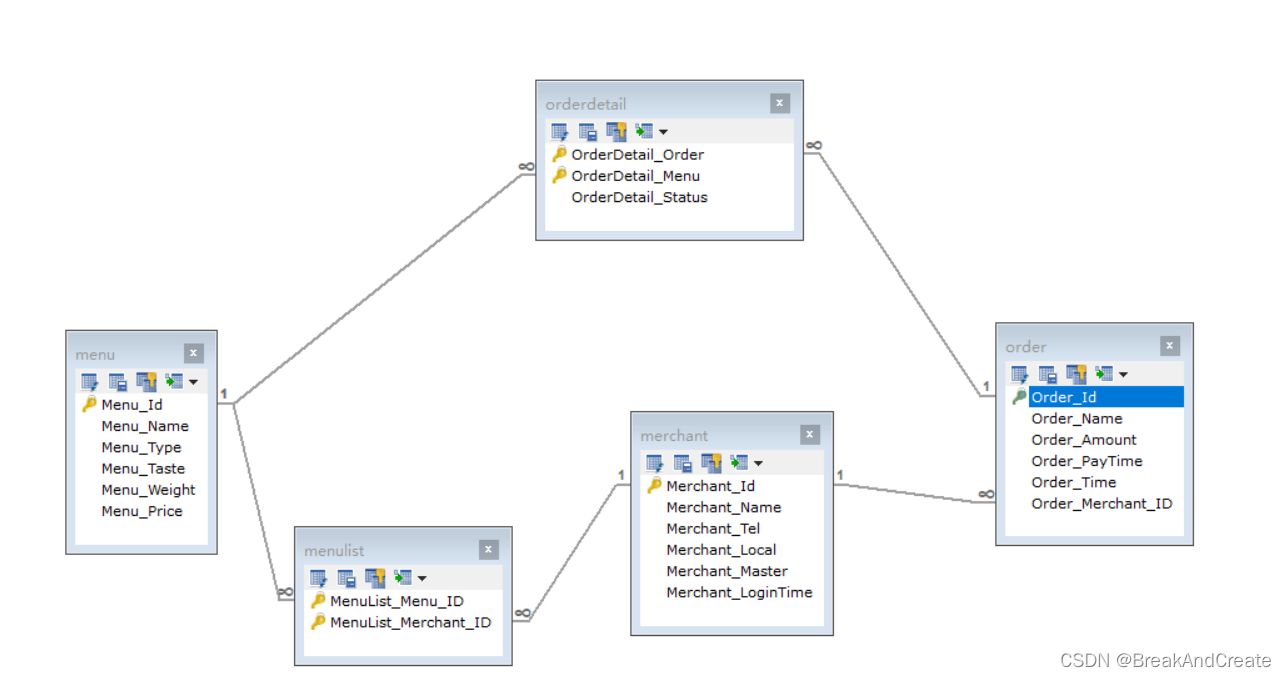
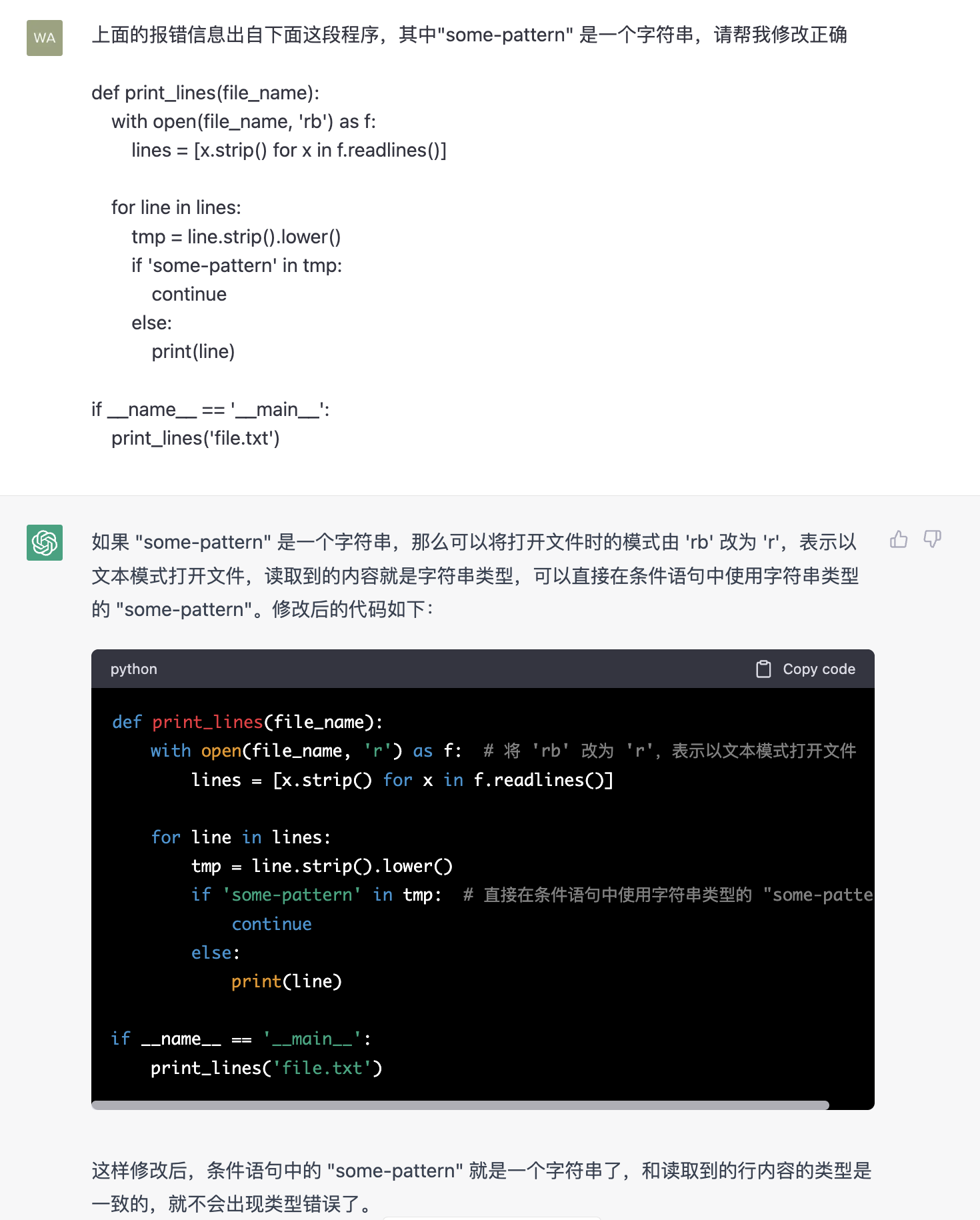
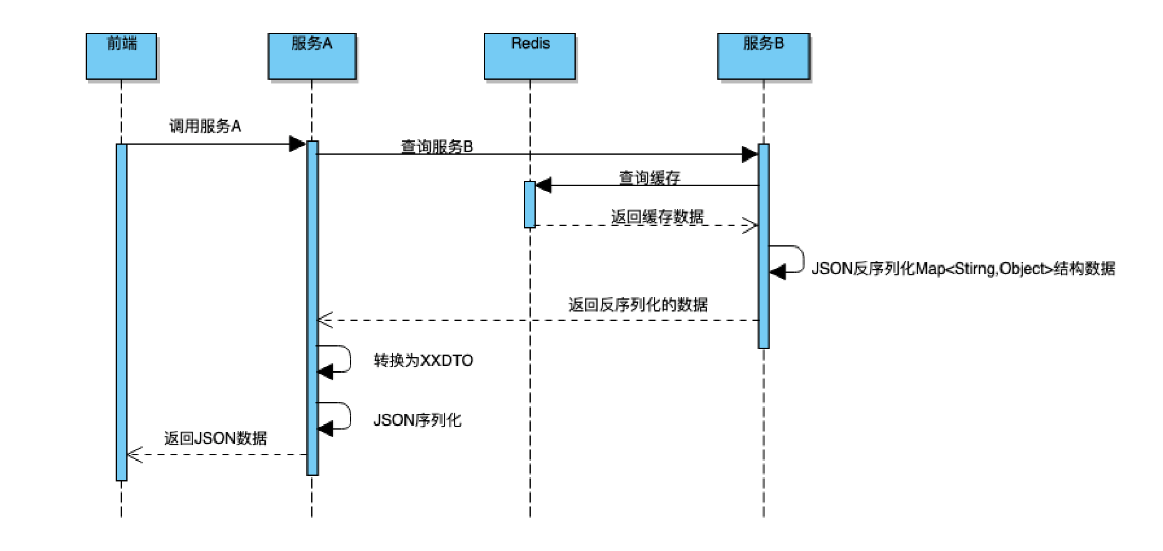
0. 简介
在我们之前接触的算法中,基本上都是要处理帧间雷达畸变的,类似于VSLAM系统,频率固定(例如10Hz), 而实际上,激光雷达点是按照不同的时间瞬间顺序采样的,将这些点累积到帧中会引入人工运动畸变,并且会对地图结果和里程计精度产生负面影响。低帧率还会增加里程计的延迟并限制可达带宽,其中里程计带宽类比于动态系统的带宽,即系统增益下降到0.707的频率。里程计带宽表示运动速度可以多快,里程计才能满意地进行估计。Mars实验室提出了《Point-LIO: Robust High-Bandwidth LiDAR-Inertial Odometry》这篇文章,Point-LIO能够在严重振动和激烈运动(高达75 rad/s的角速度)下提供准确的高频率里程计(4-8 kHz)和可靠的建图,超出了IMU测量范围。
1. 主要贡献
在这项工作中,我们通过两种关键的新技术解决了这些问题:点对点状态更新和随机过程增强的运动学模型。具体而言,我们的贡献如下:
- 提出了一种逐点(point-wise) LIO框架,该框架在实际采样时间融合激光雷达点,而不会累积到帧中。去除点累积消除了帧内运动失真,并允许以接近点采样率的高里程计输出和建图更新,这进一步使系统能够跟踪非常快的运动。
- 为了进一步提高系统带宽到超出IMU测量范围,用随机过程模型对IMU测量进行建模。将该模型扩展到系统运动学中,并将IMU测量值视为系统输出。即使IMU饱和,随机过程增强的运动学模型也可以平滑估计系统状态,包括角速度和线加速度。
- 将这两个关键技术集成到一个完全紧耦合的LIO系统中,称为Point-LIO。系统使用流形扩展卡尔曼滤波器通过在其各自的采样时间融合每个LiDAR点或IMU数据来更新系统状态。通过利用系统的稀疏性和线性,开发的系统即使在微型飞行器上基于低功耗ARM的计算机上也能实现实时状态估计。
- 开发的系统在由具有非常小FoV的新兴固态LiDAR收集的各种挑战性的现实世界数据中进行了测试。结果表明,Point-LIO具有运动畸变补偿能力,具有高里程计输出速率 (4-8 kHz) 和高带宽 (>150Hz) 的能力。该系统还能够在初始阶段后通过饱和IMU测量来估计极端激进运动 (角速度大于75 rad/s) 下的状态。此外,对来自各种公开LiDAR数据集的12个序列的详尽基准比较表明,Point-LIO实现了与其他方法一致可比的准确性和效率,同时花费更少的计算资源。最后演示了实际无人机上的实际应用。
2. 系统综述
本文设计理念是根据以下两点得出的:
1)激光雷达点是按照各自的时间顺序采样的,而不是在同一时间采样的帧;
2)IMU数据是系统的测量,而不是输入。
一旦接收到各自的测量(每个激光雷达点或IMU数据),我们在基于流形的扩展卡尔曼滤波框架[55]中融合这两个测量。我们设计的系统概述如图1所示,按顺序采样的激光雷达点和IMU数据都用于在它们各自的时间戳上更新状态,从而实现极高速率的里程计输出,即实际上为4-8 kHz。特别地,对于每个接收到的激光雷达点,我们会从地图中搜索相应的平面。如果该点与地图中点拟合的平面匹配,则计算残差以使用基于流形的卡尔曼滤波器更新系统状态。最终优化的姿态将激光雷达点注册到全局坐标系并合并到地图中,然后继续下一次测量(激光雷达点或IMU数据)。否则,如果该点没有匹配的平面,则通过卡尔曼滤波器预测的姿态直接添加到地图中。为了同时实现快速平面对应搜索和允许新注册点的加入,我们使用了增量k-d树结构ikd-Tree,该结构最初是在FAST-LIO2 [29]中开发的。对于每个IMU测量,会分别进行饱和检查,对于具有饱和值的通道不会用于状态更新。
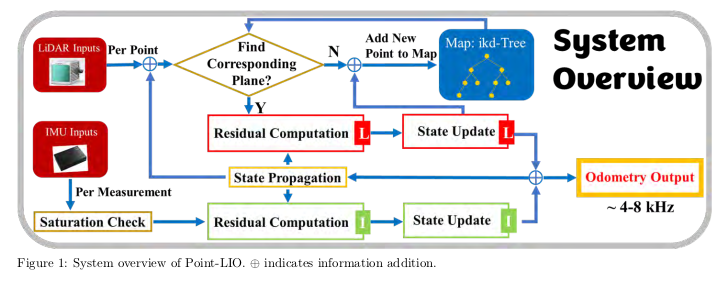
图1:Point-LIO系统概述。⊕表示信息添加。
3. 符号说明
Point-LIO的状态估计是一个紧耦合的基于流形的卡尔曼滤波器。在这里,我们简要介绍滤波器的基本公式和工作流程,并参考[55]提供更详细和理论性的基于流形的卡尔曼滤波器解释。
为了方便说明,我们采用以下符号:

此外,我们引入两个封装操作 ⊞ ⊞ ⊞(“boxplus”)和其逆 ⊟ ⊟ ⊟(“boxminus”),在[55]中定义,用于描述维度为 n n n的流形 M M M上的系统,并在欧几里得空间 R n \mathbb{R}^n Rn中参数化状态误差。同时,这些操作可以更紧凑地描述离散时间中的系统状态空间模型。我们参考[55]提供更详细的定义和推导。在本文中,我们只关注流形 S O ( 3 ) SO(3) SO(3)和 R n \mathbb{R}^n Rn:
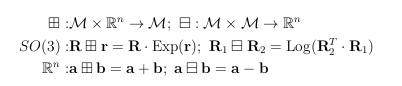
其中,$Exp®= I + sin(∥r∥)\frac{|r|}{∥r∥} + (1 − cos(∥r∥))∕\frac{|r|2}{∥r∥2} 是 是 是SO(3) 上的指数映射, 上的指数映射, 上的指数映射,Log 是其逆映射。对于一个复合流形 是其逆映射。对于一个复合流形 是其逆映射。对于一个复合流形M = SO(3) × \mathbb{R}^n ,它是两个子流形 ,它是两个子流形 ,它是两个子流形M = SO(3)$ 和 R n \mathbb{R}^n Rn的笛卡尔积,我们有:
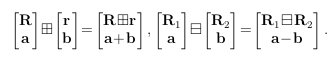
4. 运动学模型
我们首先推导系统模型,它由状态转移模型和测量模型组成。
4.1 状态转移模型 (与Fast-LIO2类似)
以IMU坐标系(表示为I)作为机体坐标系,以第一个IMU坐标系作为全局坐标系(表示为G),连续的运动学模型为:
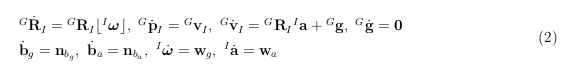
其中, G R I ^GR_I GRI, G p I ^G p_I GpI和 G v I ^G v_I GvI表示IMU在全局坐标系中的姿态、位置和速度, G g ^G g Gg表示全局坐标系中的重力向量。 b g b_g bg和 b a b_a ba是由高斯噪声驱动的随机漂移IMU偏差,分别为 n b g ∼ N ( 0 , Q b g ) n_{b_g} ∼ N(0, Q_{b_g} ) nbg∼N(0,Qbg)和 n b a ∼ N ( 0 , Q b a ) n_{b_a} ∼ N(0, Q_{b_a} ) nba∼N(0,Qba)。符号 ⌊ a ⌋ ⌊a⌋ ⌊a⌋是 a ∈ R 3 a ∈ \mathbb{R}^3 a∈R3的反对称叉积矩阵。 I ω I_ω Iω和 I a I_a Ia表示IMU在机体坐标系即IMU坐标系中的角速度和加速度。正如[14]所提出的,某些机器人运动(角速度 I ω I_ω Iω和线性加速度 I a I_a Ia)总是可以视为信号集合或群体的样本,这使我们能够通过随机过程在统计上描述机器人运动。此外,正如[14]所建议的那样,由于机器人系统的运动通常具有一定的平滑性(例如,由于执行器延迟),角速度和加速度的快速变化相对不太可能,因此N阶积分器随机过程通常足以实际使用。特别地,我们选择由高斯噪声 w g ∼ N ( 0 , Q g ) w_g ∼ N(0, Q_g ) wg∼N(0,Qg)和 w a ∼ N ( 0 , Q a ) w_a ∼ N(0, Q_a ) wa∼N(0,Qa)驱动的一阶积分器模型来分别模拟角速度 I ω I_ω Iω和线性加速度 I a I_a Ia。
然后,在每个测量步骤 k k k处离散化连续模型(2)。将 ∆ t k ∆t_k ∆tk表示为当前测量间隔,它是前一个测量(IMU数据或LiDAR点)和当前测量(IMU数据或LiDAR点)之间的时间差。通过假设输入在间隔 ∆ t k ∆t_k ∆tk中保持不变,将连续模型(2)离散化,导致

其中,流形 M M M、函数 f f f、状态 x x x和过程噪声 w w w的定义如下:
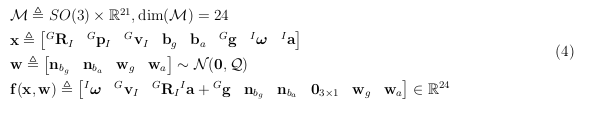
其中, Q = d i a g ( Q b g , Q b a , Q g , Q a ) Q = diag(Q_{b_g},Q_{b_a},Q_g,Q_a) Q=diag(Qbg,Qba,Qg,Qa)是过程噪声 w w w的协方差矩阵。
4.2 测量模型 (重点)
该系统有两个测量,一个LiDAR点或一个IMU数据(包括角速度和加速度测量)。这两个测量通常在不同的时间被系统采样和接收,因此我们将它们分别建模。 假设LiDAR坐标系与机体(即IMU)坐标系重合或具有预校准的外参,则LiDAR点 I p m k ^Ip_{m_k} Ipmk等于在本地IMU坐标系中的真实位置 I p k g t ^Ip^{gt}_k Ipkgt,该位置是未知的,受到加性高斯噪声 n L k ∼ N ( 0 , R L k ) n_{L_k} ∼ N(0, R_{L_k}) nLk∼N(0,RLk)的污染:

将该真实点使用真实(但未知)的IMU位姿 G T I k = ( G R I k , G p I k ) ^GT_{Ik} = (^GR_{Ik},^Gp_{Ik}) GTIk=(GRIk,GpIk)投影到全局坐标系后,应该正好位于地图中的一个局部小平面补丁上(参见图2),即:
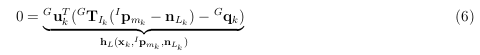
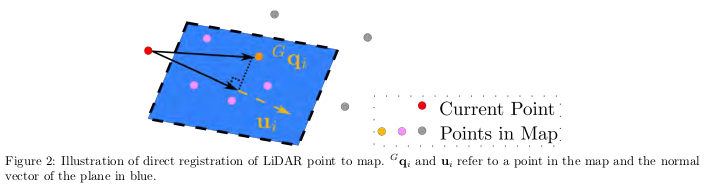
图2:LiDAR点直接注册到地图的示意图。蓝色表示平面的向量。 G q i ^Gq_i Gqi和 u i u_i ui表示地图中的一个点和法线。
其中, G u k ^Gu_k Guk是相应平面的法向量, G q k ^Gq_k Gqk是位于平面上的任意点。请注意, G T I k ^G T_{I_k} GTIk 包含在状态向量 x k x_k xk 中。(6)对状态向量 x k x_k xk 引入了隐式的测量模型。
IMU测量由角速度测量( I ω m ^Iω_m Iωm)和加速度测量( I a m ^Ia_m Iam)组成:

其中 n g ∼ N ( 0 , R g ) , n a ∼ N ( 0 , R a ) n_g ∼ N (0, R_g ),n_a ∼ N (0, R_a ) ng∼N(0,Rg),na∼N(0,Ra)均为高斯噪声。 n I = [ n g T n a T ] T ∼ N ( 0 , R I ) = N ( 0 , d i a g ( R g , R a ) ) n_I = [n^T_g n^T_a]^T ∼ N (0, R_I ) = N (0, diag(R_g , R_a )) nI=[ngTnaT]T∼N(0,RI)=N(0,diag(Rg,Ra))表示IMU的测量噪声。可以看出,在角速度测量 ω m ω_m ωm(或加速度测量 a a a)中,两个状态 ω ω ω, b g b_g bg(以及类似地 a a a, b a b_a ba)在状态方程(2)中是分开的,但现在是相关的。
综上所述,系统的测量模型可以用以下紧凑形式表示:

5. 扩展卡尔曼滤波器
点云-激光惯性导航系统使用紧耦合的扩展卡尔曼滤波器进行状态估计。本节介绍EKF的工作流程。
5.1 状态传播
假设我们已经收到了 k k k步的测量,并且在那个时间步骤上更新的状态为 x ˉ k x̄_k xˉk,更新的协方差矩阵为 P ˉ k P̄_k Pˉk。从第 k k k步到下一个测量步骤 k + 1 k + 1 k+1的状态传播直接遵循方程(3)中的状态转移模型,将 w k w_k wk设置为0:

协方差矩阵的传播方式为:

其中 Q k Q_k Qk是过程噪声 w k w_k wk的协方差,矩阵 F x k F_{x_k} Fxk, F w k F_{w_k} Fwk计算如下:

其中, x k + 1 x_{k+1} xk+1 是时间步 k + 1 k+1 k+1 的状态向量的真值, F 11 = E x p ( − I w ~ k ∆ t k ) F_{11} = Exp(- ^I\tilde{w}_k ∆t_k) F11=Exp(−Iw~k∆tk), F 31 = − G R ˉ I k ⌊ I a ˉ k ⌋ ∆ t k F_{31} = -^G R̄_{I_k} ⌊^I ā_k⌋∆t_k F31=−GRˉIk⌊Iaˉk⌋∆tk, F 38 = G R ˉ I k ∆ t k F_{38} = ^G R̄_{I_k} ∆t_k F38=GRˉIk∆tk。
5.2 残差计算 LiDAR测量:(重点)
雷达测量:根据Kalman传播(9)中的预测姿态 G T ^ I k + 1 = ( G R ^ I k + 1 , G p ^ I k + 1 ) ^G T̂_{I_{k+1}} =(^G R̂_{I_{k+1}},^Gp̂_{I_{k+1}}) GT^Ik+1=(GR^Ik+1,Gp^Ik+1),将测量的LiDAR点 I p m k + 1 ^I p_{m_{k+1}} Ipmk+1 投影到全局坐标系中的 G p ^ k + 1 = G R ^ I k I p m k + 1 + G p ^ I k + 1 ^Gp̂_{k+1} = ^GR̂_{I_k} ^I p_{m_k+1} + ^G p̂_{I_{k+1}} Gp^k+1=GR^IkIpmk+1+Gp^Ik+1,并在由ikd-Tree组织的地图中搜索其最近的5个点(距离 G p ^ k + 1 ^G p̂_{k+1} Gp^k+1 不超过5 m)。然后,使用找到的最近邻点来拟合局部小平面补丁,其法向量为 G u k + 1 ^G u_{k+1} Guk+1,重心为 G q k + 1 ^G q_{k+1} Gqk+1,如测量模型所示(参见方程(6)和图2)。如果最近的5个点不在拟合的平面路径上(即,任何点到平面的距离大于0.1 m),则当前的LiDAR点 G p ^ k + 1 ^G p̂_{k+1} Gp^k+1 的测量直接合并到地图中,无需进行残差计算或状态更新。否则,如果局部平面拟合成功,则根据方程(8)计算残差( r L k + 1 r_{L_{k+1}} rLk+1)。
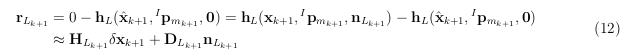
其中, δ x k + 1 = x k + 1 ⊟ x ^ k + 1 δx_{k+1} = x_{k+1} ⊟ x̂_{k+1} δxk+1=xk+1⊟x^k+1,其中 x k + 1 x_{k+1} xk+1 是时间步 k + 1 k+1 k+1 的状态向量的真值, x ^ k + 1 x̂_{k+1} x^k+1 是时间步 k + 1 k+1 k+1 的状态向量的估计值。
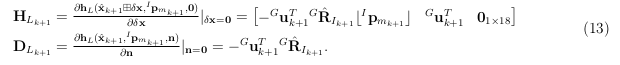
IMU测量:通过检查当前测量值与额定测量范围之间的差距来判断IMU测量通道是否被丢弃。如果差距太小,则该IMU测量通道将被丢弃而不会更新状态。然后,收集未饱和IMU通道的加速度和角速度测量值,根据方程(7)计算IMU残差( r I k + 1 r_{I_{k+1}} rIk+1)(为简化符号,我们在此处使用所有六个通道的测量值)。
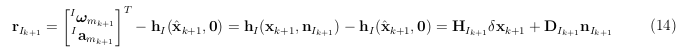
其中, δ x k + 1 = x k + 1 ⊟ x ^ k + 1 δx_{k+1} = x_{k+1} ⊟ x̂_{k+1} δxk+1=xk+1⊟x^k+1,其中 x k + 1 x_{k+1} xk+1 是时间步 k + 1 k+1 k+1 的状态向量的真值, x ^ k + 1 x̂_{k+1} x^k+1 是时间步 k + 1 k+1 k+1 的状态向量的估计值。
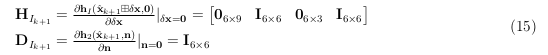
总之,来自LiDAR点测量(公式12)或IMU测量(公式14)的残差与状态 x k+1 和相应的测量噪声之间的关系如下:
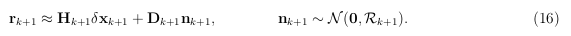



![[数据库系统] 三、简单查询](https://img-blog.csdnimg.cn/img_convert/7d47bc016435f2b02b5bea8438ae482b.png)