蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下G. Hits Different!

上绿名喽！

===========================================================================================

G. Hits Different

题目描述

In a carnival game, there is a huge pyramid of cans with 2023 rows, numbered in a regular pattern as shown.

If can $9^2$ is hit initially, then all cans colored red in the picture above would fall.

You throw a ball at the pyramid, and it hits a single can with number $n^2$. This causes all cans that are stacked on top of this can to fall (that is, can $n^2$ falls, then the cans directly above $n^2$ fall, then the cans directly above those cans, and so on). For example, the picture above shows the cans that would fall if can $9^2$ is hit.

What is the sum of the numbers on all cans that fall? Recall that $n^2=n\times n$.

Input

The first line contains an integer $t(1\le t\le 1000)$ — the number of test cases.

The only line of each test case contains a single integer $n(1\le n\le 10^6)$ — it means that the can you hit has label $n^2$.

Output

For each test case, output a single integer — the sum of the numbers on all cans that fall.

Please note, that the answer for some test cases won’t fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++). For all valid inputs, the answer will always fit into 64-bit integer type.

Example

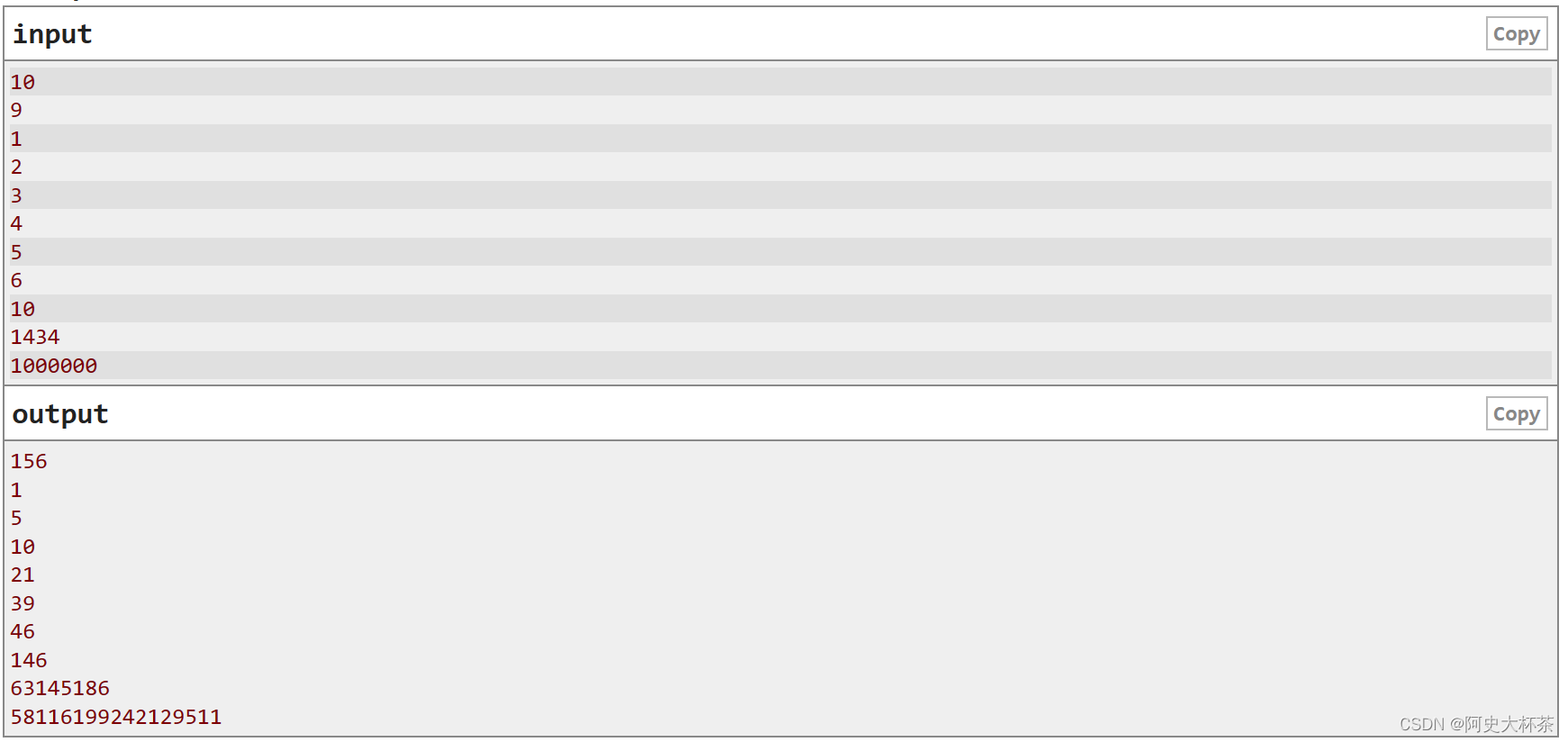
Note
The first test case is pictured in the statement. The sum of the numbers that fall is
$$1^2+2^2+3^2+5^2+6^2+9^2=1+4+9+25+36+81=156.$$
In the second test case, only the can labeled $1^2$ falls, so the answer is $1^2=1$.
In the third test case, the cans labeled $1^2$ and $2^2$ fall, so the answer is $1^2+2^2=1+4=5$.
In the fourth test case, the cans labeled $1^2$ and $3^2$ fall, so the answer is $1^2+3^2=1+9=10$.
In the fifth test case, the cans labeled $1^2,2^2$, and $4^2$ fall, so the answer is $1^2+2^2+4^2=1+4+16=21.$

思路

本题可以想到动态规划，我们可以这样考虑：

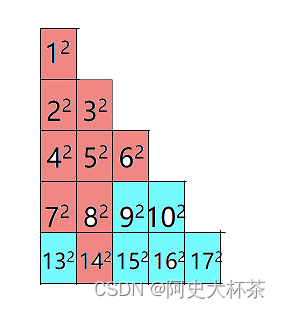
假设砸$14^2$这个点，我们看一下怎么转移：

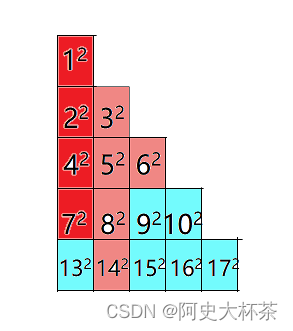
红色的是$14^2$左边这个点$7^2$这个点所能波及到的点

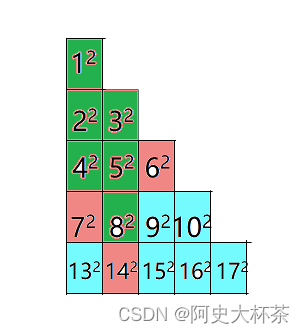
绿色的是$14^2$右边的点$8^2$所能波及到的点

然后我们看一下他们重复了那些点：

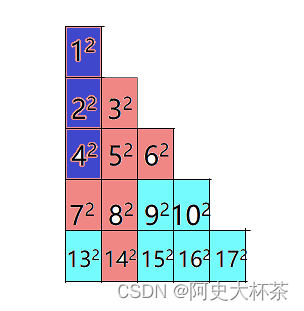
其实就是$14^2$上一行的上一行的左边的点$4^2$所能波及到的点

故此，砸$14^2$的值应该是砸$7^2$的值+砸$8^2$的值-砸$4^2$的值+$14^2$

可以推导出状态转移方程：（$dp[i][j]$表示砸图中第i行第j列的点的答案）
$$dp[i][j]=dp[i-1][j]+dp[i-1][j-1]-dp[i-2][j-1]+num[i][j]$$

其中，$num[i][j]$表示图中第i行第j列的数字

本题就是求$dp[1-2023][1-2023]$的值
时间复杂度$O(n^2)$

题中是输入的$n$我们找到他是第几行，第几列即可！

代码

#include <iostream>
#define int long long

using namespace std;

const int N = 2024;

int dt;
int n;
int dp[N][N];
int num[N][N];
int sum[N];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);
	
	int t = 1;
	for (int i = 1; i <= 2023; i ++)
		for (int j = 1; j <= i; j ++)
			num[i][j] = t * t, t ++;
			
	sum[1] = 1;
	for (int i = 2; i <= 2023; i ++)
		sum[i] = sum[i - 1] + i - 1;
	
	dp[1][1] = 1;
	for (int i = 2; i <= 2023; i ++)
		for (int j = 1; j <= i; j ++)
			dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] - dp[i - 2][j - 1] + num[i][j];
	
	cin >> dt;
	
	while (dt --)
	{
		cin >> n;
		
		int h;
		for (int i = 1; i <= 2023; i ++)
			if (n < sum[i])
			{
				h = i - 1;
				break;
			}
		
		cout << dp[h][n - sum[h] + 1] << endl;
	}
	
	return 0;
}