目录

一、Nyquist稳定判据

1）开环传递函数中没有积分环节（不含s=0的极点）

2）开环传递函数中含有积分环节（含s=0的开环极点）

二、Bode 稳定判据

---

稳定的定义： 任何系统在扰动的作用下都会偏离原平衡状态产生初始偏差。所谓 稳定性 就是指当扰动消除后，由初始状态恢复原平衡状态的能力；若系统可恢复平衡状态，则称系统是稳定的，否则是不稳定的。

稳定的充分必要条件： 系统的特征根都具有负实部。

时域稳定判据： 劳斯判据，霍尔维茨判据

频域稳定判据 ： Nyquist 判据（奈氏判据）， Bode 判据

Nyquist 判据是利用开环幅相特性曲线（ Nyquist 图）判断闭环稳定性的图解方法；

Bode 判据是利用开环对数频率特性曲线（ Bode 图）判断系统闭环稳定性的图解方法；

以上两判据均可用于判断闭环系统的 绝对稳定性 ，也能计算系统的 相对稳定指标 和研究改善系统性能的方法

---

一、Nyquist稳定判据

F(s)的特点：F(s)的零点就是控制系统的闭环极点；

                   F(s)的极点就是控制系统的开环极点。

思想：利用图解的方法来确定F(s)位于s右半平面的零点（控制系统的闭环极点），从而归纳出判别系统稳定性的奈氏判据。

分两种情况考虑:

  1）开环传递函数中没有积分环节（即s=0的开环极点）；

  2）开环传递函数中含有积分环节（即s=0的开环极点）。

---

1）开环传递函数中没有积分环节（不含s=0的极点）

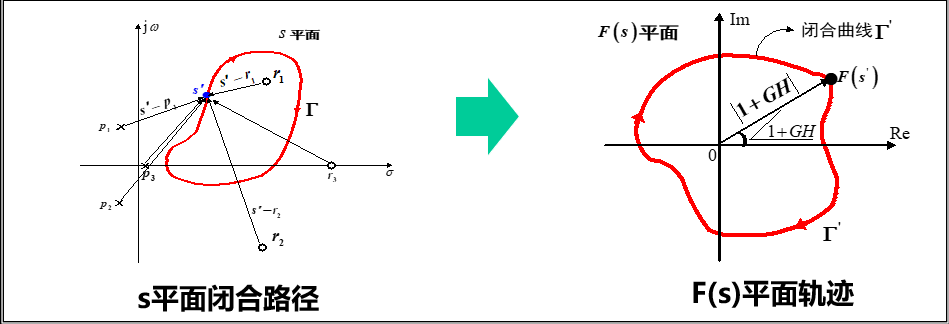
辐角原理（柯西定理、映射定理）：    若F(s)在s平面上除了有限个奇点外，它总是解析的，则当动点s’在s平面上顺时针方向绕不通过任何极点和零点的封闭曲线一周时，F(s)也在复平面上映射出一条闭合曲线

当沿路径  顺时针移动一周时，未被包围的零、极点对应的向量的净相角变化等于零。   

1. 若系统开环稳定，则闭环稳定的充要条件是：当w从-¥ ® +¥连续变化时，F(jw)=1+G(jw)曲线顺时针包围原点0圈，即奈氏曲线不包围(-1, j0)点。

2. 若系统有P个开环右根，则闭环稳定的充要条件是：当w从   -¥ ® +¥连续变化时，F(jw)=1+G(jw)曲线顺时针包围原点    -P圈，即奈氏曲线逆时针包围(-1, j0)点P圈。

        Note：①系统不含积分环节（无s=0开环极点）；②纯虚根归为开环左根。

---

2）开环传递函数中含有积分环节（含s=0的开环极点）

因此，若开环传递函数中含有1个积分环节（极点s=0），则奈氏曲线应该顺时针补画由0-→0+的180°、半径为无穷大的圆弧。

补圆原则:开环传递函数中含有n个积分环节，奈氏曲线应该顺时针补画ω由0-→0+的n/2个半径为无穷大的圆周。

Note：s=0视为开环左根

条件稳定系统: K 取特定值时，才稳定的系统；

结构不稳定系统: K 取任何值，均不稳定的系统。

---

二、Bode 稳定判据

奈氏曲线正负穿越负实轴的概念：

        上→下：正穿越（增大了相角）；

        下→上：负穿越（减小了相角）。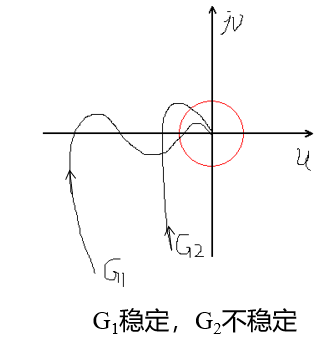

奈氏稳定判据：Nyquist曲线在（-∞，-1）正负穿越次数相等，则系统闭环稳定。

Bode稳定判据：

1、若系统开环稳定，则闭环稳定的充要条件是：在Bode图的L(w)>0频段，q(w) 正负穿越-180°线的次数相等。

2、若系统有P个开环右根，则闭环稳定的充要条件是： 在Bode图的L(w)>0频段，q(w) 对-180°线的净穿越（正减负）次数为P/2。   

         Note：①从-180°开始的穿越计为1/2次；

                     ②若系统开环传递函数有n 个积分环节，则应补画从q(0+)+n *90 ° 到q(0+)的虚线，并将其视为q(w)的一部分。