引入
分治算法(divide and conquer)是五大常用算法(分治算法、动态规划算法、贪心算法、回溯法、分治界限法)之一。其实,很多人在平时学习中已经不知不觉就用到了分治算法,只是不知道那就是分治算法,今天,我们就来全面地去认识和了解分治算法。
在学习分治算法之前,问你一个问题,相信大家小时候都有存钱罐的经历,父母亲人如果给钱都会往自己的宝藏中存钱,我们每隔一段时间都会清点清点钱。但是一堆钱让你处理起来你可能觉得很复杂,因为数据相对于大脑有点庞大了,并且很容易算错,你可能会将它 先分 成几个小份算,然后 再叠加 起来计算总和就获得这堆钱的总数了。
image-20201130124009617
当然如果你觉得各个部分钱数量还是太大,你依然可以进行划分然后合并,我们之所以这么多是因为:计算每个小堆钱的方式和计算最大堆钱的方式是相同的(区别在于体量上)然后大堆钱总和其实就是小堆钱结果之和。这样其实就有一种分治的思想。当然这些钱都是想出来的……
分治算法的思想
分治算法是用了分治思想的一种算法,什么是分治?
分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在计算机科学中,分治法就是运用分治思想的一种很重要的算法。分治法是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)等等。
将父问题分解为子问题同等方式求解,这和递归的概念很吻合,所以在分治算法通常以递归的方式实现(当然也有非递归的实现方式)。分治算法的描述从字面上也很容易理解,分、治其实还有个合并的过程:
· 分(Divide):递归解决较小的问题(到终止层或者可以解决的时候停下)
· 治(Conquer):递归求解,如果问题够小直接求解。
· 合并(Combine):将子问题的解构建父类问题
一般分治算法在正文中分解为两个即以上的递归调用,并且子类问题一般是不想交的(互不影响)。当求解一个问题规模很大很难直接求解,但是规模较小的时候问题很容易求解并且这个问题并且问题满足分治算法的适用条件,那么就可以使用分治算法
那么采用分治算法解决的问题需要 满足那些条件(特征) 呢?
1 . 原问题规模通常比较大,不易直接解决,但问题缩小到一定程度就能较容易的解决。
2 . 问题可以分解为若干规模较小、求解方式相同(似)的子问题,且子问题之间求解是独立的互不影响。
3 . 合并问题分解的子问题可以得到问题的解。
你可能会疑惑分治算法和递归有什么关系?其实分治重要的是一种 思想 ,注重的是 问题分、治、合并的过程。而分治中的递归是一种方式(工具),这种方式通过函数自己调用自己,但是通过修改函数的参数来达到将问题分解、使问题规模变小的目的。
分治算法经典问题
对于分治算法的经典问题,重要的是其思想,因为我们大部分借助递归去实现,所以在代码实现上大部分都是很简单。分治算法的经典问题,个人将它分成两大类:子问题完全独立和子问题不完全独立。
1 . 子问题完全独立就是原问题的答案可完全由子问题的结果推出。
2 . 子问题不完全独立,有些 区间类的问题或者跨区间问题 使用分治可能结果跨区间,在考虑问题的时候需要仔细借鉴下。
分治算法解决问题主要有三个步骤:
Divide(切分子问题的方案)
Conquer(一般子问题独立相同的,所以这里一般是递归的解决子问题)
Combine(子问题提升至更大问题的时候需要对子问题的解决方案进行合并)
分治算法对待不同的问题需要不同的分治方案,所以掌握缩小问题的规模的思想是非常重要的,比较高级的动态规划和贪心也都是通过缩小问题规模来提升时间复杂度的。所以通过练习,多掌握一些具体实例的分治方案,这样碰到陌生问题的时候可以像熟悉的问题靠拢,这样才容易解决陌生的问题。
二分查找(搜索)——P2499 二分递归查找(search)
二分搜索是分治的一个实例,只不过二分搜索有着自己的特殊性
序列是有序
的结果为一个值
正常二分将一个完整的区间分成两个区间,两个区间本应单独找值然后确认结果,但是通过有序的区间可以直接确定结果在哪个区间,所以分的两个区间只需要计算其中一个区间,然后继续进行一直到结束。实现方式有递归和非递归,但是非递归(while循环)用的更多一些。
方法一:递归二分
二分查找即可,分左中右三段判断
#include <bits/stdc++.h>
using namespace std;
int a[1000], n, k;
int search(int l, int r)
{
if(l >= r) // 搜到头了,返回结果
return a[l]==k?l:-1;
int mid = l+r>>1;
if(a[mid] == k) // 搜到了
return mid;
else if(a[mid]>k)
return search(l, mid-1); // 在左半边,搜
else
return search(mid+1, r); // 在右半边,搜
}
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i++)
cin >> a[i];
cout << search(1,n);
return 0;
}
方法二、循环二分
题目要求用递归实现,这是出于学习递归二分的目的,本题也可以用循环二分实现,定义 二分中的三个关键变量 int l, r, mid; 循环查找区域即可。
#include <bits/stdc++.h>
using namespace std;
int a[1000], n, k;
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i++)
cin >> a[i];
int l = 1, r = n, mid; // 初始二分范围
while(l <= r)
{
mid = l+r>>1; // 二分
if(a[mid] > k) // 查找左半边
r = mid-1;
else if(a[mid] == k) // 中间,找到就返回
{
cout << mid;
return 0;
}
else // 右半边
l = mid+1;
}
cout << -1;
return 0;
}
方法三、暴力枚举
因为数据范围太小了,本题也可以用暴力枚举去直接循环查找,但是......弱爆了,如果数据范围达到 10^8级别以上,就会超时了
#include<bits/stdc++.h>
using namespace std;
long long n,k,a[1001],b[1001],flag=1;
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]==k)
{
cout<<i;
flag=0;
}
}
if(flag==1)
{
cout<<-1;
}
return 0;
}
方法四:另辟蹊径
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,k,s=0;
cin>>n>>k;
for(int i=1;i<=n;i++)
{
int t;
cin>>t;
if(t==k)
{
s=i;
}
}
cout<<(s==0?-1:s);
}
归并排序
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分而治之
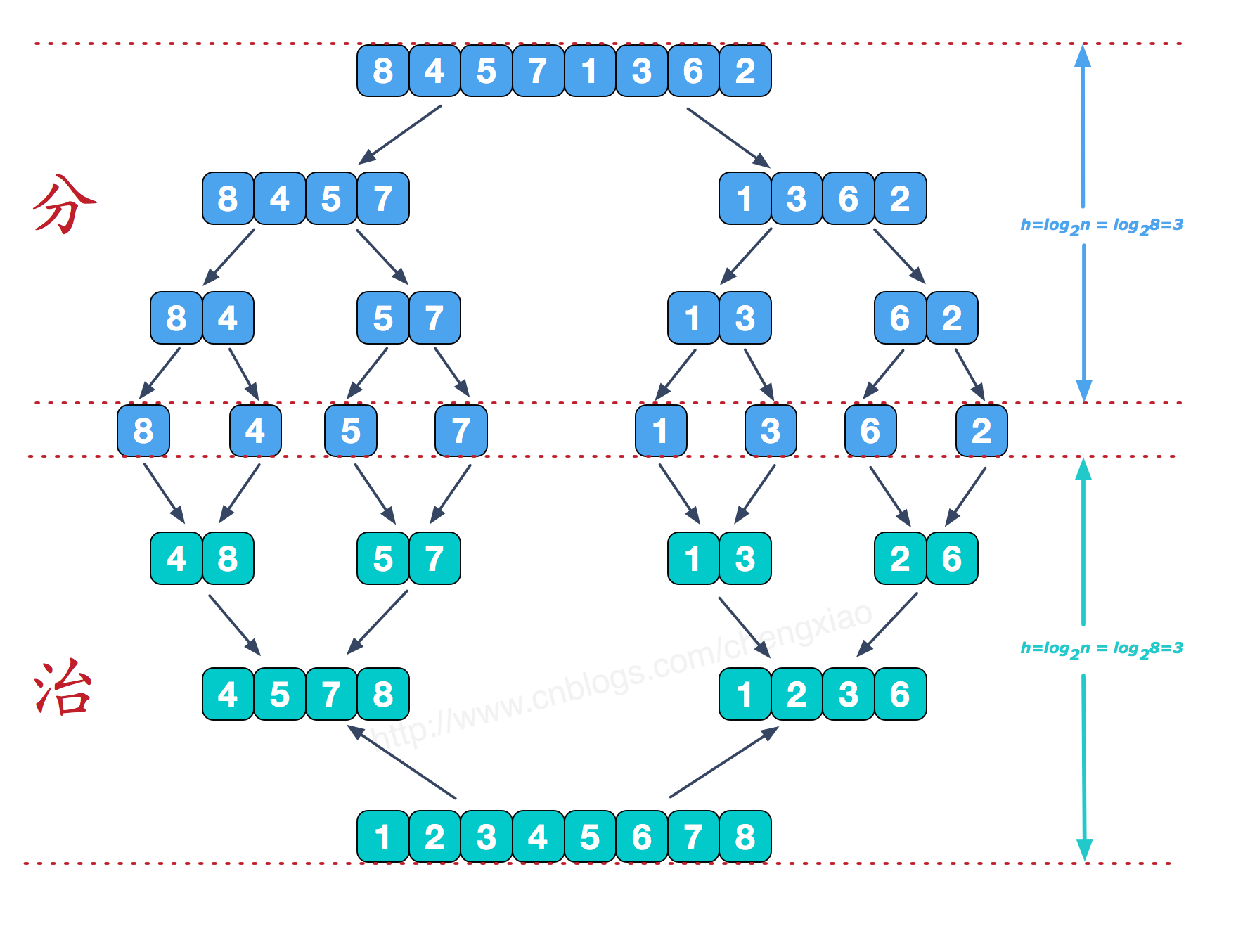
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并相邻有序子序列
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
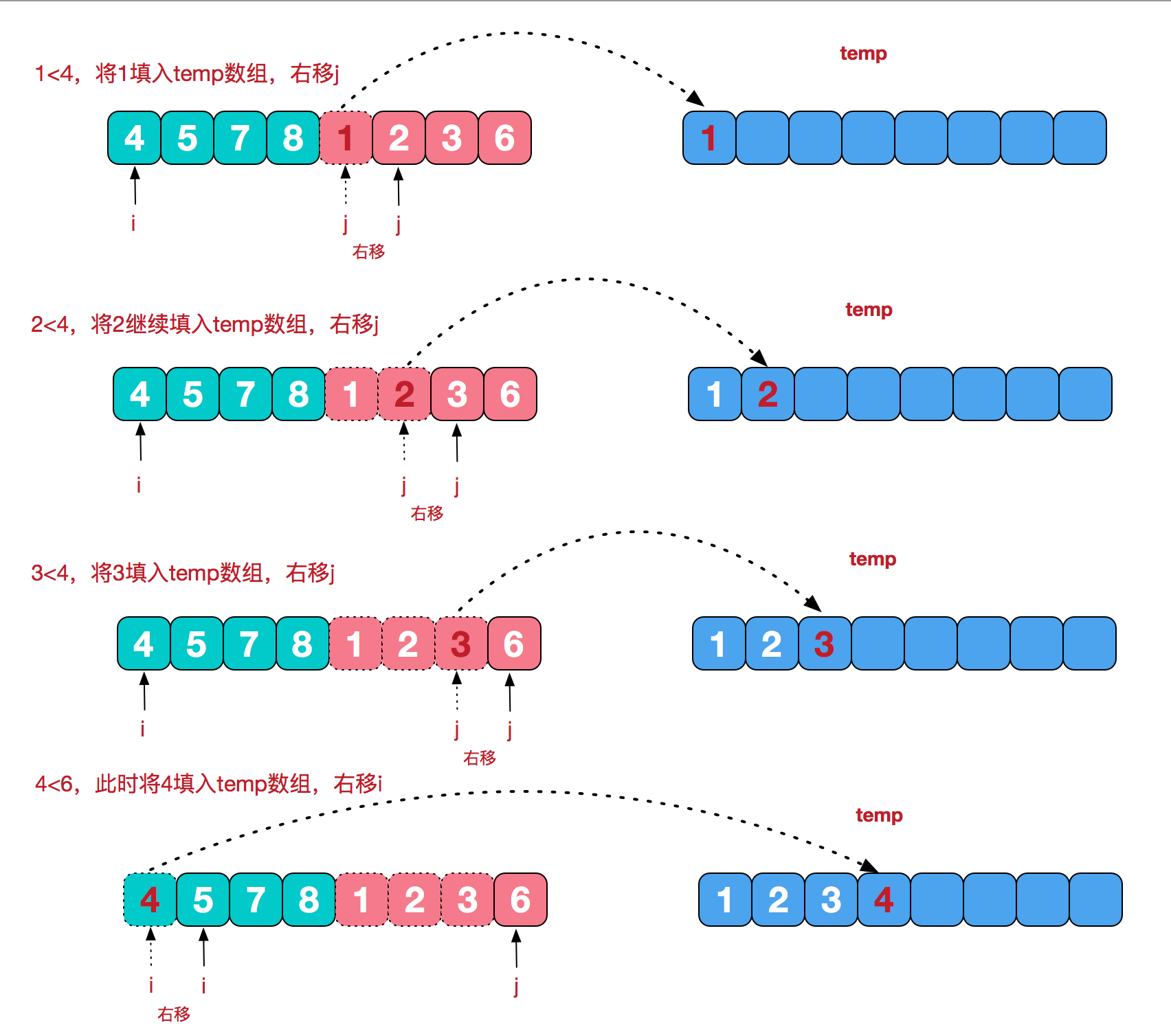
归并排序(逆序数)——P2612 归并排序
快排在分的时候做了很多工作,而归并就是相反,归并在分的时候按照数量均匀分,而合并时候已经是两两有序的进行合并的,因为两个有序序列O(n)级别的复杂度即可得到需要的结果。而逆序数在归并排序基础上变形同样也是分治思想求解。
归并排序参考代码
方法一:归并实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n, a[N], tmp[N];
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
// 分(递归)
int mid = l + r >> 1; // 将数组平均分成两个部分
merge_sort(q, l, mid); // 对左半部分进行分治排序
merge_sort(q, mid + 1, r); // 对右半部分进行分治排序
// 治(合并)
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ]; // 可能的左半部分比右半部分多的
while (j <= r) tmp[k ++ ] = q[j ++ ]; // 可能的右半部分比左半部分多的
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
int main()
{
cin >> n;
for(int i = 0; i < n; i++)
cin >> a[i];
merge_sort(a, 0, n-1);
for(int i = 0; i < n; i++)
cout << a[i] << ' ';
return 0;
}
方法二:另辟蹊径
#include<bits/stdc++.h>
using namespace std;
long long n,a[1000005];
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
}
未完————下期继续