一、说明
简单来说,“仿射变换”就是:“线性变换”+“平移”,但这是在笛卡尔坐标下的表现,然而在射影几何中,其中有更合乎逻辑的解释。本文讲仿射映射的定义,以及仿射不变性的特点。
二、仿射映射
2.1 直线上的仿射映射定义
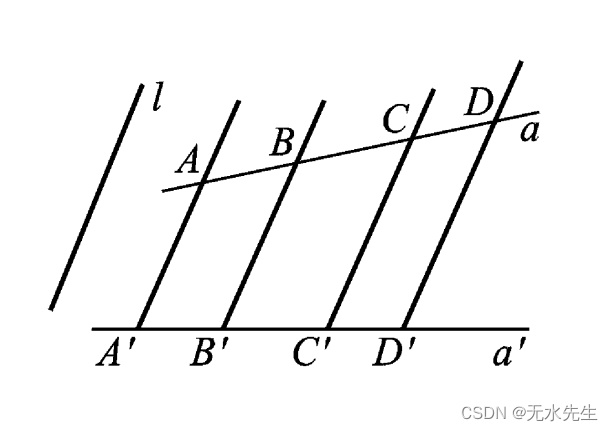
我们来考虑 同一 平面 内直 线 a 到直 线 a′的 平 行射 影 ( 图 1. 1).设 l 为平面上一直线,与 a 及 a′都不平行.通过直线 a 上诸 点 A , B, C, D,…作 l 的平行线,交 a′于 A′, B′, C′, D′,…,这样便定义了直线 a 到直线 a′的一个映射,称为
平行射影或透视仿 射. a 上的点是原象点, a′上的对应点是映象点, l 是平行射影的 方向.记这个透视仿射为 T ,则写 A′= T ( A ),….明显地,平行射 影和方向有关,方向变了,就得出另外的透视仿射.
多重仿射映射
2.2 平面间的仿射映射定义
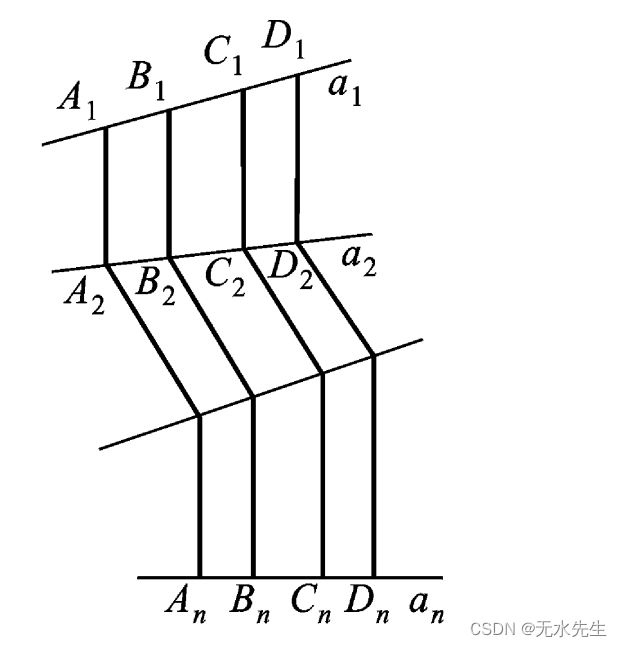
现设同一平面内有 n 条直线 a1
, a
2
,…, a
n
(图 1. 2), 用 T
1 ,T2 ,…, Tn - 1 顺次表示 a1 到 a2 , a2 到 a3 ,…, an - 1 到 an 的透视仿射,经过这一串平行射影, a1 上的点和 an 上的点建立了一个一一对应,称为 a1 到 an 的仿射或仿射变换 T: T = Tn - 1 … T2 T1 , T 称为 T1 , T2 ,…, Tn - 1 按这个顺序的乘积. T ( A1 ) = Tn - 1 … T2 T1 ( A1 ) = Tn - 1 … T2 ( A2 ) = … = An , T( B1 ) = Bn ,等等.注意书写的 顺序跟平行投影的先后顺序是相反的.仿射是由有限回的平行射 影组成的,所以仿射是透视仿射链或平行射影链.透视仿射是最简 仿射.要断定一个仿射是否是透视仿射,只要看原象点和映象点的联线是否都平行
三、仿射不变性性质
- 定理 1 二直线间的平行性是仿射不变性.
- 定义 设 A, B, C 为共线三点,这三点的简比( A B C)定义为 下述有向线段的比: ( A B C) = A C B C.
- C 在线段 A B 上时,简比( A B C) < 0,在 A B 的延长线上时,( A B C) > 0.
- 定理 2 共线三点的简比是仿射不变量.
- 定理 3 两条平行线段之比是仿射不变量.
- 定理 4 一直线上任两线段之比是仿射不变量
-
定理 5 在仿射变换下,任何一对对应三角形面积之比等于 常数.换句话说,任意两个三角形面积之比是仿射不变量.
-
系1 在仿射变换下,任何一对对应多边形面积之比等于常 数.换句话说,任意两个多边形面积之比是仿射不变量。
-
系 2 在仿射变换下,任意两条封闭凸曲线所围成的面积之比是仿射不变量.
四、平面到自身的透视仿射
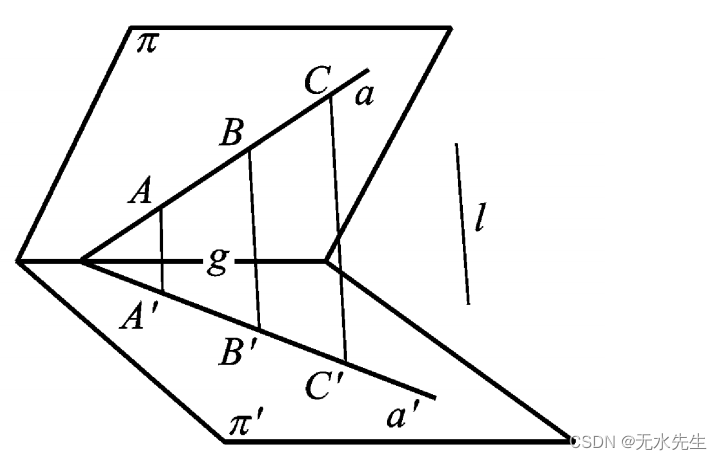
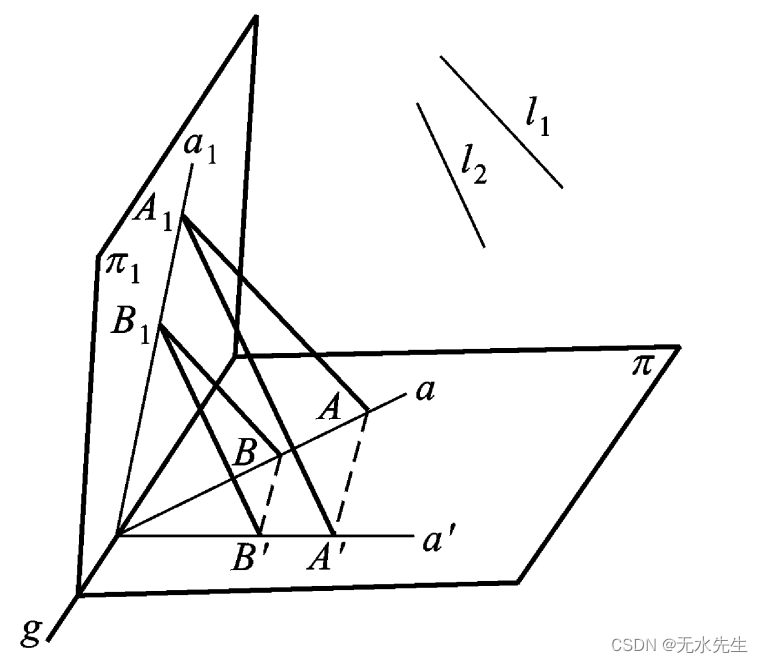
设 T1 为从平面 π到π1
的透视仿射,射影方向为 l1 ; T2 为从 图 平面 π1 到 π的透视仿射,射影方 向为 l2
(图 1. 9). T1 将 π上一点 A 映射为 π1
上的点 A
1
, A A
1 ∥ l
1
; T
2 将 π1
上的点 A1 射回为 π 上一点 A′, A
1 A′∥ l2 . 所以透视 仿射变换 T
1
和 T
2 的乘积 T = T2 T1 将 π上的点 A 变换为本身 上的点 A′.同样,设 T1 ( B) = B1 , T2 ( B1 ) = B′. 于是 仿射变换 T 具有这样的性质, 它将 π上的点 变为 π 上 的 点: T ( A ) = A′, T ( B) = B′;它还将 π上 的直线 a = A B 变为 π 上的 直线 a′= A′B′,即是说, T 保留同素性和结合性.
五、透视仿射和透视映射的关系
5.1 射影透视变换和仿射的关系
将透视映射的射影点拿到无穷远以后,透视映射就蜕变为透视仿射映射。
5.2 仿射函数和线性函数的区别
仿射函数即由由1阶多项式构成的函数,一般形式为 f (x) = A x + b,这里,A 是一个 m×k 矩阵,x 是一个 k 向量,b是一个m向量,实际上反映了一种从 k 维到 m 维的空间映射关系。
设f是一个矢性(值)函数,若它可以表示为f(x1,x2,…,xn)=A1x1+A2x2+…+Anxn+b,其中Ai可以是标量,也可以是矩阵,则称f是仿射函数。
其中的特例是,标性(值)函数f(x)=ax+b,其中a、x、b都是标量。此时严格讲,只有b=0时,仿射函数才可以叫“线性函数”(“正比例”关系)。